Keras构建多输入和多输出模型
在本贴中使用的是从 1985 年到 2018 年美国大学篮球比赛 (US College Basketball tournament games)数据。它属于 NCAA 下面的篮球比赛,始于每年的十一月下旬,跨时四个月,约在三月初左右结束常规赛 (season)。在三月初常规赛季结束后,绝大多数联盟都会取该联盟的前八名球队,交叉配对 (第一名对第八名,第二名对第七名,以此类推)进行新一轮一场定胜负的锦标赛 (tourament)。
读取常规赛和锦标赛的数据,发现前者比后者的数据量大很多,而本贴的目标就是用常规赛数据来训练神经网络再预测锦标赛结果。首先读取数据并查看数据特征。
season = pd.read_csv('season.csv')tourney = pd.read_csv('tourney.csv')
season.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 312178 entries, 0 to 312177
Data columns (total 8 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 season 312178 non-null int64
1 team_1 312178 non-null int64
2 team_2 312178 non-null int64
3 home 312178 non-null int64
4 score_diff 312178 non-null int64
5 score_1 312178 non-null int64
6 score_2 312178 non-null int64
7 won 312178 non-null int64
dtypes: int64(8)
memory usage: 19.1 MBtourney.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 4234 entries, 0 to 4233
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 season 4234 non-null int64
1 team_1 4234 non-null int64
2 team_2 4234 non-null int64
3 home 4234 non-null int64
4 seed_diff 4234 non-null int64
5 score_diff 4234 non-null int64
6 score_1 4234 non-null int64
7 score_2 4234 non-null int64
8 won 4234 non-null int64
dtypes: int64(9)
memory usage: 297.8 KB前者有 8 个特征,而后者有 9 个特征,多了一个 seed_diff。球队打完常规赛后会排名,按照名次来打锦标赛,这个 seed_diff 就是两队的排名差。训练一个模型,输入是排名差,输出是比分差 (score_diff)。
所有排名以 1 到 16 来表示,那么排名差的范围从 -15 到 15
比分差大概范围从 -50 到 50
打印出锦标赛数据的前五行,发现队伍的字符串都由整数来编码了。再者该数据是对称的,比如行 0 和 4,是队伍 288 和 73 的一场比赛结果,但分别把 288 当作 team_1 和 team_2,因此两行中的 seed_diff 和 score_diff 都互为相反数。
tourney.head()
有了 NCAA 数据,在接下三节里构建简单模型、多输入模型 (multi-input model) 和多输出模型 (multi-output model)。
2.1
知识回顾
虽然 Keras 构建的都是神经网络,但也能构建线性回归和对率回归模型,因为两种模型都是神经网络的特殊形式,即不带隐含层。再精简一步,对于单变量线性回归和对率回归模型,那么该神经网络就只有一个输入和一个输出,示意图如下:

上图中 是输入, 是激活函数,对于线性回归 ;对于对率回归 ,因此 将输入转换成输出。从功能上讲,Keras 将输入和输出类比成张量 (tensor),将函数类比成层 (layer),将输入经过若干层得到输出的流程类比成模型 (model)。结合 Keras 中定义的示意图如下:

根据上图在牢记以下四点便可以轻松在 Keras 中构建模型了:
Input()中形状参数代表输入维度,Input((1,))指输入张量是一维标量
Dense()中参数代表输出维数,Dense(1)指输出一个标量
层函数作用在张量上并返回另一个张量,这两个张量分别称为该层的输入张量和输出张量
构建模型只需将最初的输入张量和最终的输出张量“捆绑”在一起即可
趁热打铁用代码巩固以上知识,首先引入需要的模块,Input 创建输入张量,Dense 创建层,Model 构建模型,plot_model 可视模型。
from keras.layers import Input, Densefrom keras.models import Modelfrom keras.utils import plot_model
用 Input()创建输入张量,检查其类型是 Tensor,形状是 (None, 1),None 指的是每批训练的数据个数,通常在训练时 fit() 函数中 batch_size 参数决定。
input_tensor = Input(shape=(1,))print(type(input_tensor), '\n', input_tensor)
'tensorflow.python.framework.ops.Tensor'>
Tensor("input_1:0", shape=(None, 1), dtype=float32) 用 Dense()创建输出层,检查其类型是 layers,是层对象。
output_layer = Dense(1)print(type(output_layer), '\n', output_layer)
'tensorflow.python.keras.layers.core.Dense'>
python.keras.layers.core.Dense object at 0x7fb1df536e80> 将输出张量传入层得到输出张量,检查其类型是 Tensor,形状是 (None,
1)。
output_tensor = output_layer(input_tensor)print(type(output_tensor), '\n', output_tensor)
'tensorflow.python.framework.ops.Tensor'>
Tensor("dense/BiasAdd:0", shape=(None, 1), dtype=float32) 用 Model()创建模型,将输入和输出张量“绑在”一起。检查其类型是 Functional,是函数对象。
model = Model(input_tensor, output_tensor)print(type(model), '\n', model)
'tensorflow.python.keras.engine.functional.Functional'>
python.keras.engine.functional.Functional object at 0x7fb1df5591d0> 模型创建完后,用 plot_model()函数可视化网络结构。
plot_model(model, to_file='model.png')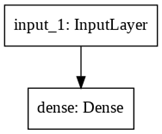
还可用 .summary()函数来打出网络每层信息,以及参数总数。
model.summary()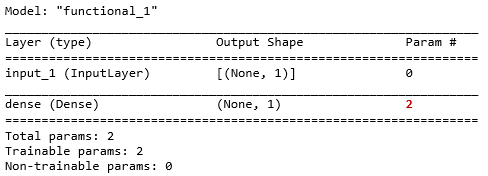
根据上面信息发现 Input 也当成一层了,之前提到过层其实类比函数,但输入只是一个张量,如真要当成函数,那么对应的就是个自身函数 f(x) = x。在 Dense 层对应的参数是 2,因为多了一个偏置项,但这些细节没有在上面可视图中体现。补充完细节的示意图如下:

最后用 .compile()函数来编译模型,在函数中设定优化器、损失函数和监控指标等参数。
model.compile(optimizer='adam', loss='mae', metrics=['accuracy'])2.2
线性回归模型
把 2010 年之前的锦标赛当作训练集,2011年之后的锦标赛当作测试集。构建-编译-拟合-评估走一波。
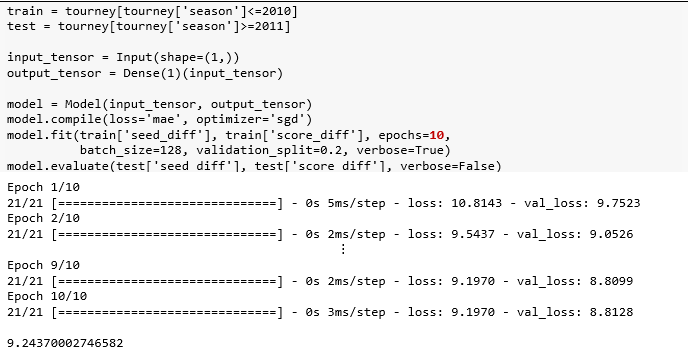
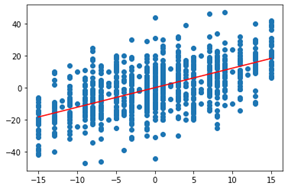
该模型是单变量线性回归 y = wx + b,顺着模型调出最后一层再使用 get_weights() 方法打印权重,并可视化拟合效果。
w, b = model.layers[1].get_weights()print(w, b)
[[1.2168913]] [0.00527138]plt.scatter(test['seed_diff'], test['score_diff'])x = np.linspace(test['seed_diff'].min(),test['seed_diff'].max(), 200)plt.plot( x, w[0]*x+b, color='red' );
2.3
对率回归模型
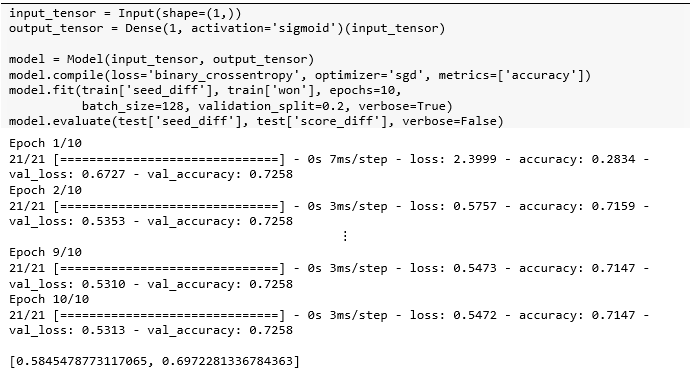
该模型是单变量对率回归 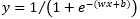 ,调出最后一层再使用 get_weights() 方法打印权重,并可视化预测结果。标签中的胜负各占一半,但该极简模型预测出来的胜比负略多一些。
,调出最后一层再使用 get_weights() 方法打印权重,并可视化预测结果。标签中的胜负各占一半,但该极简模型预测出来的胜比负略多一些。
w, b = model.layers[1].get_weights()print(w, b)
[[0.16914853]] [0.00290928]results = test[['seed_diff','won']]preds = model.predict(test['seed_diff'])a = np.zeros(preds.shape, dtype=int)a[preds>=0.5] = 1results['pred_won'] = aplt.figure( figsize=(8,4), dpi=100 )plt.subplot(1,2,1)sns.countplot(data=results, x='won')plt.subplot(1,2,2)sns.countplot(data=results, x='pred_won')

上节只用了 seed_diff 一个特征来构建模型,本节用队伍 ID team_1 和 team_2 和主客场 home 来建模。首先引入必要的模块。
from keras.layers import Input, Dense,Embedding, Flatten, Substract, Concatenate
特征 team_1 和 team_2 的值类型虽然是整数,但本质上是个类别型标签 (categorical label),强队对应的 team 值不见得大,弱队对应的 team 值也不见得小,因此不能将它们当整数用。通常使用独热编码(one-hot encoding) 向量化,但有两个缺点:一是向量之间缺乏有意义的关系,二是总共有10000 多支球队而向量过于稀疏。解决这些问题的方法是使用嵌入层,将高维稀疏向量转换为低维稠密向量。
具体而言,构建一个嵌入层代表团队实力 (team strengh),输入维度 input_dim 就是所有队伍个数,输出维度 output_dim为 1,即用一个标量代表团队实力值 (类比 word2vec 中用 300 维的向量代表一个词)。每个输入长度 input_length 为 1,因为 team_1 的值就是一个标量。

嵌入层本质就是查找表 (lookup table),将输入team ID 和团队实力一一对应,接着将所有球队的实力值打平作为“团队实力模型”的输出。

嵌入层首先用独热编码将 Team ID 装成向量,再通过查找表矩阵(元素是训练出来的) 获取权重,最后打平拼接起来。整套流程的可视图如下。

球队个数为 10,888,由于输出维度是 1,那么对应的参数也是 10,888。
team_strength_model.summary()
plot_model(team_strength_model)
数据中有 team_1 和 team_2,如果任何一对球队互相比赛,模型就可以预测得分,即便这两队之前从未参加过比赛。此外无论是主队还是客队,它们强度等级相同。为此,可使用一个共享层,即重用上面模型team_strength_model()。

了解了每队的实力后,有两种处理方式:
相减层 (Substract Layer)
拼接层 (Concatenate Layer)
先看相减层,对 team_1 和 team_2 实力相减来确定赢得比赛的队。这有点像比赛委员会使用的种子,也是衡量团队实力的标准。但是之后将不使用种子差异来预测得分差异,而是使用自己的团队实力模型差异来预测得分差异。
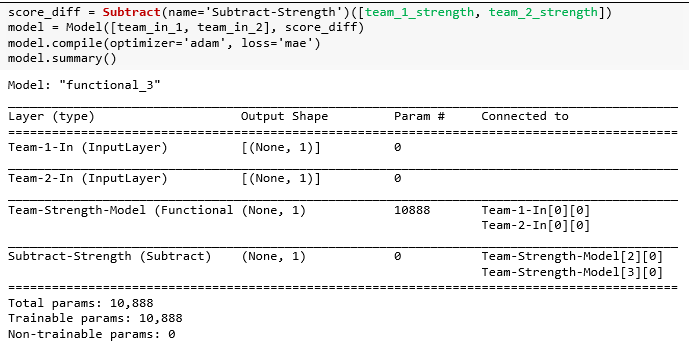
可视化该模型,发现 Team-1-In 和Team-2-In 共享之前构建好的“团队实力”模型,得出的两组实力值在“相减层”中做差值。
plot_model(model)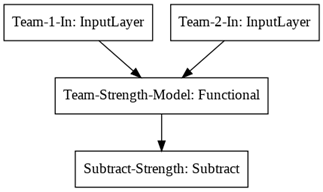
现在有两个输入,将它们传入列表作为 model.fit() 的参数。

众所周知篮球中有一个有据可查的主队优势,因此将向模型中添加新的输入以捕获这种效果。该模型将具有三个特征 team_1,team_2 和h ome,前两个用嵌入层转成“团队实力”,而 home 是一个二进制变量,如果 team_1 作为主队比赛为 1;否则为 0。
使用拼接层将两队的实力、主客场结合在一起,然后将结果传递给稠密层。

可视化该模型,发现 Team-1-In 和 Team-2-In 共享之前构建好的“团队实力”模型,得出的两组实力值和额外的主客场在“拼接层”中做合并,最后连接一个稠密层。
plot_model(model)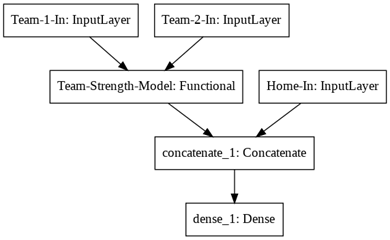
现在有三个输入,将它们传入列表作为 model.fit() 的参数,和上面两个输入的代码比较,唯一的区别就是列表从包含两个元素增加到三个元素。由此可见 Keras 写起来真的非常灵活和优雅。

打印嵌入层 (layers[2]) 和稠密层 (layers[5]) 的参数,具体索引哪层可参考 model.summary()的信息。

嵌入层中的参数有 10,888 个,而稠密层中的参数有 4 个,包括 3 个 w 和 1 个 b。
之前使用常规赛模型对锦标赛数据进行了预测,效果不错,因此可将常规赛模型预测作为锦标赛模型的输入,能进一步提高模型预测效果,这是“模型堆叠”的一种形式。首先用常规赛季模型为基础,并根据锦标赛数据进行预测,将此预测作为新列添加到锦标赛数据中。
tourney['pred'] = model.predict([tourney['team_1'],tourney['team_2'],tourney['home']])
该模型的输入是锦标赛数据中 'seed_diff' 和'pred' 两列,而输出是得分差异。
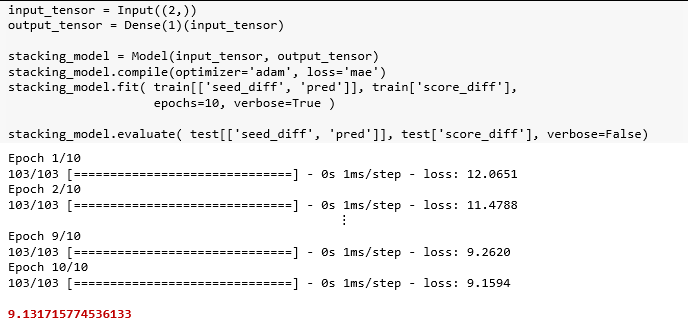
在测试集得到的结果 9.13 比之前的 10.09 更好一些。
本节将构建具有多个输出的神经网络,这些神经网络可用于
解决具有多个目标的回归问题。
同时解决回归问题和分类问题。
用锦标赛数据来建立一个做两个预测的模型,输入是两队的种子差异,输出它们得分。注意代码中褐色部分,为什么使用这样的学习率 lr、期数epochs 和批大小 batch_size?通过调节超参数,在 Keras 下篇后会细讲。
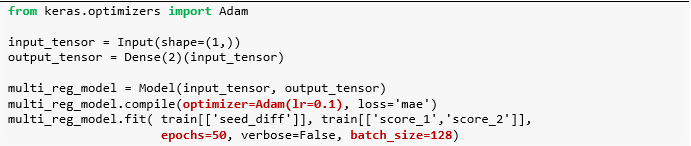
由于该模型是单输入双输出,那么两个回归模型都有各自的 w 和 b,参数一共有 4 个。
multi_reg_model.summary()
打印参数发现两队得分的模型为
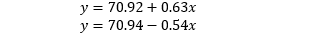
由于 x 代表的是种子差,其均值为 0,那么两队得分的均值大概就是 70.9。对于一队,排名差距增加一个单位,分数可增加 0.63 分,对于二队,排名差距增加一个单位 (二队增加相当于一队减少),分数可增加 0.54 分。
w, b = multi_reg_model.layers[-1].get_weights()print(w, w.shape)print(b, b.shape)
[[ 0.62823033 -0.54407144]] (1, 2)
[70.91642 70.94076] (2,)计算真实种子差的均值得到是 0,因为该数据是完全对称的,两队一场比赛分为两条数据记录。两队得分的均值为 71.8,跟上面模型学到的 70.9 也很接近。
train[['seed_diff','score_1','score_2']].mean()seed_diff 0.000000
score_1 71.786711
score_2 71.786711
dtype: float64接着将创建另一种类型的两输出模型。 它不仅能预测得分差异,还然后预测一队赢得比赛的概率。该模型非常酷,它将同时进行分类和回归。
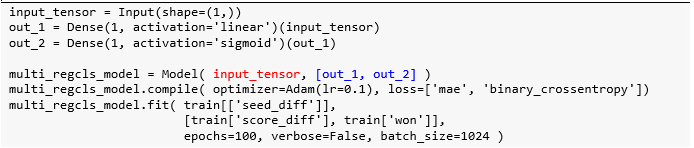
由于该模型是单输入双输出,那么线性回归和对率回归模型都有各自的 w 和 b,参数一共有 4 个。
multi_regcls_model.summary()
plot_model(multi_regcls_model)
由上图可知用于对率回归的层紧接着用于线性回归的层,因此分别从 layers[1] 和 layers[2] 获取对应的参数。

用上面的结果可看出两队种子每相差一位,比分就相差 1.21 分。使用 tf.keras 中的 sigmoid() 函数,将训练好的权重和偏置带入,得到当一队比二队多 1 分的时候,一队的胜率为 0.53;当一队比二队少 10 分的时候,一队的胜率为 0.21。

总结:在本贴中我们复习了 Keras 中构建、编译、拟合和评估模型的步骤,并从简单模型开始讲解,到多输入模型 (介绍了嵌入层、共享层、合并层和堆积法等知识点),到多输出模型 (同时做两个回归、同时做回归和分类)。
Stay Tuned!