机器学习中的优化算法!
每日干货 & 每月组队学习,不错过
作者:李祖贤,Datawhale高校群成员,深圳大学
1.1 最速下降法的原理
 ,我们想求
,我们想求 处使得
处使得  下降最快的方向。由上一章可知:这个方向应首先满足下降条件
下降最快的方向。由上一章可知:这个方向应首先满足下降条件 。虽然下降方向有无穷多个,但是根据Cauchy-Schwarz不等式:
。虽然下降方向有无穷多个,但是根据Cauchy-Schwarz不等式: 当且仅当
当且仅当 时等式成立,
时等式成立, 达到最小。由于在
达到最小。由于在 方向上要考虑步长,故取
方向上要考虑步长,故取 为负梯度方向:
为负梯度方向: 。
。

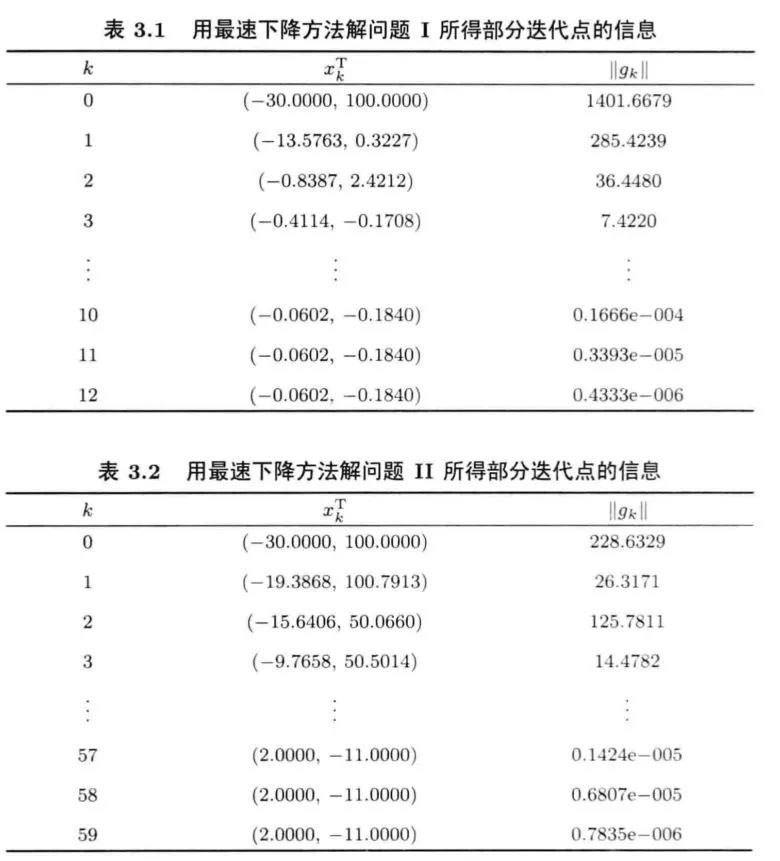
我们从上面可以看到,不同的G矩阵使用最速下降法的迭代速度有明显的差异,原因在后文给出。
1.2 最速下降法的收敛速度
1.2.1 收敛性
向量u在矩阵G度量下的范数:
矩阵G度量下的Cauchy-Schwarz不等式:

Kantorovich不等式:

1.2.3 收敛速度的上界


由此可知,最速下降法的收敛速度是线性的,这个速度依赖于G的最大最小特征值。
我们假设G和b产生了微小扰动变成了 ,正定二次函数:
,正定二次函数:  的导函数方程相应变成了
的导函数方程相应变成了  ,方程的解记为
,方程的解记为 ,其中
,其中 非奇异,
非奇异, 满足
满足 非零。那么:
非零。那么:

条件数与范数有关,因此是G的相对误差与b的相对误差之和的放大倍数。若矩阵G的条件数很大,扰动对解的影响很大,我们称这个问题是病态的,或G是病态的。若矩阵G的条件数不大,扰动对解的影响程度不大,我们就成这样的问题是良性的,或G是良性的。
因此:

这说明最速下降法的收敛速度依赖G的条件数,当G的条件数接近于1时, 接近于0,最速下降法的收敛速度接近于超线性收敛;而当G的条件数很大时,
接近于0,最速下降法的收敛速度接近于超线性收敛;而当G的条件数很大时, 接近于1,则收敛很慢。
接近于1,则收敛很慢。


缺点:
收敛慢:线性收敛。
Zigzag现象(收敛慢的原因):若迭代步
 是
是  的精确最小点,则
的精确最小点,则 ,因此:
,因此:  ,也就是上一步的方向与下一步的方向垂直。
,也就是上一步的方向与下一步的方向垂直。
没有二次终止性:即不具备对于任意的正定二次函数,从任意点出发,都可以经过有限步迭代取得极小值的性质。
二、Newton方法
2.1 基本Newton方法
设 具有连续二阶偏导数,当前迭代点是
具有连续二阶偏导数,当前迭代点是 。
。 在
在  的泰勒展开为:
的泰勒展开为:

 。在点
。在点 的邻域内,用二次函数
的邻域内,用二次函数 去近似
去近似 ,求解问题
,求解问题 。
。 正定,则迭代方向
正定,则迭代方向 为问题的唯一解。我们称
为问题的唯一解。我们称 为Newton方向。(Hesse的逆矩阵度量下的最速下降法)
为Newton方向。(Hesse的逆矩阵度量下的最速下降法)我们来看看牛顿迭代的方向和梯度下降的方向有什么不一样?(黑色为牛顿下降方向,红色为负梯度下降方向)

下面我们用一个具体的例子来看看牛顿迭代法的效果:


(3)迭代过程可能会出现奇异矩阵或者病态,以至于求逆很困难,导致迭代失败。
当
 的特征值
的特征值 ,
, 求不出来。
求不出来。当  的特征值
的特征值
不一定小于0,牛顿方向未必是下降方向。
(4)每一步迭代需要计算Hesse矩阵,即计算n(n+1)/2个二阶偏导数,相当于求解一个线性方程组,计算量为O( )
)
2.2 阻尼Newton方法
为了改善基本Newton方法的局部收敛准则,我们采用带一维线搜索的的Newton方法,即

其中 是一维搜索的结果,该方法叫做阻尼Newton方法。此方法能保证对正定矩阵
是一维搜索的结果,该方法叫做阻尼Newton方法。此方法能保证对正定矩阵 ,
, 单调下降;即使
单调下降;即使  离x稍远,由该方法产生的点列
离x稍远,由该方法产生的点列 仍能收敛到
仍能收敛到 。(对严格凸函数具有全局收敛性)
。(对严格凸函数具有全局收敛性)
2.3 混合方法
 几乎正交的情形。为了解决这个问题,我们可以采用基本Newton方法与最速下降法相互混合的方式。
几乎正交的情形。为了解决这个问题,我们可以采用基本Newton方法与最速下降法相互混合的方式。 奇异或者
奇异或者 与
与 几乎正交时,采用负梯度方向;在
几乎正交时,采用负梯度方向;在 负定,但是
负定,但是 存在时,取
存在时,取 。
。
2.4 LM方法
 奇异、不正定等情况的一个最简单有效的方法,它是指求解
奇异、不正定等情况的一个最简单有效的方法,它是指求解  来确定迭代方向的Newton型方法,这里的
来确定迭代方向的Newton型方法,这里的 是单位阵。显然,若
是单位阵。显然,若 足够大,可以保证
足够大,可以保证 正定。
正定。(1)  的大小对于方向的影响:
的大小对于方向的影响:
当
 很小,求出的步长偏向于Newton方向。
很小,求出的步长偏向于Newton方向。当  很大,求出的步长则偏向于负梯度方向。
很大,求出的步长则偏向于负梯度方向。
(2)当 不正定时,可以简单取
不正定时,可以简单取
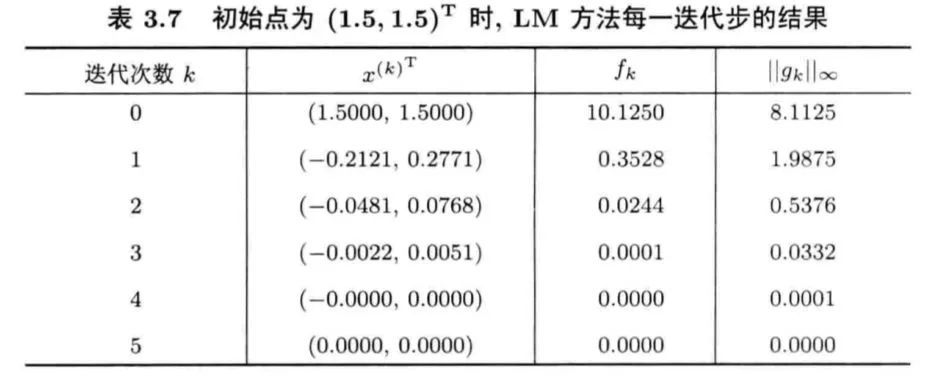
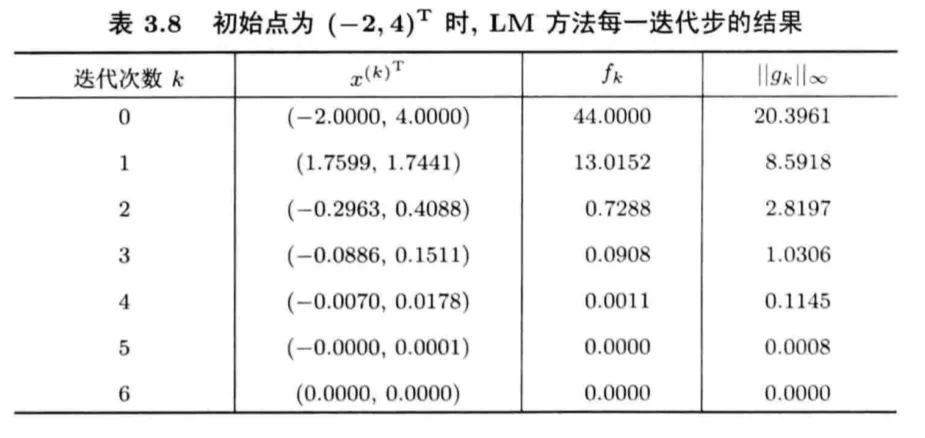

三、拟牛顿方法
Newton方法的优缺点:
(1)当初始点接近极小点时,迭代序列收敛于极小点,并且收敛很快(二阶收敛);
(2)当初始点不接近极小点时,迭代序列容易收敛到鞍点或者极大点(局部收敛性而不是全局收敛)。
(3)迭代过程可能会出现奇异矩阵或者病态,以至于求逆很困难,导致迭代失败。
当
 的特征值
的特征值 ,
, 求不出来。
求不出来。当
 的特征值
的特征值 ,
, 
不一定小于0,牛顿方向未必是下降方向。
 )
)为此,我们考虑构造一种方法,她既不需要计算二阶偏导数,又有较快的收敛速度。
3.1 拟牛顿条件
 ,已知条件为
,已知条件为 ,我们使用拉格朗日中值定理:
,我们使用拉格朗日中值定理: 
我们可以使用矩阵 似
似 得到
得到  n个方程,n(n+1)/2个变量。
n个方程,n(n+1)/2个变量。
 得到:
得到: 
因此拟牛顿条件为:


在上述算法中,初始矩阵 一般取单位矩阵,第一步迭代方向取为负梯度方向。
一般取单位矩阵,第一步迭代方向取为负梯度方向。
那么,算法的核心就是怎么由 去修正
去修正 ,即
,即 ,而
,而 的取法是多种多样的,但是他应该具有简单、计算量小、有效的特点。
的取法是多种多样的,但是他应该具有简单、计算量小、有效的特点。
3.2 拟牛顿方法的修正公式
3.2.1 对称秩1公式
 为对称秩1矩阵,即有
为对称秩1矩阵,即有 。
。将 代入拟牛顿方程
代入拟牛顿方程  得到:
得到:

 。
。 是一个数,因此u与
是一个数,因此u与 共线,从而存在
共线,从而存在 使得:
使得: 。
。将 代入
代入 得到
得到

因此 ,由此得到
,由此得到
 .
.
如果我们想将 换成等价的
换成等价的 ,则需要用到SMW公式:
,则需要用到SMW公式:

最终得到对称秩1公式:

3.2.2 对称秩2公式
 为对称秩2矩阵,即
为对称秩2矩阵,即 ,其中
,其中  待定。
待定。将 代入
代入 中,得到
中,得到 的修正公式
的修正公式 。
。
(1)DFP方法
 中,化简为
中,化简为 
由于 的选择不是唯一的,为了计算方便,我们选择:
的选择不是唯一的,为了计算方便,我们选择:

代入公式中可得  ,得到DFP公式:
,得到DFP公式:


(2)BFGS公式(对偶)
 的修正公式:
的修正公式:  用相同的推断实现:
用相同的推断实现:
根据SMW公式:

(3)Broyden族公式

3.3 三种拟牛顿方法的对比试验
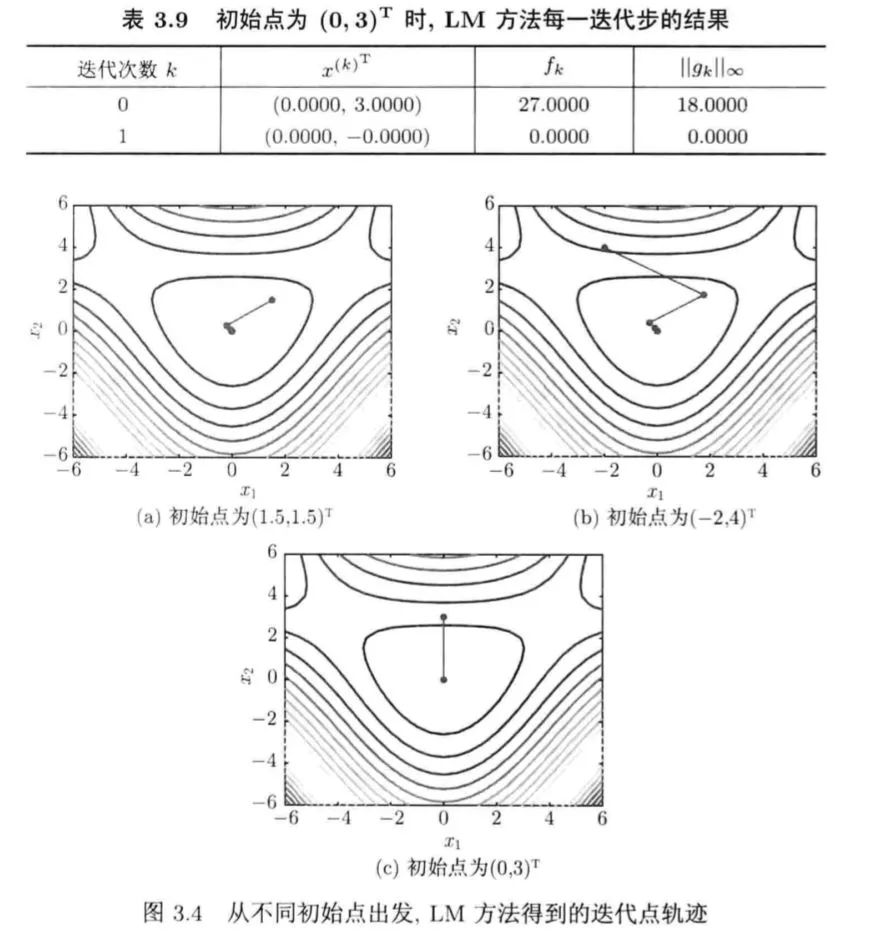
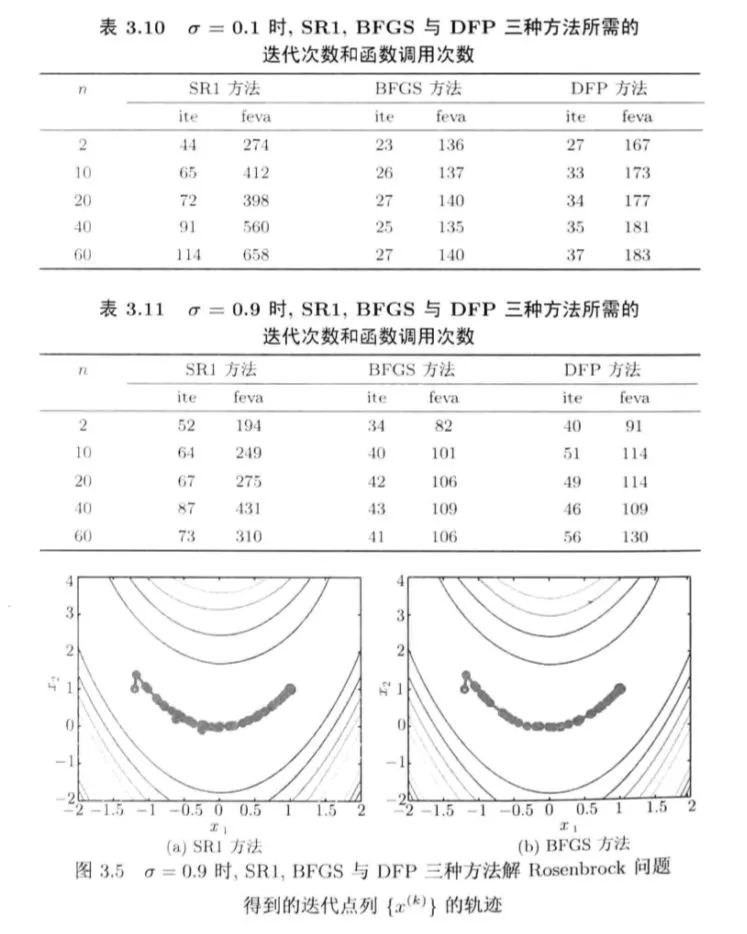
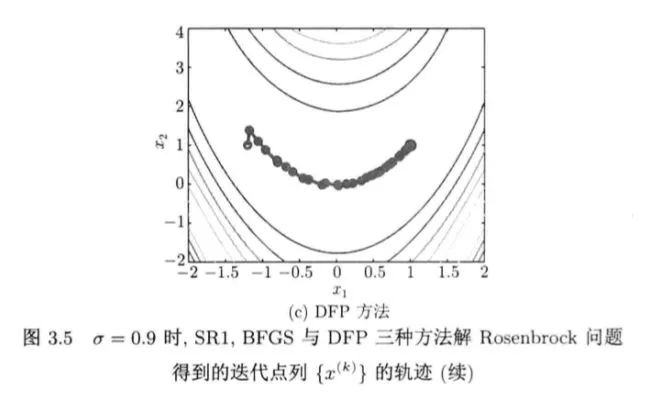
(1)扩展Rosenbrock问题
(BFGS与DFP差异不大,SR1差些)(迭代次数与函数调用次数)
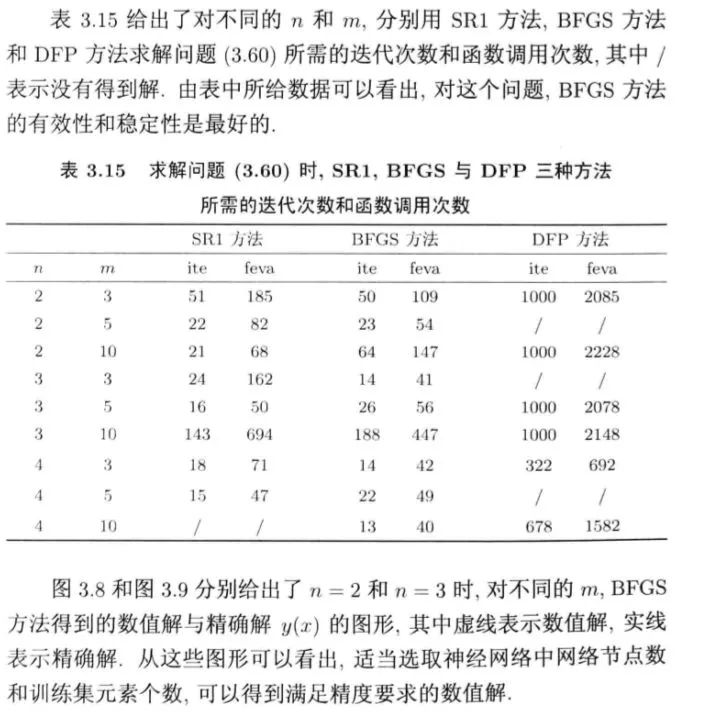
(2)由人工神经网络解微分方程的问题:


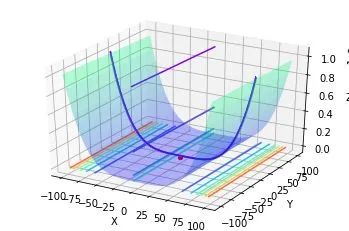
四、使用牛顿法优化Rosenbrock函数实例(基于python)

import numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport time%matplotlib inlinefrom mpl_toolkits.mplot3d import Axes3Dclass Rosenbrock():def __init__(self):self.x1 = np.arange(-100, 100, 0.0001)self.x2 = np.arange(-100, 100, 0.0001)#self.x1, self.x2 = np.meshgrid(self.x1, self.x2)self.a = 1self.b = 1self.newton_times = 1000self.answers = []self.min_answer_z = []# 准备数据def data(self):z = np.square(self.a - self.x1) + self.b * np.square(self.x2 - np.square(self.x1))#print(z.shape)return z# 随机牛顿def snt(self,x1,x2,z,alpha):rand_init = np.random.randint(0,z.shape[0])x1_init,x2_init,z_init = x1[rand_init],x2[rand_init],z[rand_init]x_0 =np.array([x1_init,x2_init]).reshape((-1,1))#print(x_0)for i in range(self.newton_times):x_i = x_0 - np.matmul(np.linalg.inv(np.array([[12*x2_init**2-4*x2_init+2,-4*x1_init],[-4*x1_init,2]])),np.array([4*x1_init**3-4*x1_init*x2_init+2*x1_init-2,-2*x1_init**2+2*x2_init]).reshape((-1,1)))x_0 = x_ix1_init = x_0[0,0]x2_init = x_0[1,0]answer = x_0return answer# 绘图def plot_data(self,min_x1,min_x2,min_z):x1 = np.arange(-100, 100, 0.1)x2 = np.arange(-100, 100, 0.1)x1, x2 = np.meshgrid(x1, x2)a = 1b = 1z = np.square(a - x1) + b * np.square(x2 - np.square(x1))fig4 = plt.figure()ax4 = plt.axes(projection='3d')ax4.plot_surface(x1, x2, z, alpha=0.3, cmap='winter') # 生成表面, alpha 用于控制透明度ax4.contour(x1, x2, z, zdir='z', offset=-3, cmap="rainbow") # 生成z方向投影,投到x-y平面ax4.contour(x1, x2, z, zdir='x', offset=-6, cmap="rainbow") # 生成x方向投影,投到y-z平面ax4.contour(x1, x2, z, zdir='y', offset=6, cmap="rainbow") # 生成y方向投影,投到x-z平面ax4.contourf(x1, x2, z, zdir='y', offset=6, cmap="rainbow") # 生成y方向投影填充,投到x-z平面,contourf()函数ax4.scatter(min_x1,min_x2,min_z,c='r')# 设定显示范围ax4.set_xlabel('X')ax4.set_ylabel('Y')ax4.set_zlabel('Z')plt.show()# 开始def start(self):times = int(input("请输入需要随机优化的次数:"))alpha = float(input("请输入随机优化的步长"))z = self.data()start_time = time.time()for i in range(times):answer = self.snt(self.x1,self.x2,z,alpha)self.answers.append(answer)min_answer = np.array(self.answers)for i in range(times):self.min_answer_z.append((1-min_answer[i,0,0])**2+(min_answer[i,1,0]-min_answer[i,0,0]**2)**2)optimal_z = np.min(np.array(self.min_answer_z))optimal_z_index = np.argmin(np.array(self.min_answer_z))optimal_x1,optimal_x2 = min_answer[optimal_z_index,0,0],min_answer[optimal_z_index,1,0]end_time = time.time()running_time = end_time-start_timeprint("优化的时间:%.2f秒!" % running_time)self.plot_data(optimal_x1,optimal_x2,optimal_z)if __name__ == '__main__':snt = Rosenbrock()snt.start()
请输入需要随机优化的次数:100
优化的时间:8.10秒!
本文电子版 后台回复 优化算法 获取
“整理不易,点赞三连↓
