机器学习小知识: 图解熵、交叉熵和 KL-散度

1什么是熵?
首先,本文指的熵是指信息熵。想要明白熵的确切含义,先让我们了解一下信息论的一些基础知识。在这个数字时代,信息由位(即比特,由 0 和 1)组成。在通信时,有些位是有用的,有些是冗余的,有些是错误,依此类推。当我们传达信息时,我们希望向收件人发送尽可能多的有用信息。
在 Claude Shannon 的论文《通信的数学理论》(1948)中,他指出,传输 1 比特的信息意味着将接收者的不确定性降低 2 倍。
让我们来看看他说的意思。例如,考虑一个天气状况随机的地方,每天可能有 50% 的机率是晴天或阴雨。
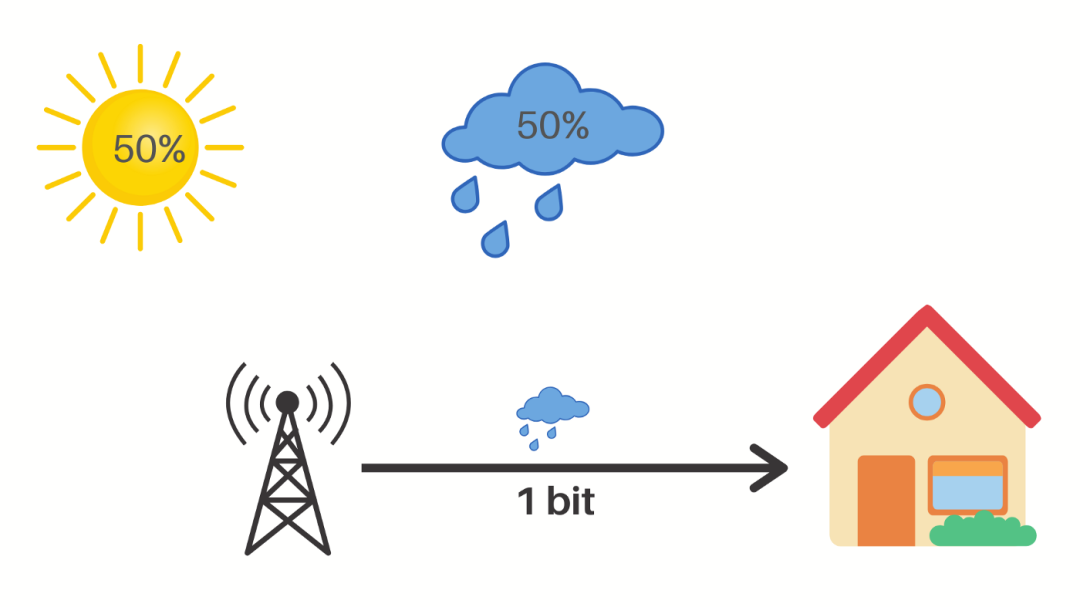
现在,如果气象站告诉你明天要下雨,那么他们将不确定性降低了 2 倍。起初,有两种可能,但在收到气象站的信息后,就只有一种可能了。在这里,气象站向我们发送了一点点有用的信息,无论他们如何编码这些信息,这都是事实。
即使发送的信息是多雨(Rainy),并且每个字符占用一个字节,消息总的大小也相当于 40 比特,但是它们仍然只传达了 1 比特的有用信息。
假设天气有 8 种可能的状态,所有可能性都相同。
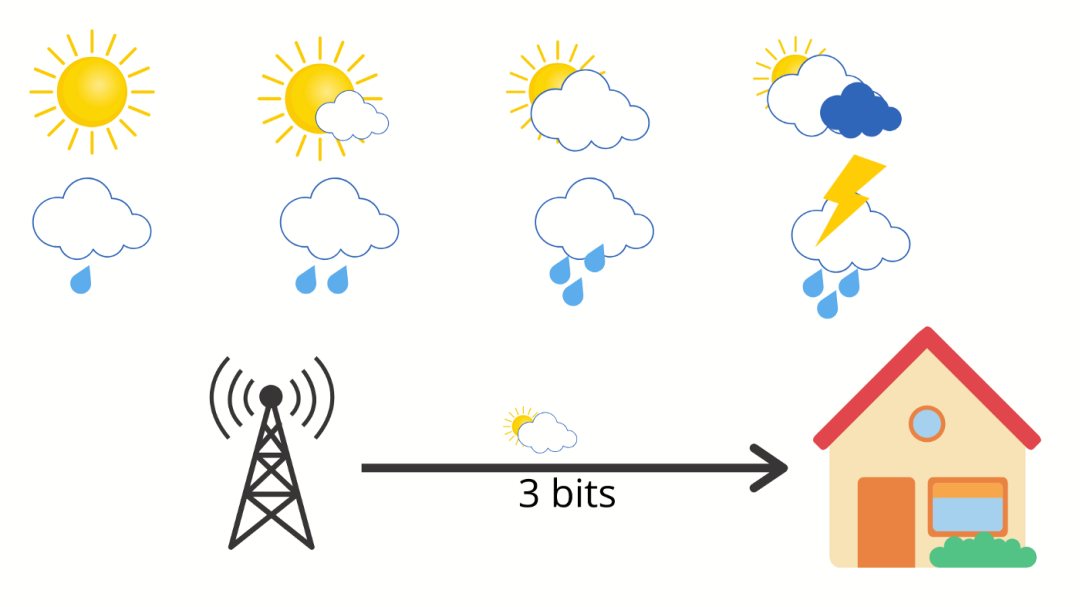
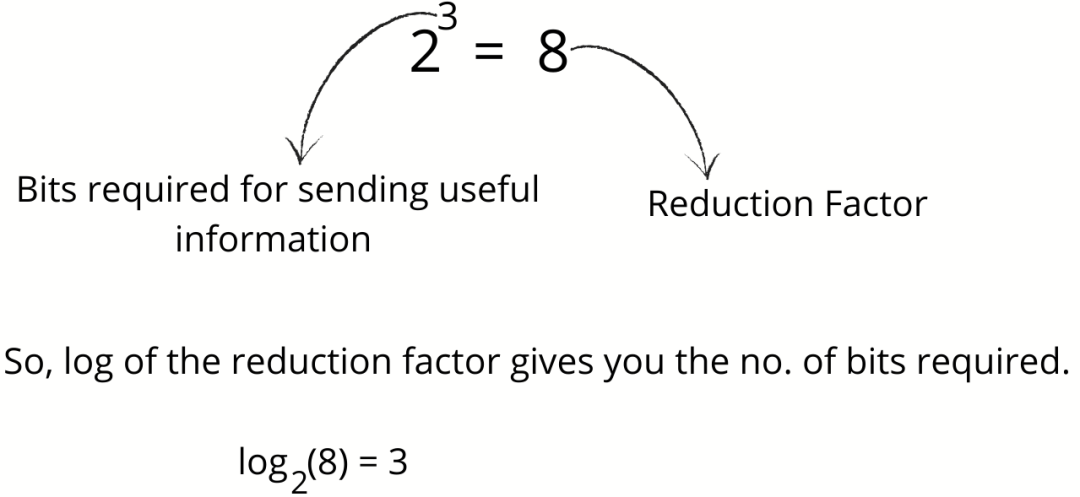
现在,当气象站为你提供第二天的天气时,它们会将不确定性降低了 8 倍。由于每个事件的发生机率为 1/8,因此降低因子为 8。
但是,如果不同天气的可能性不一样该怎么办呢?
假设有 75% 的概率是晴天,25% 的概率是下雨。
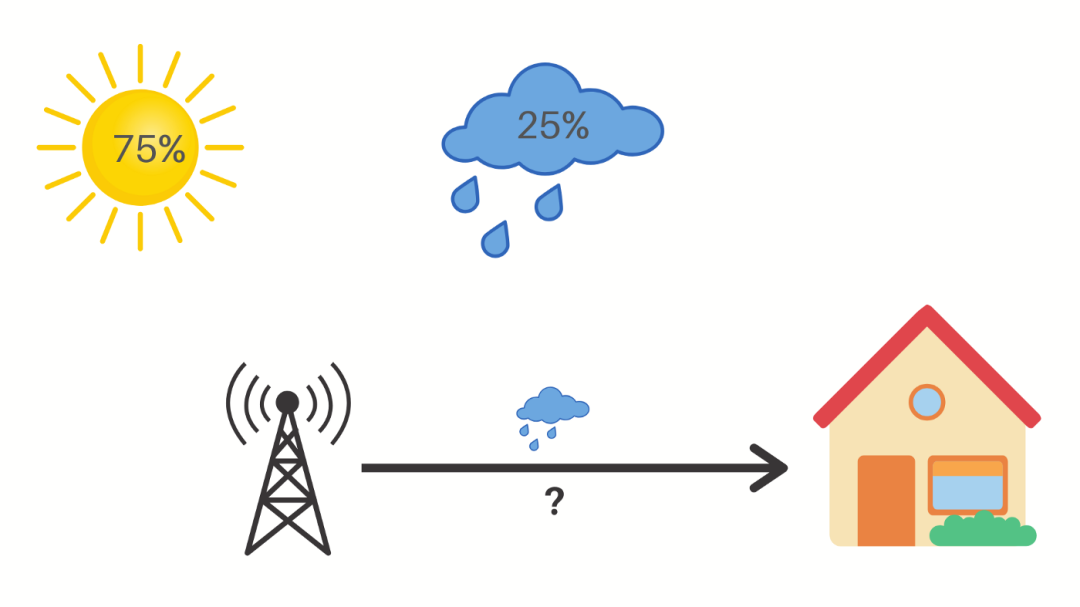
现在,如果气象站说第二天要下雨,那么不确定性就会降低 4 倍,即 2 个比特信息。减少的不确定性是事件概率的倒数。在这种情况下,25% 的倒数是 4,以 2 为底的
解读
原来凭空猜下雨,你只有 1/4 把握,得到天气预报后现在的把握是 1 了。确定性提升到 4 倍,或者说不确定性降低到 4 倍。 原来猜晴天,你有 3/4 把握,得到天气预报后现在的把握是 1 了。确定性提升到 4/3 倍,或者说不确定性降低到 4/3 倍。
2信息熵
我们经常会说,某个新闻的信息量好大。那么这个信息量到底怎么定义呢?所含的文字?所表达的内容?貌似并不好定义。
可以这么来理解,对某个事件由不确定到确定就得到了所谓的信息量,那么如何来量化它呢?即这个信息量到底有多大呢?这个就需要对不确定到确定这个转化作量化了。首先看看怎么量化不确定性。通过前文我们知道,事件概率越大,不确定性自然就越小,再结合事件是独立的这个前提。信息量应该满足下面这些条件,
信息量跟事件的概率值成反比,即 。概率越大的事件确定性越大,因此由不确定到确定的转化所含的信息量越小。 两个独立事件所对应的信息量应等于各自信息量之和,因为相互不影响,所谓的可加性,即 。
满足这两个条件的常见函数有吗?答案是肯定的,比如
这个正是 Shannon 采用的函数。来一小段 Python 代码绘制一下这个函数,
# compare probability vs information entropy
from math import log2
from matplotlib import pyplot
# list of probabilities
probs = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
# calculate information
info = [-log2(p) for p in probs]
# plot probability vs information
pyplot.plot(probs, info, marker='.')
pyplot.title('Probability vs Information')
pyplot.xlabel('Probability')
pyplot.ylabel('Information')
pyplot.show()
结果见下图,对照一下图像来更好地理解一下这个函数吧。
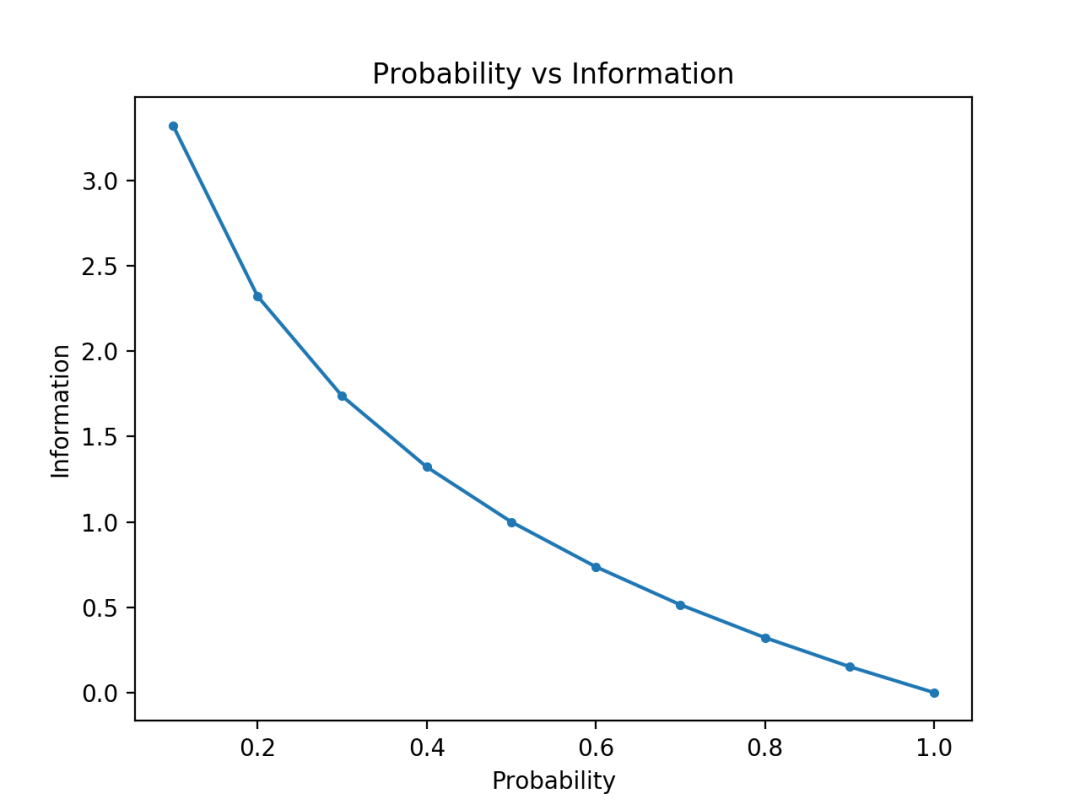
好了,接下来我们就用这个函数来计算信息熵。熵,从数学上看,衡量的是一种期望值,即随机变量多次试验后所传递的信息量的平均值。假设离散随机变量对应的分布为
这里用的都是以 2 为底的对数,也因此信息量对应的单位称为比特(bit)。下面我们回到前文的例子。
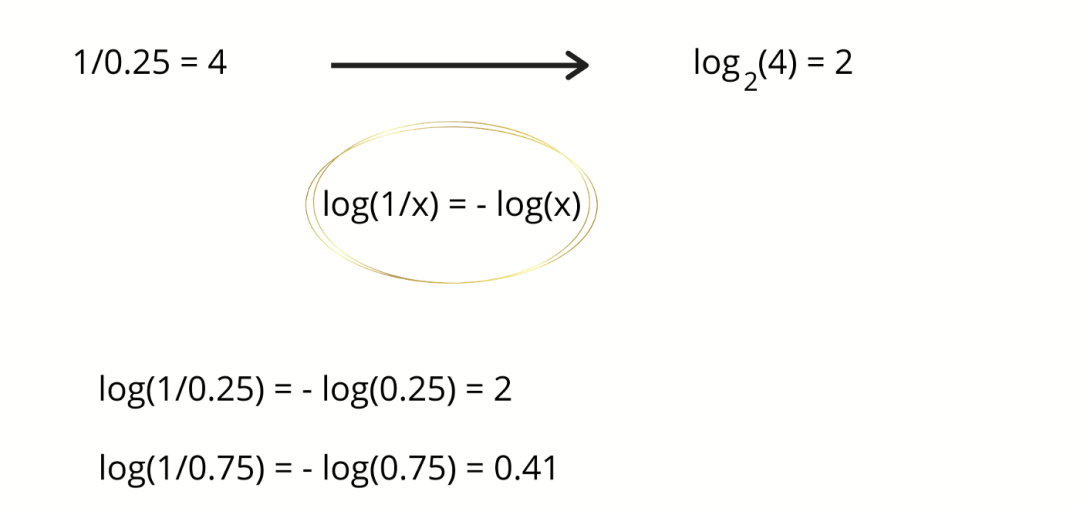
如果气象站说第二天是晴天,那么我们将获得 0.41 比特的信息量。因此,平均而言,我们将从气象站获得多少信息量呢?
好吧,明天有 75% 的机率是晴天,这会给你 0.41 比特的信息,明天有 25% 的机率会下雨,它为给你提供 2 比特的信息,对应于下图
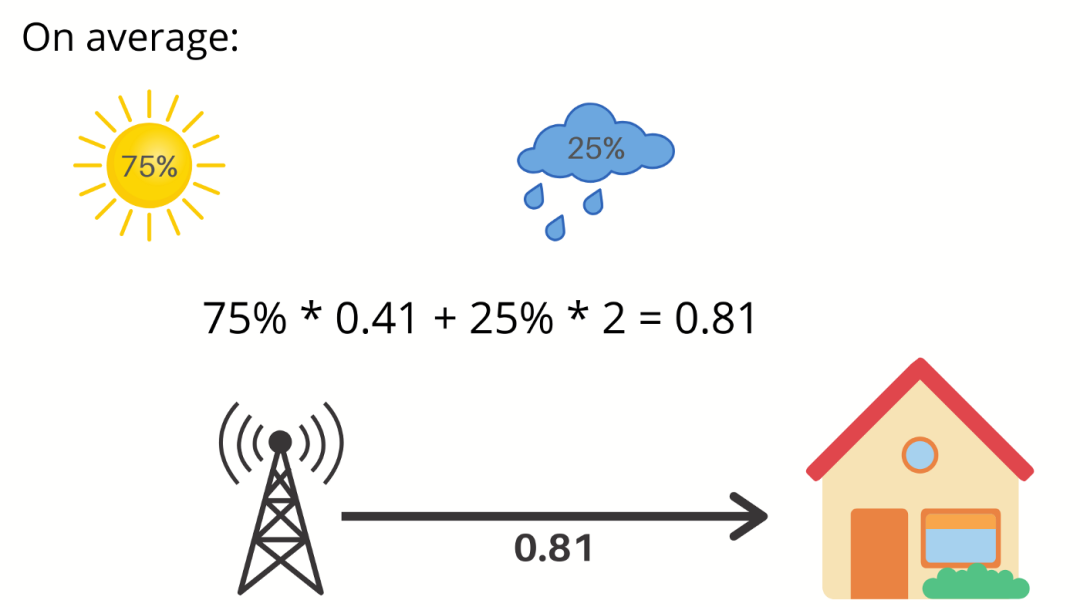
平均而言,我们每天从气象站获得 0.81 比特的信息。因此,我们把刚刚计算出的平均值称为信息熵。这很好地衡量了事件的不确定性。
希望熵的公式现在完全有了意义。它衡量的是你每天收到天气预报时得到的平均信息量。通常,它给出了我们从给定的概率分布
如果我们生活在每天阳光明媚的沙漠中,平均来说,每天我们不会从气象站获得太多信息。熵值将接近于零。另一方面,如果每天的天气情况变化很大,熵值将很大。
3交叉熵
现在,让我们谈谈交叉熵。可以将它看成平均信息长度。比如上面例子中,考虑到有 8 种可能的天气状况,它们的可能性均等,可以使用 3 个比特的信息对每种状况来编码。
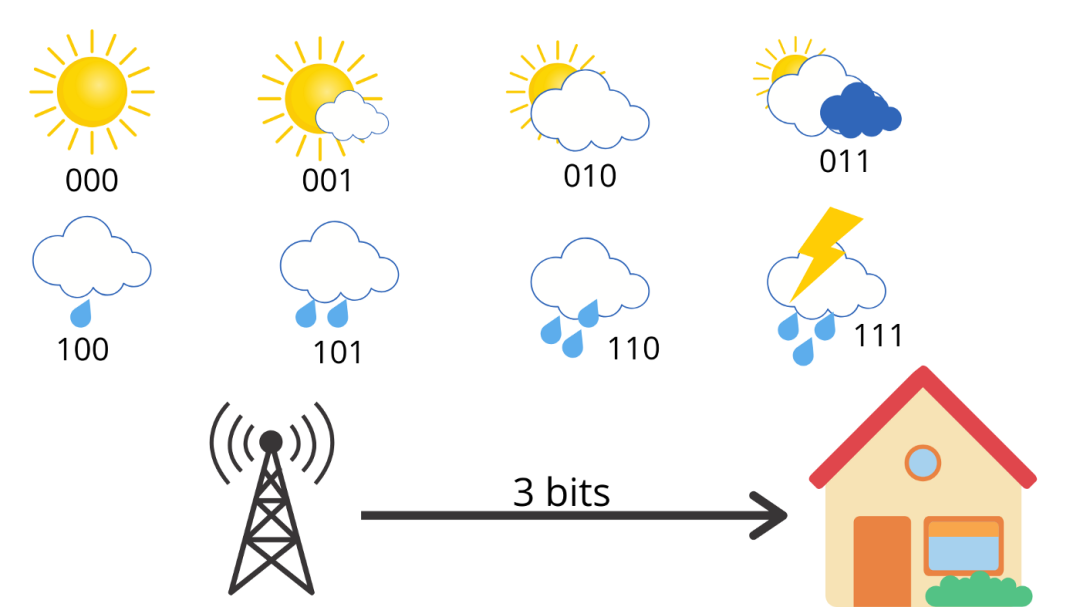
如图所示,这里的平均信息长度为 3,这就是这个例子的交叉熵。
但是现在,假设你住在阳光充足的地区,天气的概率分布并不均匀,具体如下图所示,
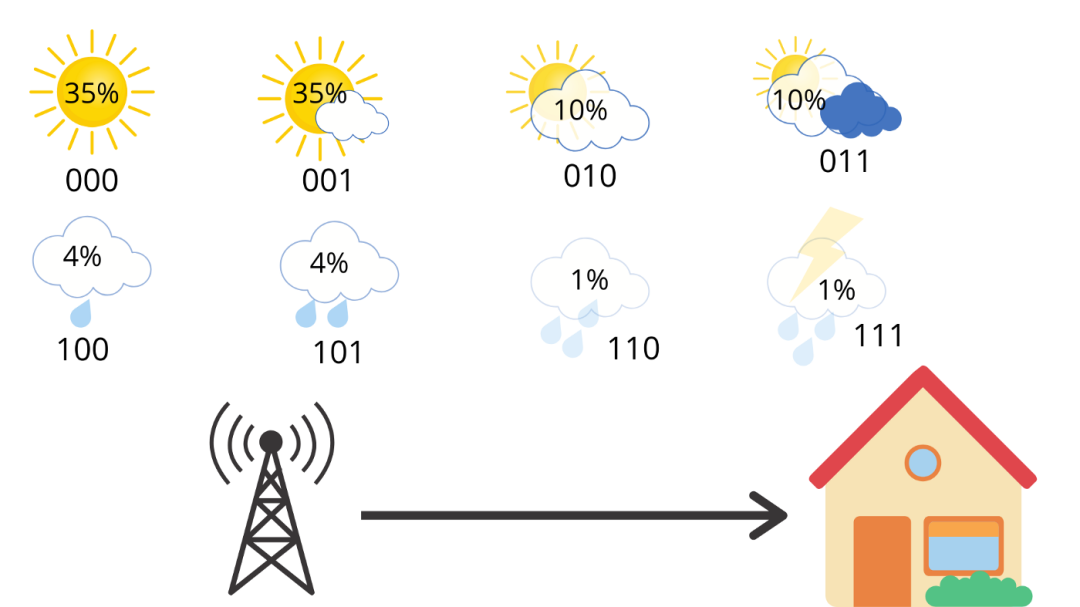
每天都有 35% 的机率是晴天,雷雨的可能性只有 1%。因此,我们可以计算该概率分布的熵,得,
请注意,此处使用的是以 2 为底的对数。
因此,气象站平均发送 3 个比特信息,但是接收者仅获得 2.23 个有用的比特信息。那么,是不是说明我们还可以做得更好呢?
例如,像下面这样来更改编码,
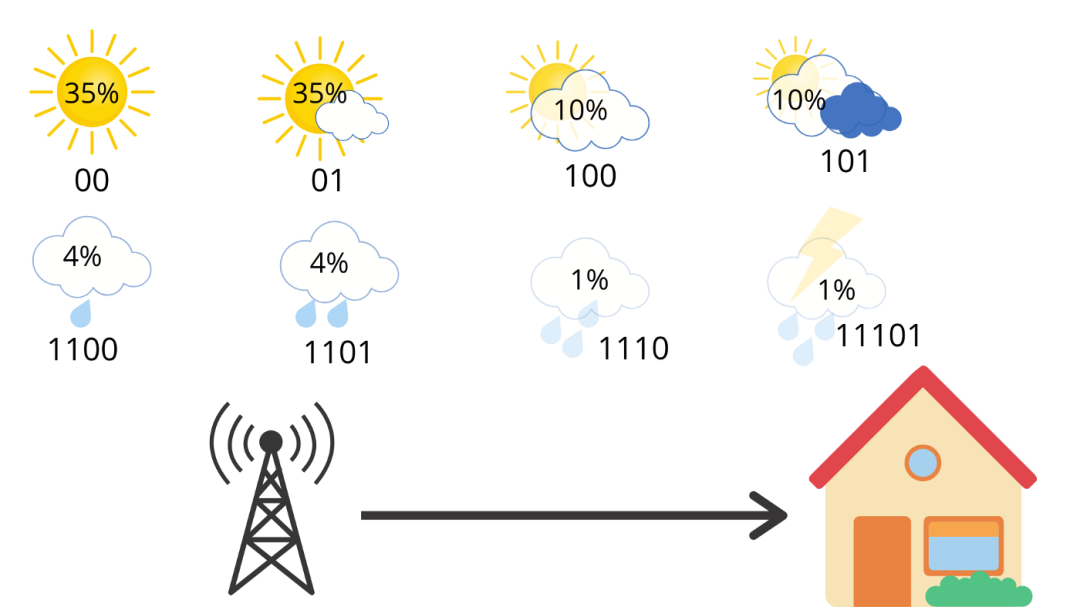
现在,我们只使用 2 个比特信息表示晴天或部分晴天,使用 3 个比特信息表示多云和大部分多云,使用 4 个比特信息表示中雨和小雨,使用 5 个比特信息表示大雨和雷暴。对天气坐这样的编码方式是不会引起歧义的,例如,你链接多条消息,则只有一种方法可以解释比特流。例如,01100 只能表示部分晴天(01),然后是小雨(100)。因此,如果我们计算该站每天发送的平均比特数,则可以得出,
这是我们新的和改进的交叉熵,它比以前的 3 个比特更好。现在,假设我们在不同的地方使用相同的代码,那儿的天气是相反的,多雨。
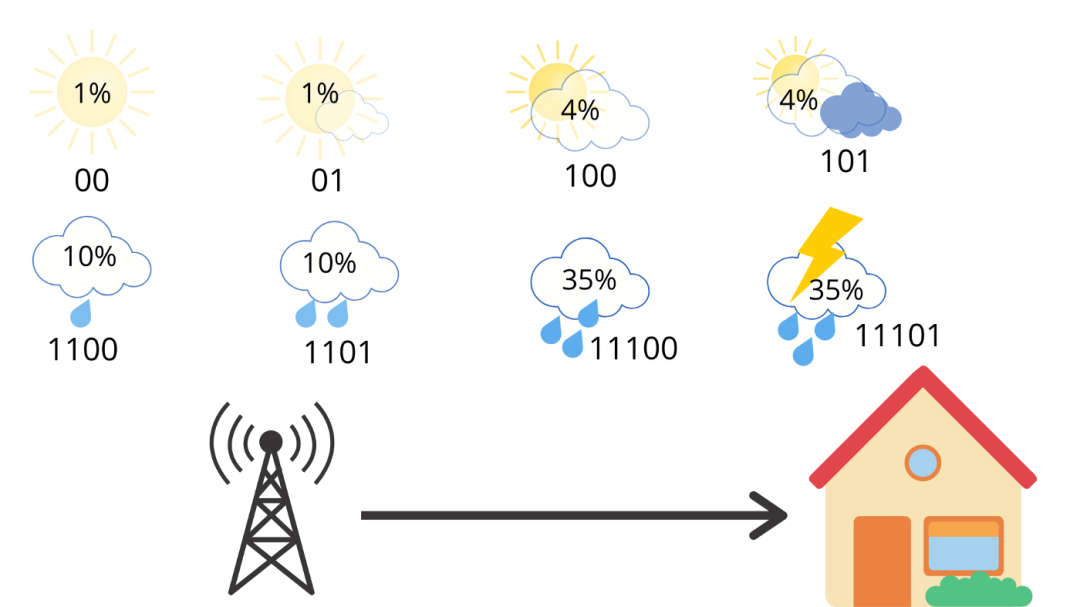
现在,如果我们计算交叉熵,
我们得到 4.58 个比特,大约是熵的两倍。平均而言,该站发送 4.58 个比特信息,但只有 2.23 个比特信息对接收者来说是有用的。每条消息发送的信息量是必要信息的两倍。这是因为我们使用的代码对天气分布做出了一些隐含的假设。例如,当我们在晴天使用 2 个比特信息时,我们含蓄地预测了晴天的概况为 25%。这是因为
同样,我们计算所有的天气情况。
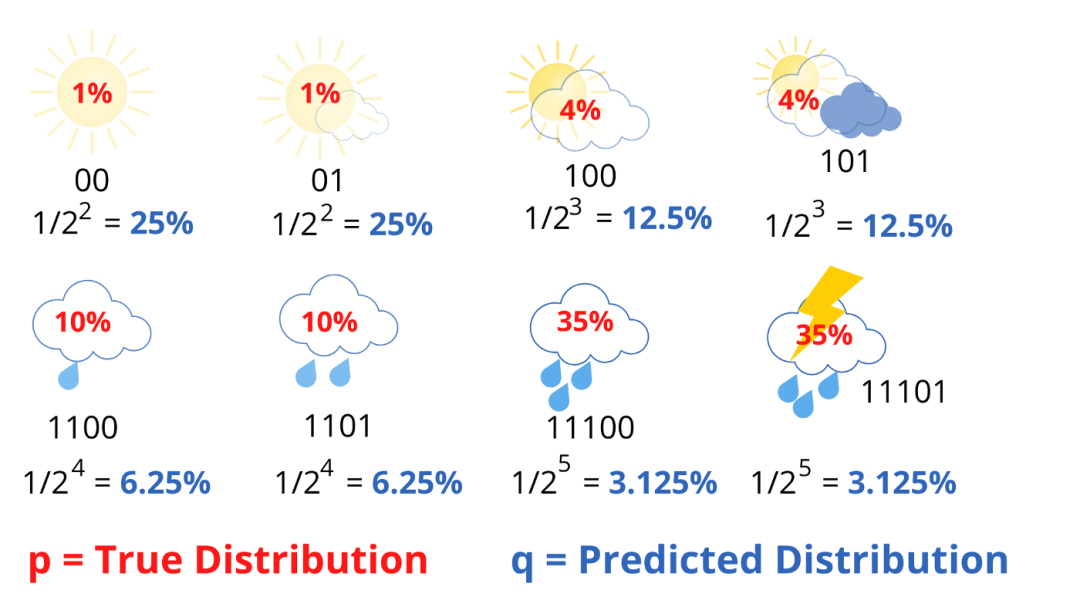
分母中 2 的幂对应于用于传输信息的比特数。很明显,预测分布
因此,现在我们可以将交叉熵(
请注意,本示例中使用的对数均是以 2 为底的。
正如你所见,除了我们在这里使用预测概率的对数外,它看起来与熵的等式非常相似。如果我们的预测是完美的,那就是预测分布等于真实分布,那么交叉熵就等于熵。但是,如果分布不同,交叉熵就会比熵更大一些,因为多了一些比特。交叉熵超过熵的数量,被称为相对熵,或更通常称为 Kullback-Leibler Divergence(KL-散度)。总结一下,简而言之,
从上面的例子中,我们得到
4应用
现在,让我们在实际应用中来用一用交叉熵。比如,我们正在训练一个图像分类器,对看起来比较相似的不同动物进行分类,例如浣熊啊、小熊猫啊、狐狸之类等等。
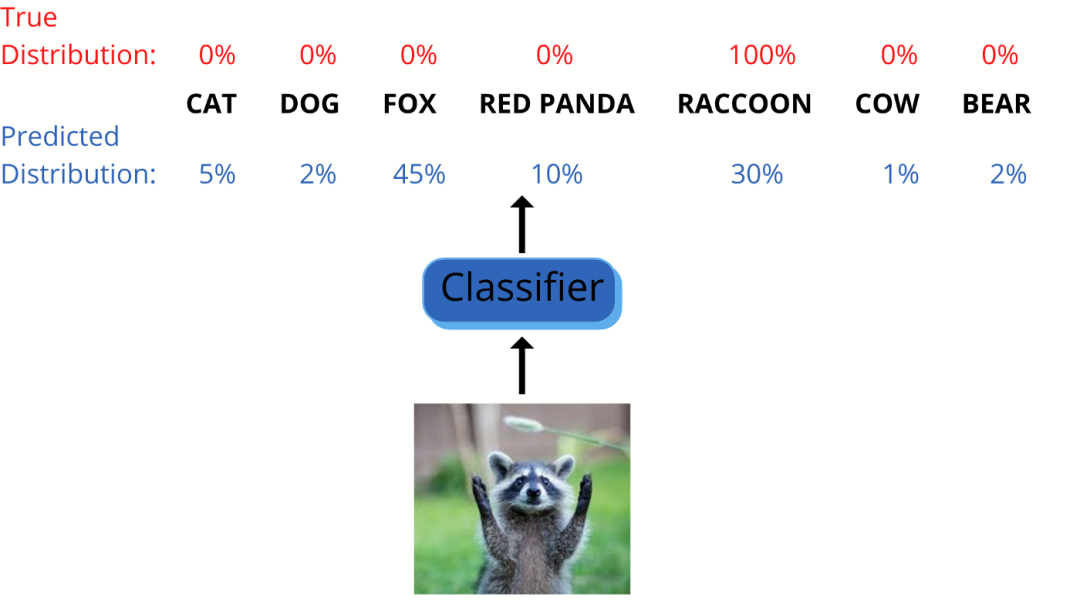
因此,对于可能的 7 个类别中的每一个类别,分类器会分别给出一个概率,即所谓的预测分布。由于这是有监督的学习问题,因此我们是知道真实分布的。
在上面的示例中,我拍了一只浣熊的照片,因此在真实分布中,浣熊类的概率应该为 100%,其他类的概率为 0。我们可以将这两个分布之间的交叉熵作为成本函数,称为交叉熵损失。
这只是我们前面看到的等式,除了它通常使用自然对数而不是 以 2 为底的对数。对于训练而言,这无关紧要,因为以 2 为底的对数
因此,当类别概率被称为一个独热编码向量(这意味着一个类别具有 100% 概率,其余类别均为 0%)时,交叉熵只是真实类别的估计概率的负对数。
在这个例子中,交叉熵为
现在,你可以看到,当对真实类别的预测概率接近 0 时,成本函数可能会非常大。但是,当预测概率接近 1 时,成本函数将接近 0。因此,我们需要对每个类使用更多的例子来训练分类器,以减少损失。
5小结
我们以气象站更新第二天的天气为例,了解了香农信息理论的概念。然后我们将其与熵、交叉熵相关联。最后,我们使用一个例子看了下交叉熵损失函数的实际用法。我希望本文能帮大家弄清熵、交叉熵和 KL-散度以及他们之间的联系。
⟳参考资料⟲
Hands-On Machine Learning with Scikit-Learn and TensorFlow: https://www.oreilly.com/library/view/hands-on-machine-learning/9781491962282/
[2]Entropy, Cross-Entropy, and KL-Divergence Explained: https://towardsdatascience.com/entropy-cross-entropy-and-kl-divergence-explained-b09cdae917a
[3]A Gentle Introduction to Information Entropy: https://machinelearningmastery.com/what-is-information-entropy
[4]Entropy_information_theory: https://en.wikipedia.org/wiki/Entropy_information_theory
↓扫描二维码添加好友↓ 推荐阅读
(点击标题可跳转阅读)
