可以借助归并排序秒杀的面试题!
共 1724字,需浏览 4分钟
·
2021-02-16 22:59
哎嘛,这假期过的可真快啊,又要早起搬砖了,那咱们就接着来做题吧,牛年一起冲冲冲!咱们今天继续说归并排序。
归并排序是面试的高频考点,下面我们来一起看看如何借助归并排序解决逆序对,翻转对问题。在 leetcode 上面属于困难题目。
大家做题之前可以顺便解决一下这个题目,leetcode 912 排序数组,这个题目大家可以用来练手,因为有些排序算法是面试高频考点,所以大家可以多用这个题目进行练习,防止手生。
下面则是我写文章时代码的提交情况,冒泡排序怎么优化都会超时,其他排序算法倒是都可以通过。
下面我们一起来看一下,如何利用归并排序来解决逆序对问题,其实很简单,我们仅仅需要在之前的归并排序添加一行代码即可,我们首先来看一下什么是逆序对。继续用之前的例子。
逆序对:在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对,见下图。
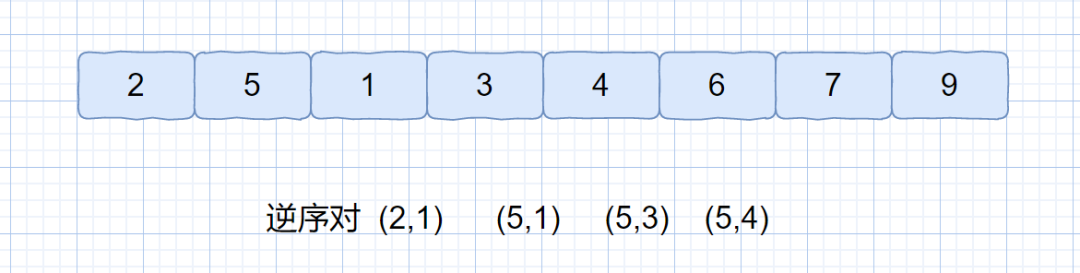
是不是很容易理解,因为数组是无序的,当较大的数,出现在较小数前面的时候,它俩则可以组成逆序对。
数组的(有序度+逆序度)= n (n-1) / 2,n代表元素个数,逆序对个数 = 数组的逆序度,有序对个数 = 数组的有序度,所以我们知道有序对个数的话,自然能得到逆序对的个数。
那么我们如何通过归并排序来计算逆序对个数呢?
关键点在我们的归并过程中,我们先来看下归并过程中是怎么计算逆序对个数的。见下图
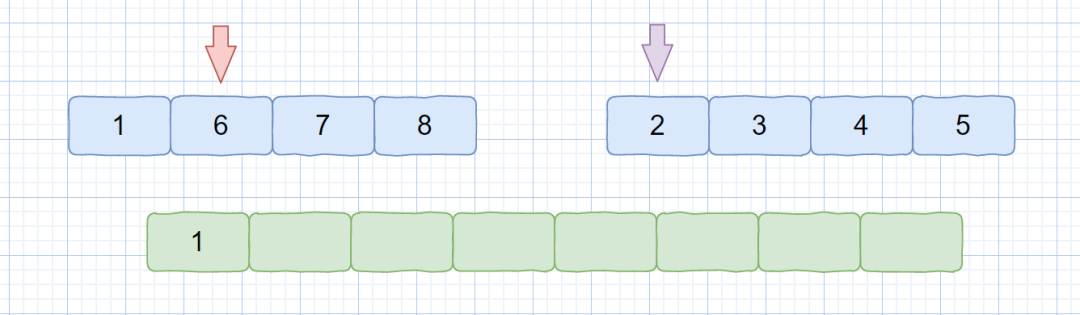
我们来拆解下上图,我们此时 temp1 指向元素为 6,temp2 指向元素为 2, nums[temp1] > temp[temp2]。
则此时我们需要将 temp2 指向的元素存入临时数组中,又因为每个小集合中的元素都是有序的,所以 temp1 后面的元素也一定大于 2。那么我们就可以根据 temp1 的索引得出当前情况下的逆序对个数,则是 mid - temp1 + 1。
好啦这个题目你已经会做啦,下面我们一起来做下吧。
剑指 Offer 51. 数组中的逆序对
题目描述
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
示例 1:
输入: [7,5,6,4]
输出: 5
题目解析
各位如果忘记归并排序的话,可以再看一下咱们之前的文章回顾一下 归并排序详解,这个题目我们仅仅在归并排序的基础上加了一行代码。那就是在归并过程时,nums[temp2] < nums[temp1] 时统计个数。下面我们直接看代码吧。
题目代码
class Solution {
//全局变量
private int count;
public int reversePairs(int[] nums) {
count = 0;
merge(nums,0,nums.length-1);
return count;
}
public void merge (int[] nums, int left, int right) {
if (left < right) {
int mid = left + ((right - left) >> 1);
merge(nums,left,mid);
merge(nums,mid+1,right);
mergeSort(nums,left,mid,right);
}
}
public void mergeSort(int[] nums, int left, int mid, int right) {
int[] temparr = new int[right-left+1];
int index = 0;
int temp1 = left, temp2 = mid+1;
while (temp1 <= mid && temp2 <= right) {
if (nums[temp1] <= nums[temp2]) {
temparr[index++] = nums[temp1++];
} else {
//增加的一行代码,用来统计逆序对个数
count += (mid - temp1 + 1);
temparr[index++] = nums[temp2++];
}
}
if (temp1 <= mid) System.arraycopy(nums,temp1,temparr,index,mid-temp1+1);
if (temp2 <= right) System.arraycopy(nums,temp2,temparr,index,right-temp2+1);
System.arraycopy(temparr,0,nums,left,right-left+1);
}
}
好啦,这个题目我们就解决啦,哦对,大家也可以顺手去解决下这个题目。
下面我们继续解决翻转对问题,也完全可以用归并排序解决,稍微加了一丢丢代码,也是很好理解的。
leetcode 493. 翻转对
题目描述
给定一个数组 nums ,如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。
你需要返回给定数组中的重要翻转对的数量。
示例 1:
输入: [1,3,2,3,1]
输出: 2
示例 2:
输入: [2,4,3,5,1]
输出: 3
题目解析
我们理解了逆序对的含义之后,题目理解起来完全没有压力的,这个题目第一想法可能就是用暴力法解决,但是会超时,所以我们有没有办法利用归并排序来完成呢?
我们继续回顾一下归并排序的归并过程,两个小集合是有序的,然后我们需要将小集合归并到大集合中,则我们完全可以在归并之前,先统计一下翻转对的个数,然后再进行归并,则最后排序完成之后自然也就得出了翻转对的个数。具体过程见下图。

此时我们发现 6 > 2 * 2,所以此时是符合情况的,因为小数组是单调递增的,所以 6 后面的元素都符合条件,所以我们 count += mid - temp1 + 1;则我们需要移动紫色指针,判断 2 的后面是否还存在符合条件的情况。

我们此时发现 6 = 3 * 2,不符合情况,因为小数组都是完全有序的,所以后面没有符合条件的情况了,则我们可以移动红色指针,看 6 后面的数有没有符合条件的情况,重复上诉过程,直至遍历结束。
这样我们就可以得到翻转对的数目啦。
大家思考一下为什么我们不可以和逆序对一样在归并到大集合时统计?
可以看一下这个样例两个小集合分别是[-5,-2,1],[-4,-3,5],如果不进行遍历统计,只在合并时统计,则会漏掉某些情况。
下面我们直接看视频加深下印象吧!
是不是很容易理解啊,那我们直接看代码吧,仅仅是在归并排序的基础上加了几行代码用于统计翻转对。
题目代码
class Solution {
private int count;
public int reversePairs(int[] nums) {
count = 0;
merge(nums, 0, nums.length - 1);
return count;
}
public void merge(int[] nums, int left, int right) {
if (left < right) {
int mid = left + ((right - left) >> 1);
merge(nums, left, mid);
merge(nums, mid + 1, right);
mergeSort(nums, left, mid, right);
}
}
public void mergeSort(int[] nums, int left, int mid, int right) {
int[] temparr = new int[right - left + 1];
int temp1 = left, temp2 = mid + 1, index = 0;
//计算翻转对
while (temp1 <= mid && temp2 <= right) {
//这里需要防止溢出
if (nums[temp1] > 2 * (long) nums[temp2]) {
count += mid - temp1 + 1;
temp2++;
} else {
temp1++;
}
}
//记得归位,我们还要继续使用
temp1 = left;
temp2 = mid + 1;
//归并排序
while (temp1 <= mid && temp2 <= right) {
if (nums[temp1] <= nums[temp2]) {
temparr[index++] = nums[temp1++];
} else {
temparr[index++] = nums[temp2++];
}
}
//照旧
if (temp1 <= mid) System.arraycopy(nums, temp1, temparr, index, mid - temp1 + 1);
if (temp2 <= right) System.arraycopy(nums, temp2, temparr, index, right - temp2 + 1);
System.arraycopy(temparr, 0, nums, left, right - left + 1);
}
}
好啦,我们的文章到这就结束啦,希望对你有一丢丢帮助啊。是不是觉得这两个困难题很简单啊,大家可以去写一下啦。
