全新激活函数 | 详细解读:HP-x激活函数(附论文下载)


1简介
本文提出了orthogonal-Padé激活函数,它是可以训练的激活函数,在标准深度学习数据集和模型中具有更快的学习能力,同时可以提高模型的准确率。根据实验,在六种orthogonal-Padé激活中找到了2种最佳的候选函数,作者称之为 safe Hermite-Pade(HP)激活函数,即HP-1和HP-2。
与ReLU相比,HP-1和HP-2帮助PreActResNet-34带来不同程度的提升(top-1精度提升分别为5.06%和4.63%),在CIFAR100数据集上MobileNet V2模型提升分别为3.02%和2.75%分别,在CIFAR10数据集上PreActResNet-34的top-1精度分别增加了2.02%和1.78%,LeNet的top-1精度分别提升为2.24%和2.06%,Efficientnet B0的top-1精度分别提升为2.15%和2.03%。
2前人工作简介
深度卷积神经网络由多个隐藏层和神经元构成。然后通过每个神经元的激活函数引入非线性。
ReLU由于其简单性,是深度学习中最受欢迎的激活函数。虽然ReLU有一个缺点叫做 dying ReLU,在这种情况下,多达50%的神经元可能会因为消失梯度问题,即有大量的神经元对网络性能没有影响。为了克服这一问题,后来又提出了Leaky Relu、Parametric Relu、ELU、Softplus,虽然找到最佳的激活函数仍是一个有待研究的问题,但这些方法都提高了网络的性能。最近,研究人员使用了自动搜索技术发现了Swish激活函数。与ReLU相比,Swish的精确度有了一些提高。GELU、Mish、TanhSoft、EIS是目前少数几个可以替代ReLU和Swish的候选激活函数。
近年来,人们对可训练激活函数的研究也越来越感兴趣。可训练激活函数具有可学习的超参数(s),在训练过程中通过反向传播算法更新。本文提出了Orthogonal-Padé激活函数。Orthogonal-Padé函数可以近似大多数连续函数。
3Padé activation Unit (PAU) and Orthogonal-PAU
考虑实线的一个闭合间隔为[a,b]。设 是 中次数小于等于 的所有多项式的空间。对于一个非负连续函数 ,在[a, b]上定义Pn(x)上的内积为:
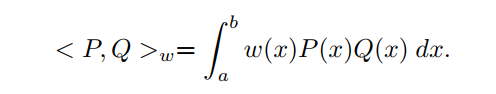
有多项式是正交的,如果:
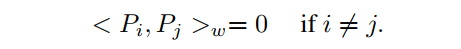
的一组基是由 张成的n个多项式的集合。一组正交基也是一组正交集。
的标准基是 。但是标准基与式1中定义的内积并不是正交的。
在许多应用中,使用正交基可以简化表达式并减少计算。多项式空间有几个众所周知的正交基。下表列出了其中一些多项式基。注意,它们有的由递归关系给出,有的由直接表达式给出。

3.1 Padé activation Unit (PAU)
f(x)由有理函数F1(x)的Padé近似定义为:
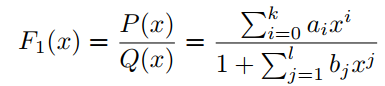
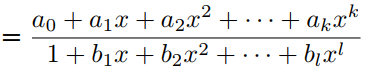
其中P(x)和Q(x)分别是k次和l次的多项式,它们没有公因式。PAU是式(3)的可学习激活函数,其中多项式系数 为可学习参数,在反向传播过程中进行更新。为了将F1(x)的极点从Q(x)的0中移除,有学者提出了safe PAU。safe PAU定义为:
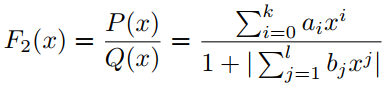
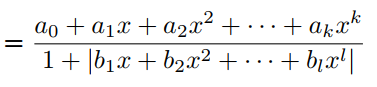
在分母中引入绝对值可以确保分母不会消失。实际上,也可以取和的绝对值来定义:
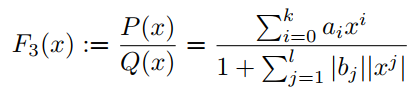
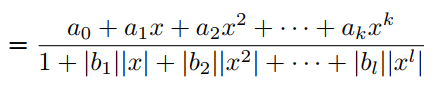
在许多任务中,F3定义的激活函数比F2定义的safe PAU能够提供更好的结果。
3.2 Orthogonal-Padé activation Unit (OPAU)
g(x)由有理函数G(x)的orthogonal-Padé近似定义为:
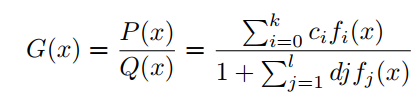
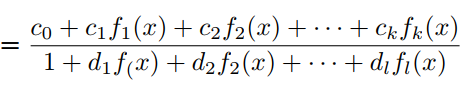
其中 属于正交多项式集合。与PAU一样,可学习激活函数OPAU由(6)定义,其中 为可学习参数。参数的初始化是通过近似的形式的如ReLU, Leaky ReLU等。为了去掉G(x)的极点,提出如下的safe OPAU。
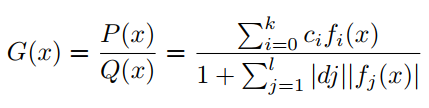
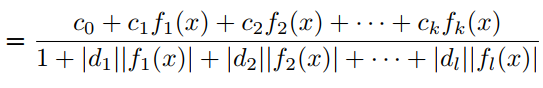
作者考虑了6种正交多项式基- Chebyshev(两种),Hermite(两种),Laguerre和Legendre多项式的基。关于这些多项式基的详细信息见表1。
3.3 通过反向传播学习激活参数
利用反向传播算法和梯度更新神经网络模型中的权值和偏差。这里也采用相同的方法更新激活函数的参数。作者已经在Pytorch和Tensorflow-Keras API实现了自动化更新参数。对输入x和参数 计算公式(6)的梯度如下:
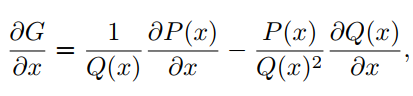
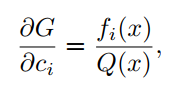
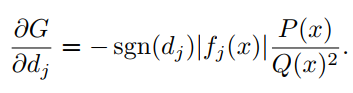
4具有orthogonal-Padé激活以及函数近似的网络
Orthogonal-Padé网络类似于Padé网络,即将具有PAU或safe PAU的网络替换为OPAU或safe OPAU。在本文中,将safe OPAUs视为不同正交基的激活函数,如表1所示。用(7)中给出的函数形式近似Leaky ReLU对可学习参数(多项式系数)进行初始化,初始化参数值如下表所示。
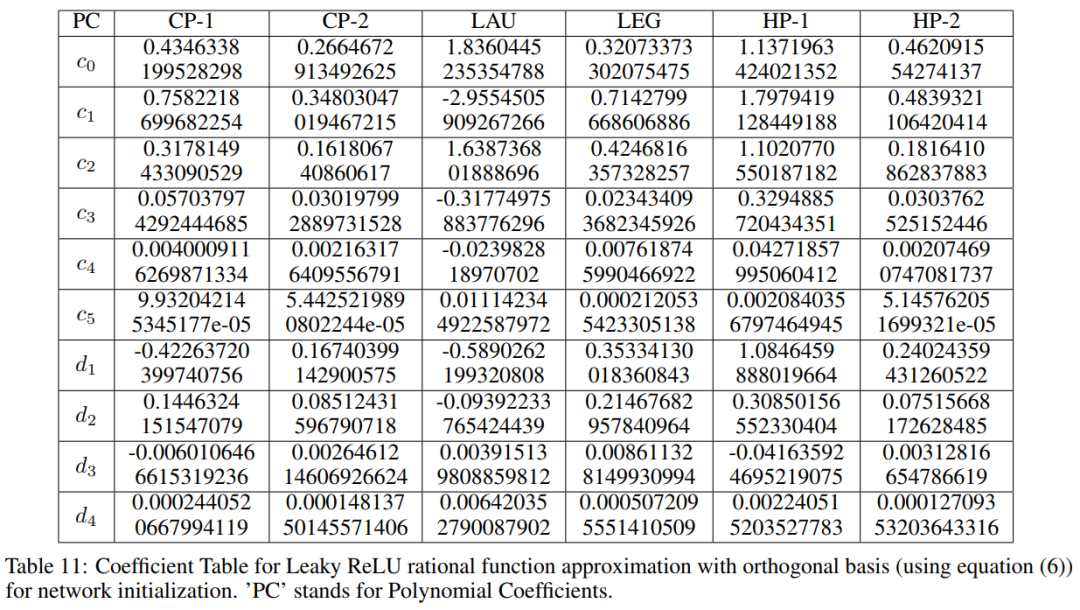
利用反向传播方法对网络参数进行了优化。作者对所有的网络都保持了PAU的类似设计,例如每层的权重共享和可学习激活参数。由式(5)可知,每层总共有(k+l)个额外参数。因此,如果网络中有L层,网络中就会有额外的L(k+L)个可学习参数。为了训练网络,作者采用了Leaky ReLU初始化(α=0.01),而不是随机初始化方法。
使用正交基的一个主要优点是,与标准基相比,可以在运行时间上更快地找到多项式系数。此外,目前广泛使用的激活函数在大多数情况下是零中心的。因此作者在Padé和Orthogonal-Padé近似上施加一些条件,以使已知函数近似为零中心,并检查是否有任何对模型性能的优势(一个明显的优势是每一层的参数量减少了)。
为了使Padé以零为中心,将式(4)中的 替换,并计算其他参数。为了保证OPAU的safe,会有几个bad case,作者研究了所有可能的bad case。
例如,如果选择HP-1作为基,如果分子中的常数项为零,则安全的OPAU函数近似可以以零为中心。由式(6)和表1可知, 。可以推导出以下情况:
case 1:
case 2:
其中一个等于0。例如,如果 ,那么 等等;
case 3:
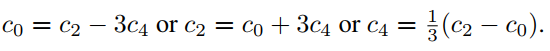
在上述PAU和HP-1的所有情况下,作者已经在CIFAR10和CIFAR100数据集上对几个经典的模型进行了实验和测试(Leaky ReLU近似)。作者发现在大多数情况下,模型在top-1准确率下降了0.2%-0.6%。
此外,需要注意的是,具有safe OPAU激活函数的神经网络在C(K)中是dense的,其中K是 的一个紧凑子集,而C(K)是K上所有连续函数的空间。
Proposition
-
设 是任意连续函数。设 表示一类具有激活函数 的神经网络,输入层有n个神经元,输出层有1个神经元,隐层有任意数量的神经元。设 是compact的。当且仅当 是非多项式时, 在C(K)中是dense的。
-
设 是任意连续函数,它至少在一点上是连续可微的,且在这一点上导数为非零。设 是compact的。那么在 中, 是dense的。
5实验
5.1 CIFAR-100
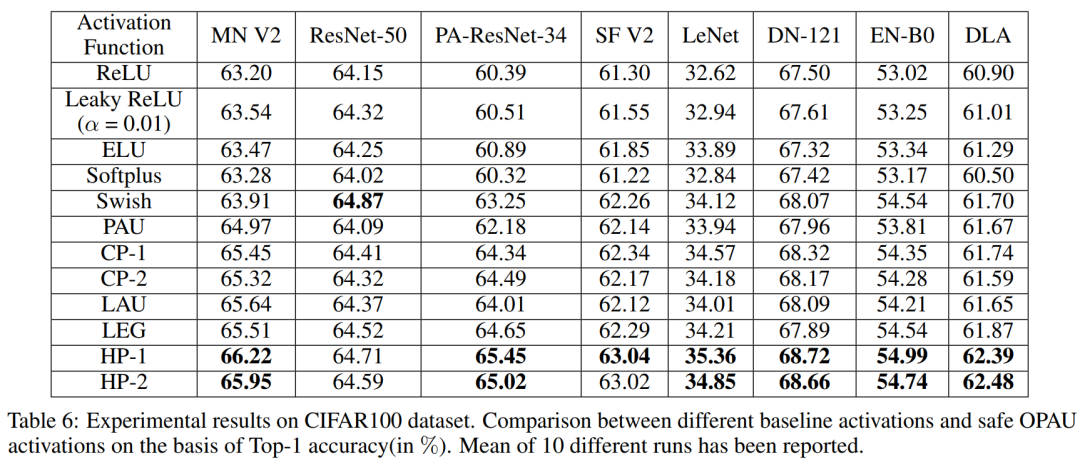
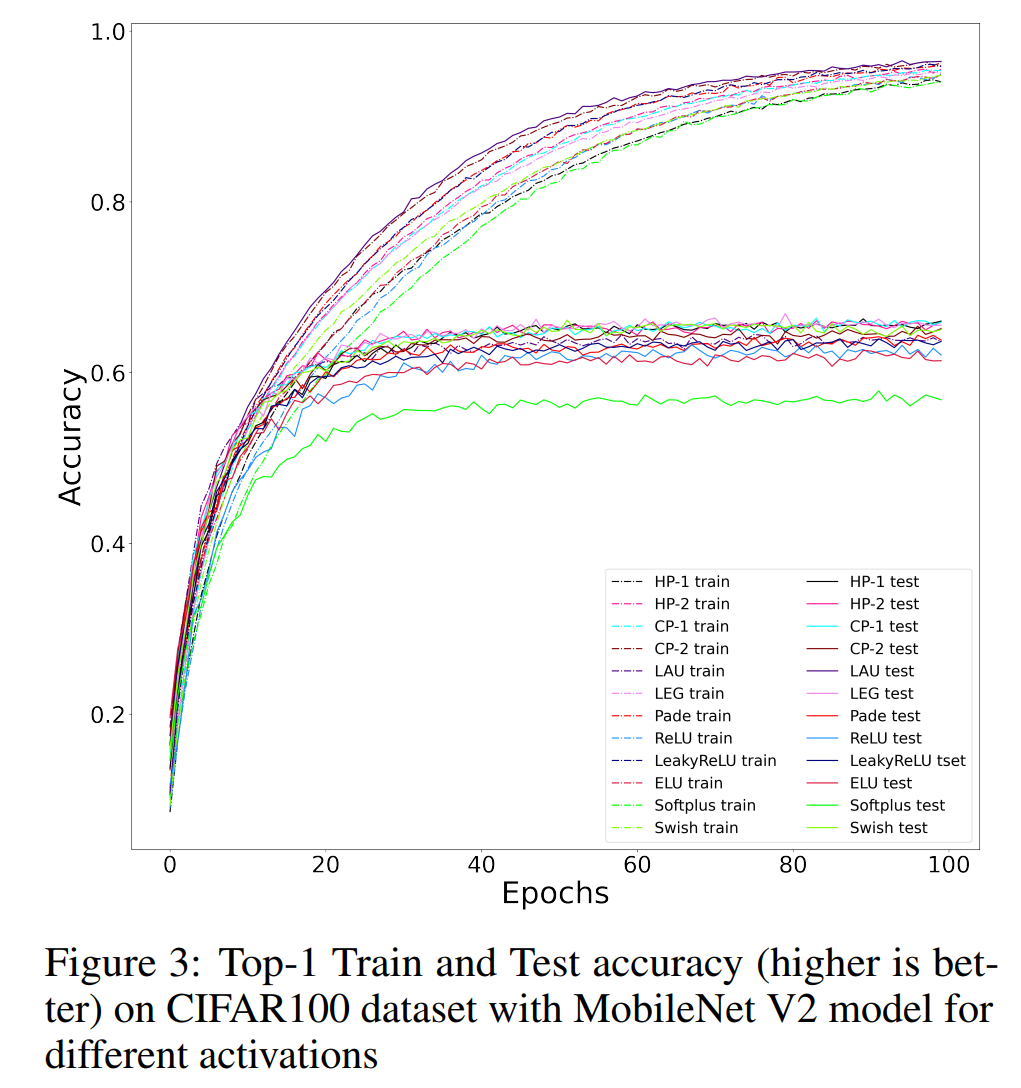
5.2 Tiny Imagenet
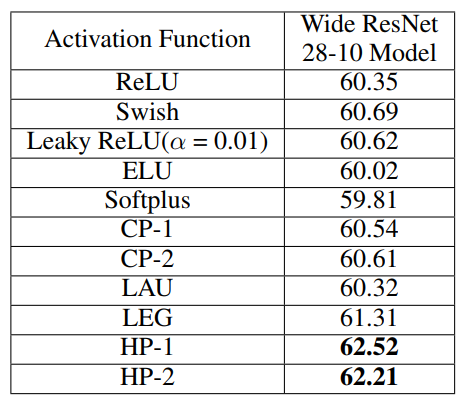
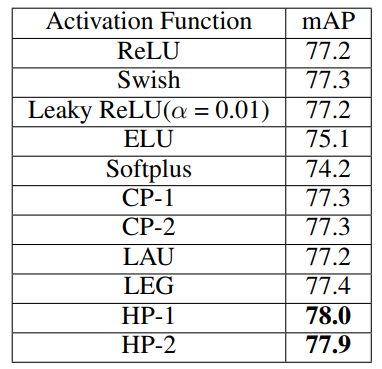
5.3 VOC 2007
6参考
[1].ORTHOGONAL-PADÉ ACTIVATION FUNCTIONS: TRAINABLE ACTIVATION FUNCTIONS FOR SMOOTH AND FASTER CONVERGENCE IN DEEP NETWORKS
7推荐阅读

遮挡人脸问题 | 详细解读Attention-Based方法解决遮挡人脸识别问题(附论文下载)

效率新秀 | 详细解读:如何让EfficientNet更加高效、速度更快

Transformer | 详细解读Transformer怎样从零训练并超越ResNet?
本文论文原文获取方式,扫描下方二维码
回复【HPX】即可获取论文
长按扫描下方二维码添加小助手。
可以一起讨论遇到的问题
声明:转载请说明出处
扫描下方二维码关注【集智书童】公众号,获取更多实践项目源码和论文解读,非常期待你我的相遇,让我们以梦为马,砥砺前行!

