看了这篇,HashMap底层原理终于搞懂了!
点击上方蓝色字体,选择“标星公众号”
优质文章,第一时间送达
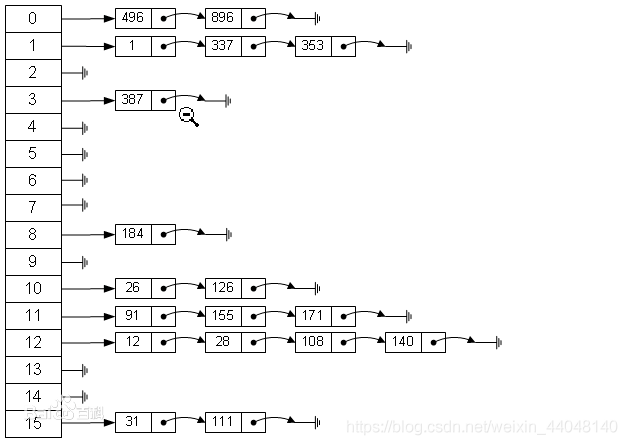
HashMap结构图
代码分析
常见的参数及意义
//默认的Hash表的长度
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
//Hash表的最大长度
static final int MAXIMUM_CAPACITY = 1 << 30;
//默认加载因子
static final float DEFAULT_LOAD_FACTOR = 0.75f;
//当链表的长度为8的时候转化为红黑树
static final int TREEIFY_THRESHOLD = 8;
//桶中元素个数小于6的时候红黑树转换为链表
static final int UNTREEIFY_THRESHOLD = 6;
//只有当数组的长度大于等于64并且链表个数大于8才会转换为红黑树
static final int MIN_TREEIFY_CAPACITY = 64;
//Hash表
transient Node<K,V>[] table;
//遍历的时候使用返回一个K-V集合
transient Set<Map.Entry<K,V>> entrySet;
//表中K-V的个数
transient int size;
//对集合的修改次数,主要是后面出现的集合校验
transient int modCount;
//阈值当size大于threshold时就会进行resize
int threshold;
//加载因子
final float loadFactor;
源码解释
构造方法
//传入初始化容量,和指定的加载因子
public HashMap(int initialCapacity, float loadFactor) {
//参数校验
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
//如果传入的值大于最大容量,就将最大的值赋给他
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
//参数校验
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
//返回的是2的整数次幂
this.threshold = tableSizeFor(initialCapacity);
}
//指定HashMap的容量
public HashMap(int initialCapacity) {
//调用如上的双参构造函数
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
//无参构造函数
public HashMap() {
//初始化加载因子为默认的加载因子
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}
//构造一个映射关系与指定 Map 相同的新 HashMap。
public HashMap(Map<? extends K, ? extends V> m) {
//初始化加载因子为默认的加载因子
this.loadFactor = DEFAULT_LOAD_FACTOR;
//构造的过程函数
putMapEntries(m, false);
}
final void putMapEntries(Map<? extends K, ? extends V> m, boolean evict) {
//获取m集合中元素个数
int s = m.size();
//如果m集合元素个数是0个那么下面这些操作也就没有必要了
if (s > 0) {
if (table == null) { //表示的拷贝构造函数调用putMapEntries函数,或者是构造了HashMap但是还没有存放元素
//计算的值存在小数所以+1.0F向上取整
float ft = ((float)s / loadFactor) + 1.0F;
//将ft强制转换为整形
int t = ((ft < (float)MAXIMUM_CAPACITY) ?
(int)ft : MAXIMUM_CAPACITY);
//如果计算出来的值大于当前HashMap的阈值更新新的阈值为2次方
if (t > threshold)
threshold = tableSizeFor(t);
}
else if (s > threshold)//如果Map集合元素大于当前集合HashMap的阈值则进行扩容
resize();
//将Map集合中元素存放到当前集合中
for (Map.Entry<? extends K, ? extends V> e : m.entrySet()) {
K key = e.getKey();
V value = e.getValue();
putVal(hash(key), key, value, false, evict);
}
}
}
size函数
//返回key-val的数量
public int size() {
return size;
}
isEmpty函数
//当前的集合是否为null
public boolean isEmpty() {
return size == 0;
}
get具体过程函数
//根据key获取对应的val
public V get(Object key) {
Node<K,V> e;
//通过hash值,key找到目标节点再返回对应的val
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
//获取key对应的节点
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
//如果集合为空和对应的下标数组中的值为空直接返回null
//first = tab[(n - 1) & hash]数组的长度是2n次方减1后对应位全部变为1,这样为与操作永远都会在数组下标范围内不会越界
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
if (first.hash == hash && // 如果第一个节点hash与对应hash相等,并且key也相等则返回当前节点
((k = first.key) == key || (key != null && key.equals(k))))
return first;
//第一个节点的下一个节点不为null
if ((e = first.next) != null) {
//判断节点是否为树形
if (first instanceof TreeNode)
//在树形结构中查找节点并返回
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
do {//通过do...while结构遍历找对应key的节点
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
//找到节点并返回
return e;
} while ((e = e.next) != null);
}
}
//未找到对应的节点
return null;
}
containsKey函数
//查看是否包含指定key
public boolean containsKey(Object key) {
//通过getNode返回是否为null判断是否存在key
return getNode(hash(key), key) != null;
}
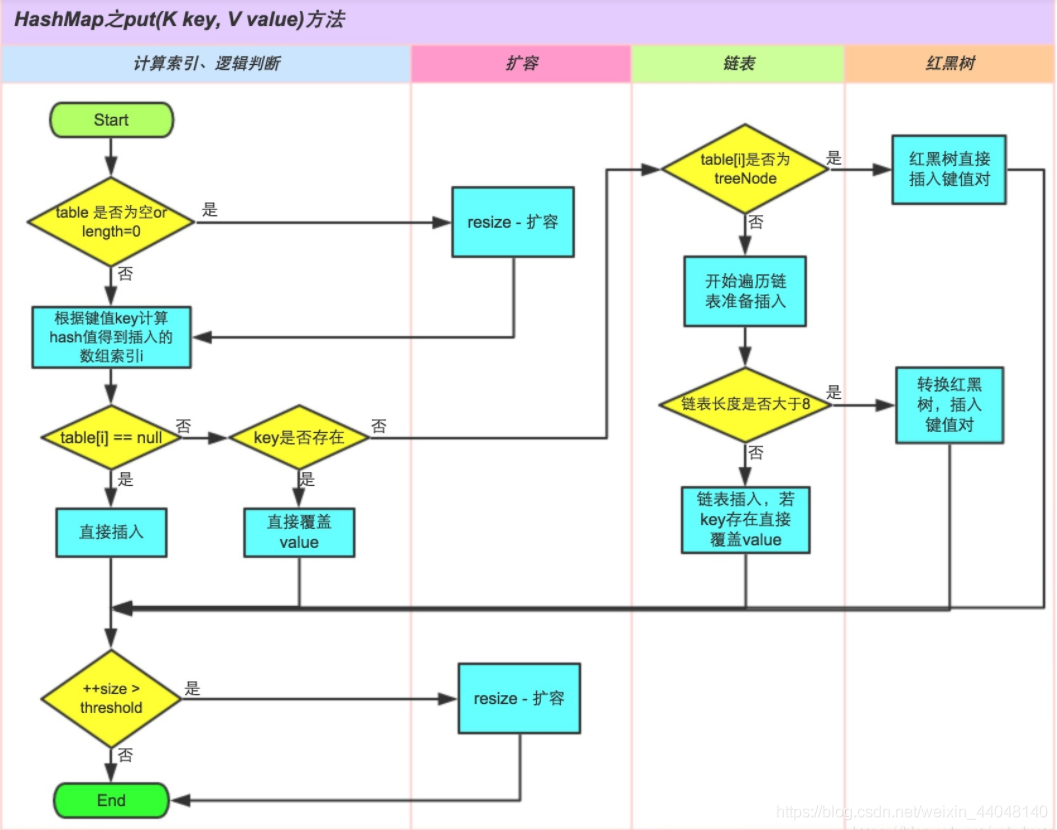
put函数
//调用putVal向当前集合中存放元素并返回对应的val
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
//存放对应的key-val
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
//如果当前集合为null则将集合扩容并且将新的存放结构赋值给tab
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
//找到key存放的链表,如果为空直接将当前节点存放链表在第一个位置
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else { //当前为链表不为null
Node<K,V> e; K k;
//表示当前链表第一个位置key已经存在,将当前节点赋值给e
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
//查看当前的节点是否属于树形结构如果是则在TreeNode中查找并将赋值给e
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) {
//找到当前存放位置节点的最后一个节点的next并将当前要插入的节点插入
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // 链表的长度为8的时候转化为红黑树减一是因为元素从0开始
treeifyBin(tab, hash);
//跳出死循环
break;
}
//表示的是当前链表已经存在当前要插入的key,HashMap不存在重复的key
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
//将节点后移
p = e;
}
}
if (e != null) { // 当前节点不为null将e.val存放在oldValue
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)//不管oldValue是否为null都会发生value赋值给e.value
//当出现重复的key之后上面会将节点保存给e并未修改新的val值,在此更新
e.value = value;
//将结点向后调整到最后面
afterNodeAccess(e);
//如果为null返回null,不为null返回对应的val
return oldValue;
}
}
//++modCount对其集合操作的次数+1
++modCount;
if (++size > threshold)//如果在放入元素以后大于阈值则进行2倍扩容
resize();
afterNodeInsertion(evict);
return null;
}
resize函数
//将集合扩容
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
//旧表的容量
int oldCap = (oldTab == null) ? 0 : oldTab.length;
//之前的阈值
int oldThr = threshold;
int newCap, newThr = 0;
//这里也可以说集合不为空
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {//如果集合现在数组的长度大于等于最大容量
threshold = Integer.MAX_VALUE;//将整型最大的值赋值给threshold
return oldTab;
}
//当前集合数组长度扩大二倍赋值给newCap小于MAXIMUM_CAPACITY
//并且集合的容量大于等于默认容量将当前阈值扩大二倍赋值给新的阈值
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
//若没有经历过初始化,通过构造函数指定了initialCapcity,将当前容量设置为大于它最小的2的n次方
else if (oldThr > 0)
newCap = oldThr;
else { // 初始的时候长度和阈值都使用默认值
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
//重新计算threshold
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
//更新当前集合阈值
threshold = newThr;
//从这里开始便是将oldTab数据重新hash放入扩容后的newTab
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
//将table指向的oldTab指向newTab
table = newTab;
if (oldTab != null) {
//遍历哈希表
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
//当前链表是否为null、并且将就链表赋值给e
if ((e = oldTab[j]) != null) {
oldTab[j] = null;//将原来位置的链表置为null方便垃圾回收
if (e.next == null)//链表的长度为1直接将链表中的一个节点重新hash存放到相应的位置
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode) //表示节点类型为树形结构
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { //链表是非树形结构,并且节点数量是大于1
//将链表拆分为两个子链表
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do { //通过do...while遍历链表
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null) //设置头节点
loHead = e;
else //设置尾结点
loTail.next = e;
loTail = e;//将尾结点变为最后一个节点
}
else {
if (hiTail == null)//同上都是设置头节点下面也一样是设置尾结点
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {//在新表的j位置存放链表
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {//在新表的j+oldCap位置存放链表
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
remove函数
// 移除指向key返回对应的val
public V remove(Object key) {
Node<K,V> e;
//返回如果为空返回null否则返回e.val
return (e = removeNode(hash(key), key, null, false, true)) == null ?
null : e.value;
}
final Node<K,V> removeNode(int hash, Object key, Object value,
boolean matchValue, boolean movable) {
Node<K,V>[] tab; Node<K,V> p; int n, index;
//常规的判断表不为null,key有对应的存储位置
if ((tab = table) != null && (n = tab.length) > 0 &&
(p = tab[index = (n - 1) & hash]) != null) {
Node<K,V> node = null, e; K k; V v;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
//表示的是key存储在当前链表的第一个位置
node = p;
else if ((e = p.next) != null) {//表示的是链表的长度大于1
if (p instanceof TreeNode)//判断是否是树的实列
//返回对应key在红黑树存储的位置
node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
else {//当前结构为链表
do {//遍历链表
if (e.hash == hash &&
((k = e.key) == key ||
(key != null && key.equals(k)))) {//找到对应的节点保存并跳出循环
node = e;
break;
}
//将节点后移
p = e;
} while ((e = e.next) != null);
}
}
//表示要删除的key存在并且找到
if (node != null && (!matchValue || (v = node.value) == value ||
(value != null && value.equals(v)))) {
if (node instanceof TreeNode)//如果是树形在树型结构中移除当前节点
((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
else if (node == p)//表示的链表中的第一个节点
tab[index] = node.next;
else
p.next = node.next;//移除节点
++modCount;//操作+1
--size;//长度-1
afterNodeRemoval(node);
//返回节点
return node;
}
}
return null;
}
clear函数
//清除集合中的所有key-value
public void clear() {
Node<K,V>[] tab;
//集合操作+1
modCount++;
if ((tab = table) != null && size > 0) {//表不为null才进行遍历
size = 0;
for (int i = 0; i < tab.length; ++i)//遍历集合所有元素都置为null,方便垃圾回收
tab[i] = null;
}
}
containsValue函数
//查看集合是否包含指定value
public boolean containsValue(Object value) {
Node<K,V>[] tab; V v;
if ((tab = table) != null && size > 0) {//表不为null
for (int i = 0; i < tab.length; ++i) {//遍历数组
for (Node<K,V> e = tab[i]; e != null; e = e.next) {//遍历链表
if ((v = e.value) == value ||
(value != null && value.equals(v)))
//存在指定的value直接返回true
return true;
}
}
}
//集合中不存在指定value返回false
return false;
}
keySet函数
//返回key的所有集合set
public Set<K> keySet() {
Set<K> ks = keySet;
if (ks == null) {
ks = new KeySet();
keySet = ks;
}
return ks;
}
values函数
//返回所有的value集合
public Collection<V> values() {
Collection<V> vs = values;
if (vs == null) {
vs = new Values();
values = vs;
}
return vs;
}
entrySet函数
// 返回所有的key-value集合
public Set<Map.Entry<K,V>> entrySet() {
Set<Map.Entry<K,V>> es;
return (es = entrySet) == null ? (entrySet = new EntrySet()) : es;
}
面试常见的问题
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
本文链接:
https://blog.csdn.net/weixin_44048140/article/details/116133070
锋哥最新SpringCloud分布式电商秒杀课程发布
👇👇👇
👆长按上方微信二维码 2 秒
感谢点赞支持下哈 
评论