小白之通俗易懂的贝叶斯定理
加入极市专业CV交流群,与 10000+来自港科大、北大、清华、中科院、CMU、腾讯、百度 等名校名企视觉开发者互动交流!
同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总,行业技术交流。关注 极市平台 公众号 ,回复 加群,立刻申请入群~
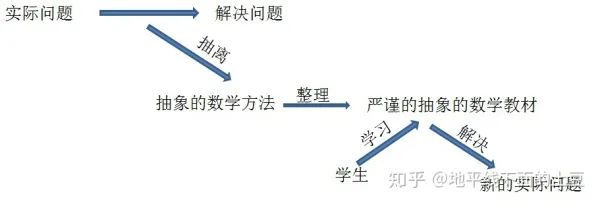
1、祖先是遇到具体的实际问题,然后解决问题,提取方法,整理成抽象的严谨的理论。
2、而后人是学习抽象的严谨的理论,并利用这些理论去解决新的具体的实际的问题。
1、贝叶斯定理的产生来源


2、什么是贝叶斯定理?
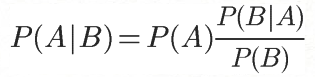
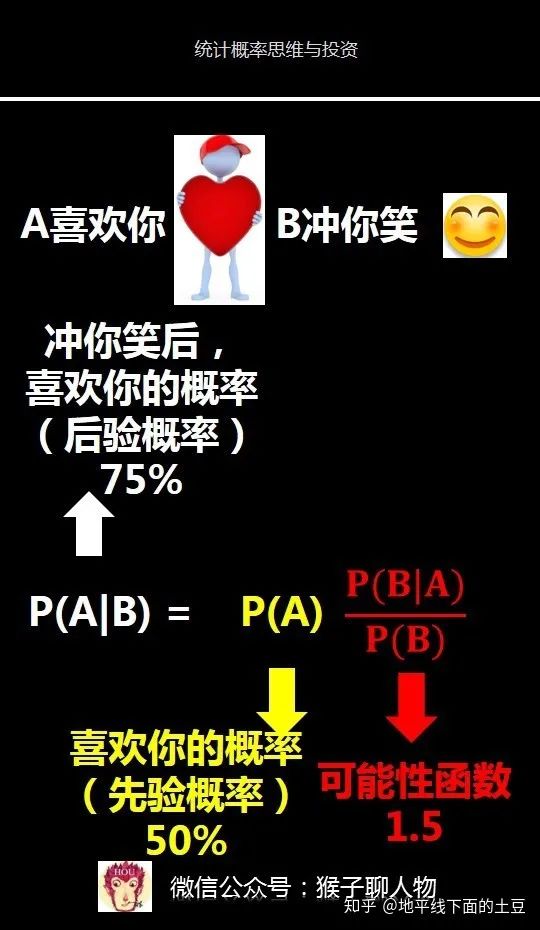
1)要求解的问题:女神喜欢你,记为A事件
2)已知条件:女神经常冲你笑,记为B事件
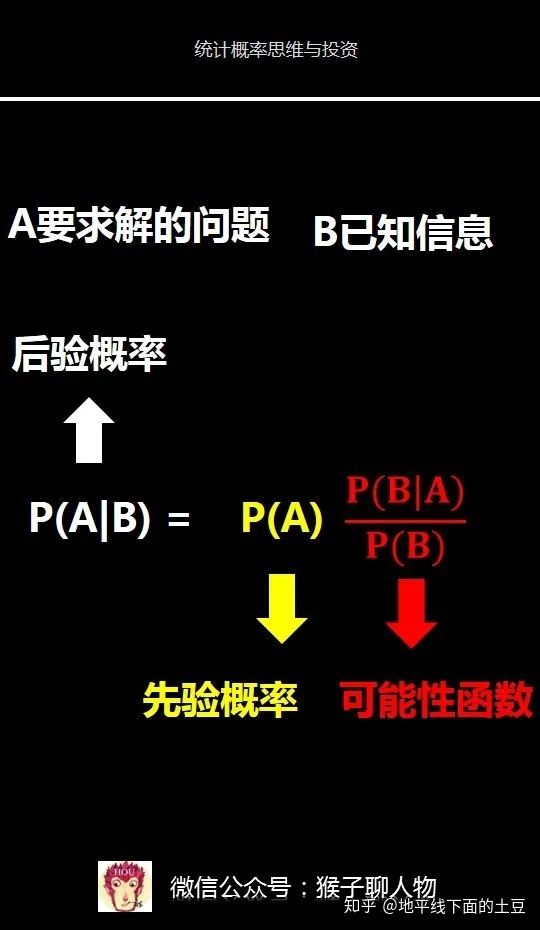
我们把P(A)称为"先验概率"(Prior probability),即在不知道B事件发生的前提下,我们对A事件发生概率的一个主观判断。这个例子里就是在不知道女神经常对你笑的前提下,来主观判断出女神喜欢一个人的概率。这里我们假设是50%,也就是有可能喜欢你,也有可能不喜欢还你的概率各是一半。
P(B|A)/P(B)称为**"可能性函数"(Likelyhood),这是一个调整因子,即新信息事件B的发生调整,作用是,使得先验概率更接近真实概率。**
如果"可能性函数"=1,意味着B事件无助于判断事件A的可能性;
如果"可能性函数"<1,意味着"先验概率"被削弱,事件A的可能性变小。
P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。这个例子里就是在女神冲你笑后,对女神喜欢你的概率重新预测。
带入贝叶斯公式计算出P(A|B)=P(A)* P(B|A)/P(B)=50% *1.5=75%
我们先根据以往的经验预估一个"先验概率"P(A),然后加入新的信息(实验结果B),这样有了新的信息后,我们对事件A的预测就更加准确。
后验概率(新信息出现后A发生的概率)=先验概率(A发生的概率)x可能性函数(新信息带出现来的调整)
如果我能掌握一个事情的全部信息,我当然能计算出一个客观概率(古典概率、正向概率)。
可是生活中绝大多数决策面临的信息都是不全的,我们手中只有有限的信息。既然无法得到全面的信息,我们就在信息有限的情况下,尽可能做出一个好的预测。也就是,在主观判断的基础上,可以先估计一个值(先验概率),然后根据观察的新信息不断修正(可能性函数)。
3、贝叶斯定理的应用案例
为了后面的案例计算,我们需要先补充下面这个知识。
1.全概率公式
这个公式的作用是计算贝叶斯定理中的P(B)。
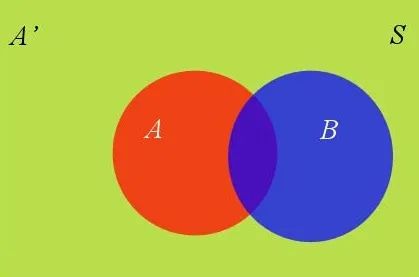
假定样本空间S,由两个事件A与A'组成的和。例如下图中,红色部分是事件A,绿色部分是事件A',它们共同构成了样本空间S。

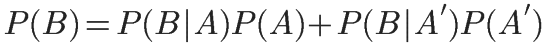
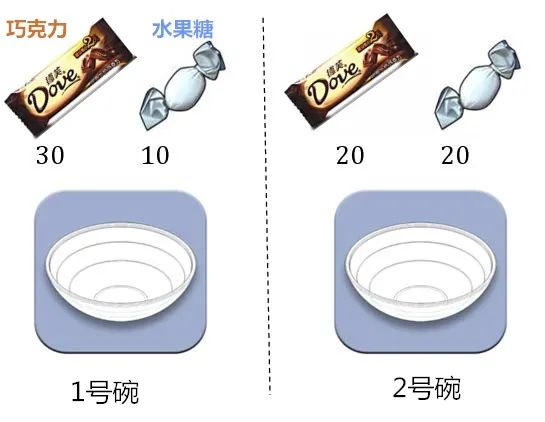
有两个一模一样的碗,1号碗里有30个巧克力和10个水果糖,2号碗里有20个巧克力和20个水果糖。
问题:这颗巧克力来自1号碗的概率是多少?
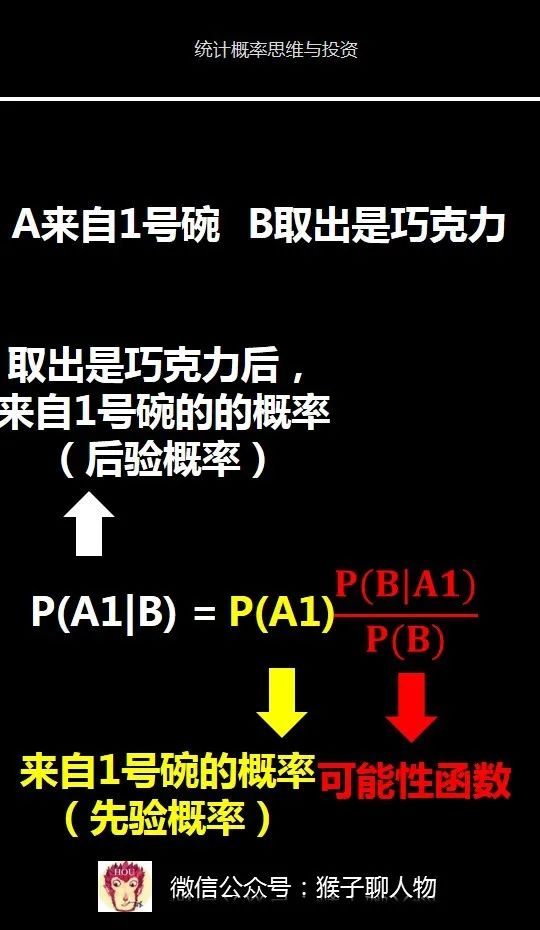
1)要求解的问题:取出的巧克力,来自1号碗的概率是多少?
来自1号碗记为事件A1,来自2号碗记为事件A2
取出的是巧克力,记为事件B,
那么要求的问题就是P(A1|B),即取出的是巧克力,来自1号碗的概率
2)已知信息:
1号碗里有30个巧克力和10个水果糖
2号碗里有20个巧克力和20个水果糖
取出的是巧克力
由于两个碗是一样的,所以在得到新信息(取出是巧克力之前),这两个碗被选中的概率相同,因此P(A1)=P(A2)=0.5,(其中A1表示来自1号碗,A2表示来自2号碗)
这个概率就是"先验概率",即没有做实验之前,来自一号碗、二号碗的概率都是0.5。
P(B|A1)/P(B)
其中,P(B|A1)表示从一号碗中(A1)取出巧克力(B)的概率。
因为1号碗里有30个水果糖和10个巧克力,所以P(B|A1)=30/(30+10)=75%
现在只有求出P(B)就可以得到答案。根据全概率公式,可以求得P(B)如下图:
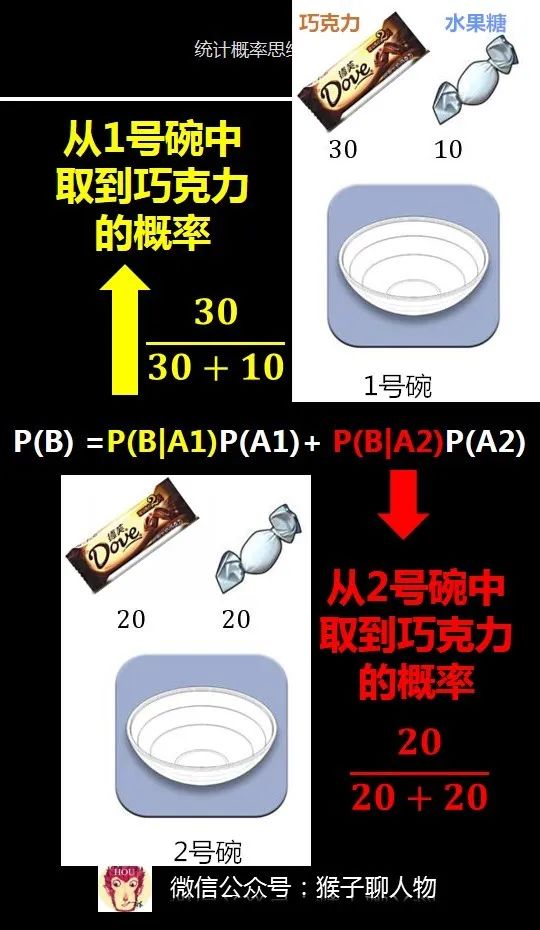
同样的,P(B|A2)是2号碗中巧克力的概率,也很容易求出(图中已给出)。
而P(A1)=P(A2)=0.5
将这些数值带入公式中就是小学生也可以算出来的事情了。最后P(B)=62.5%
可能性函数>1.表示新信息B对事情A1的可能性增强了。
将上述计算结果,带入贝叶斯定理,即可算出P(A1|B)=60%
这个例子中我们需要关注的是约束条件:抓出的是巧克力。如果没有这个约束条件在,来自一号碗这件事的概率就是50%了,因为巧克力的分布不均把概率从50%提升到60%。

第1步. 分解问题
简单来说就像做应用题的感觉,先列出解决这个问题所需要的一些条件,然后记清楚哪些是已知的,哪些是未知的。
1)要求解的问题是什么?
识别出哪个是贝叶斯中的事件A(一般是想要知道的问题),哪个是事件B(一般是新的信息,或者实验结果)
2)已知条件是什么?
第3步,求贝叶斯公式中的2个指标
1)求先验概率
2)求可能性函数
3)带入贝叶斯公式求后验概率

每一个医学检测,都存在假阳性率和假阴性率。所谓假阳性,就是没病,但是检测结果显示有病。假阴性正好相反,有病但是检测结果正常。
但我们用贝叶斯分析算一下,你会发现你的直觉是错误的。
1)要求解的问题:病人的检验结果为阳性,他确实得病的概率有多大?
病人的检验结果为阳性(新的信息)为事件B,他得病记为事件A,
那么求解的就是P(A|B),即病人的检验结果为阳性,他确实得病的概率
2)已知信息
疾病的发病率是0.001,即P(A)=0.001
试剂可以检验患者是否得病,准确率是0.99,即在患者确实得病的情况下(A),它有99%的可能呈现阳性(B),
也就是P(B|A)=0.99
试剂的误报率是5%,即在患者没有得病的情况下,它有5%的可能呈现阳性
得病我们记为事件A,那么没有得病就是事件A的反面,记为A',所以这句话就是P(B|A')=5%

疾病的发病率是0.001,即P(A)=0.001
2)求可能性函数
P(B|A)/P(B)
现在只有求出P(B)就可以得到答案。根据全概率公式,可以求得P(B)=0.05如下图:

3)带入贝叶斯公式求后验概率
我们得到了一个惊人的结果,P(A|B)等于1.98%。
也就是说,筛查的正确性都到了99%以上了,通过体检判断有没有得病的概率也只有1.98%

所以解决的办法倒也很简单,就是先锁定可疑的样本,比如10000人中检查出现问题的那10个人,再独立重复检测一次,因为正常人连续两次体检都出现误测的概率极低,这时筛选出真正患者的准确率就很高了,这也是为什么许多疾病的检测,往往还要送交独立机构多次检查的原因。
垃圾邮件是一种令人头痛的问题,困扰着所有的互联网用户。全球垃圾邮件的高峰出现在2006年,那时候所有邮件中90%都是垃圾,2015年6月份全球垃圾邮件的比例数字首次降低到50%以下。
最初的垃圾邮件过滤是靠静态关键词加一些判断条件来过滤,效果不好,漏网之鱼多,冤枉的也不少。
2002年,Paul Graham提出使用"贝叶斯推断"过滤垃圾邮件。他说,这样做的效果,好得不可思议。1000封垃圾邮件可以过滤掉995封,且没有一个误判。
4、生活中的贝叶斯思维
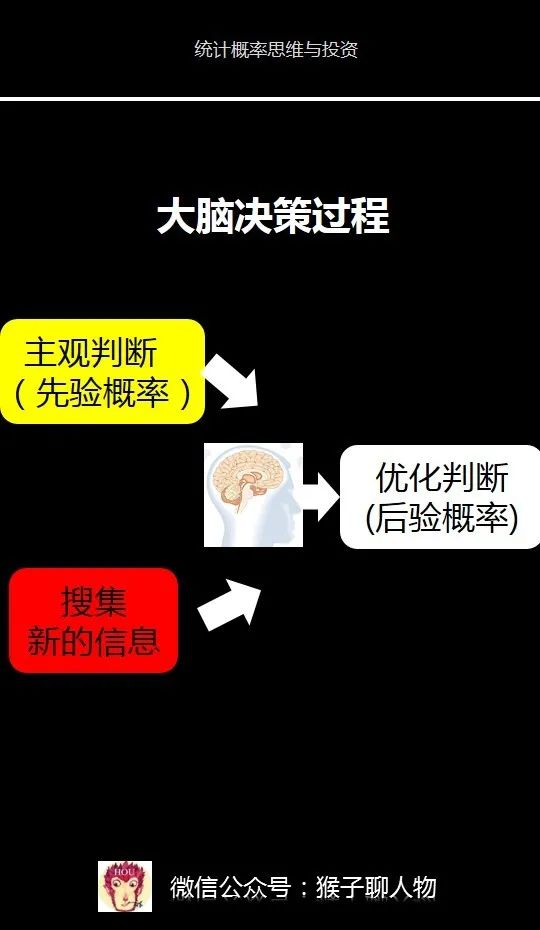
简单来说就像小学生做应用题的感觉,先列出要解决的问题是什么?已知条件有哪些?
不是瞎猜,而是根据自己的经历和学识来给出一个主观判断。
持续关于你要解决问题相关信息的最新动态,然后用获取到的新信息来不断调整第2步的主观判断。如果新信息符合这个主观判断,你就提高主观判断的可信度,如果不符合,你就降低主观判断的可信度。
推荐阅读

评论
