如何 Get 机器学习必备的数学技能?(文末赠书)
1
数学对机器学习与深度学习的重要性
数学。这两本书里密集的出现数学概念和公式,对大部分读者来说都是很困难的,尤其是不少数学知识超出了理工科本科“微积分”,“线性代数”,“概率论与数理统计”3门课的范围。陌生的数学符号和公式让大家茫然不知所措。 机器学习和深度学习中的一些思想不易理解。有些复杂的算法,比如支持向量机、反向传播算法、EM算法、概率图模型、变分推断,它们到底解决了什么问题,为什么要这样做,这些书里解释的不太清楚,这就造成了读者不知其所以然。 抽象。有些机器学习算法是很抽象的,比如流形学习、谱聚类算法等。如果不给出直观的解释,也是难以理解的。 不能和应用结合。很多教材普遍存在的一个问题是没有讲清楚这个方法到底有什么用,应该怎么用。
2
西瓜书中的数学
最优化方法
信息论
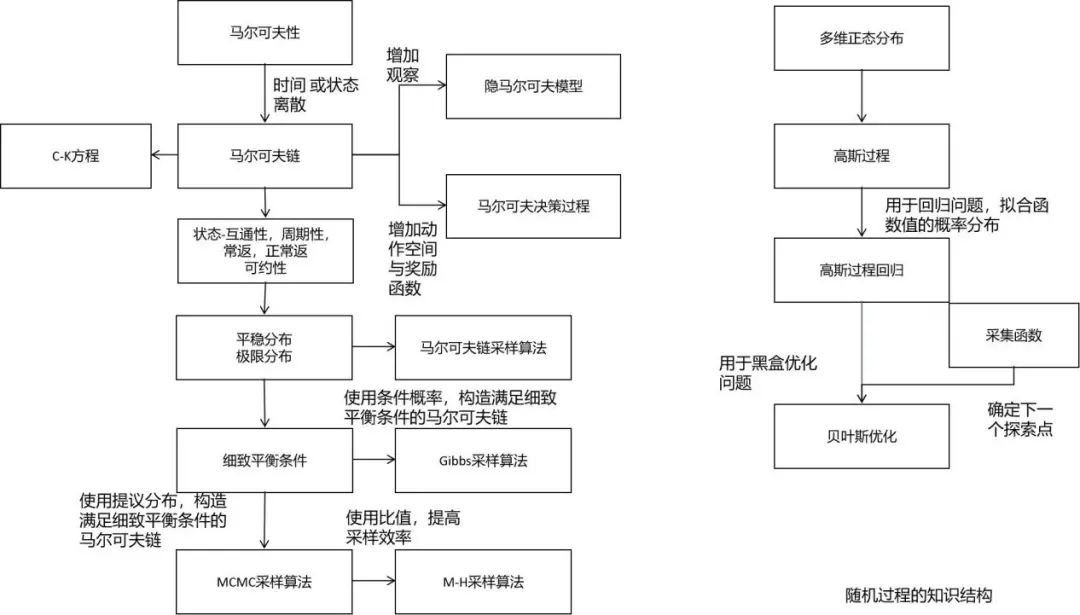
随机过程
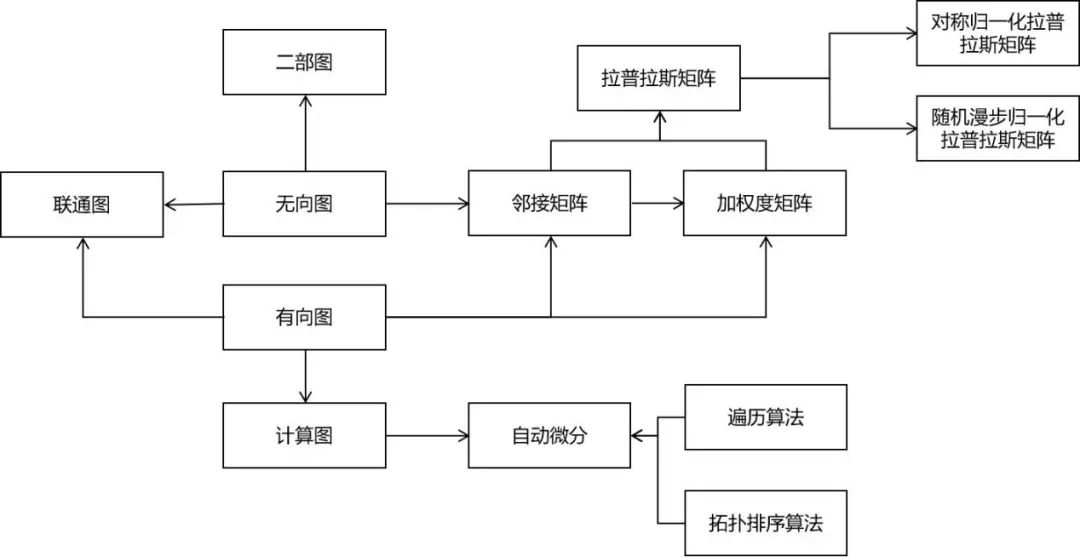
图论
3
花书中的数学
线性代数
概率论与信息论
数值计算
线性因子模型
自编码器
表示学习
深度学习中的结构化概率模型
蒙特卡洛方法
直面配分函数
近似推断
深度生成模型
MCMC采样算法;
EM算法;
近似推断和变分推断;
变分法;
RBM的训练算法
最优化方法
信息论
随机过程
图论

4
究竟需要哪些数学知识
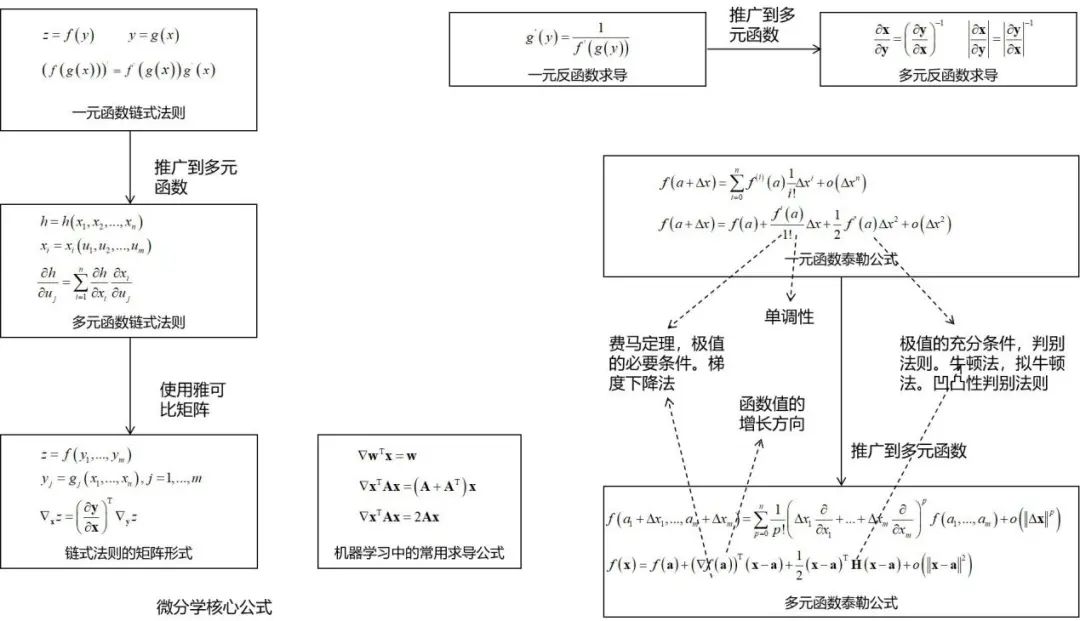
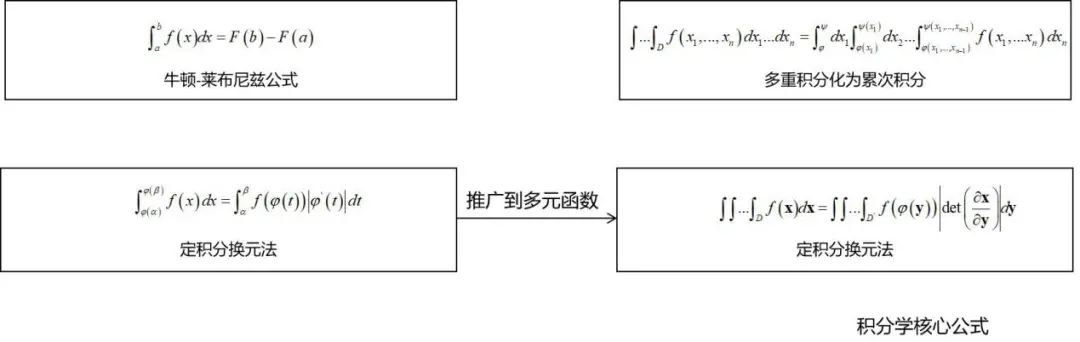
微积分
线性代数
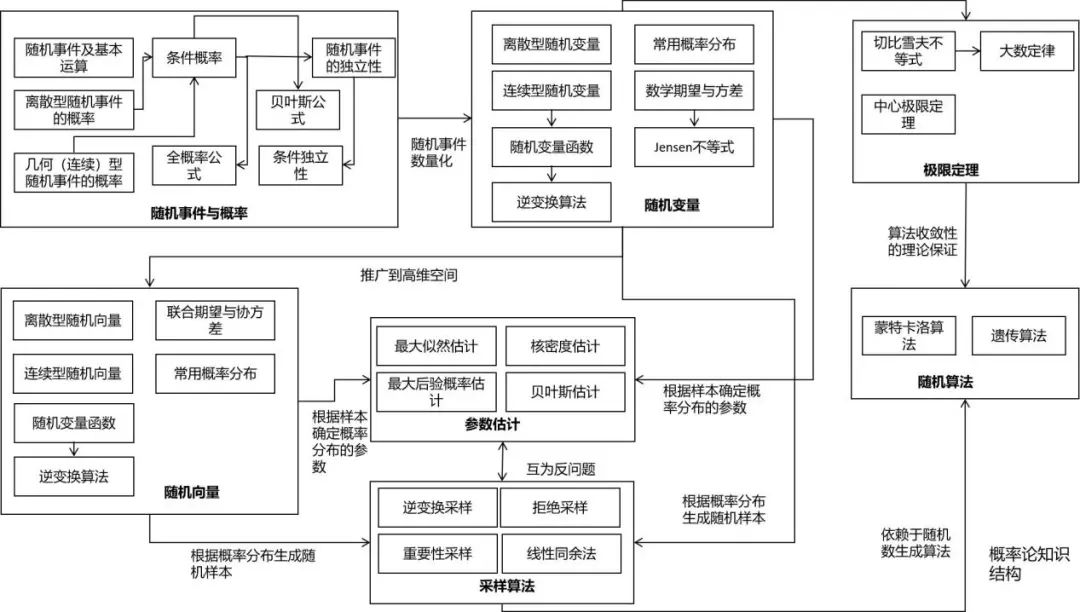
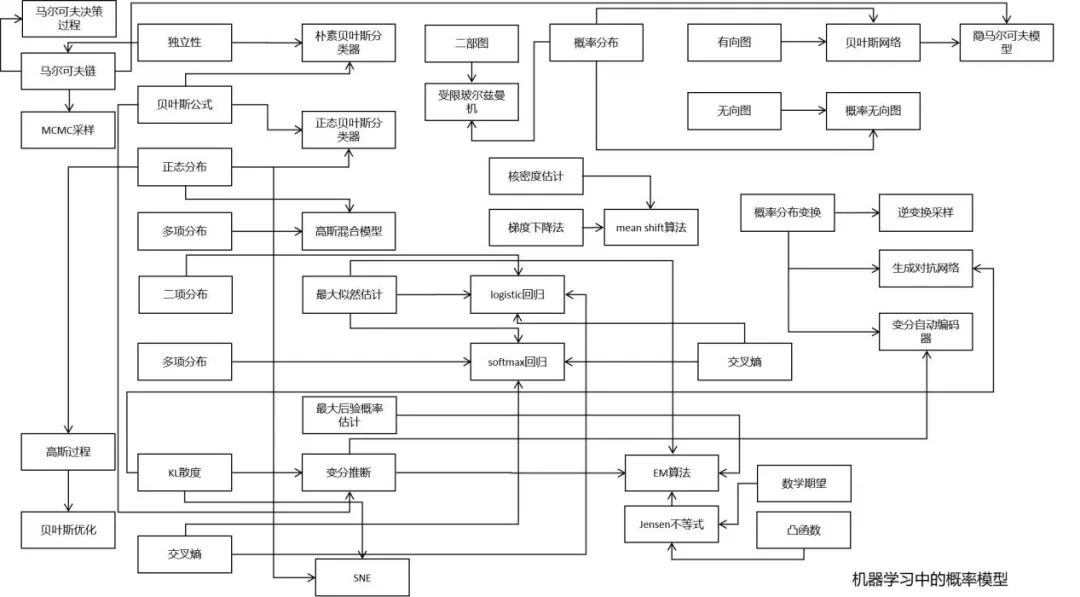
概率论
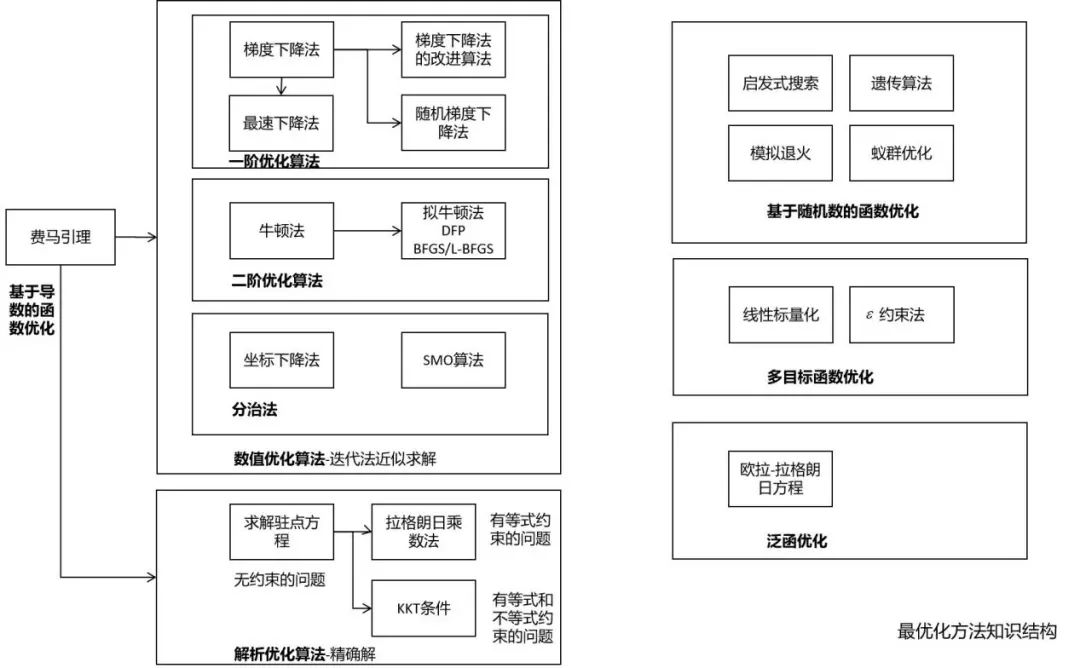
最优化方法
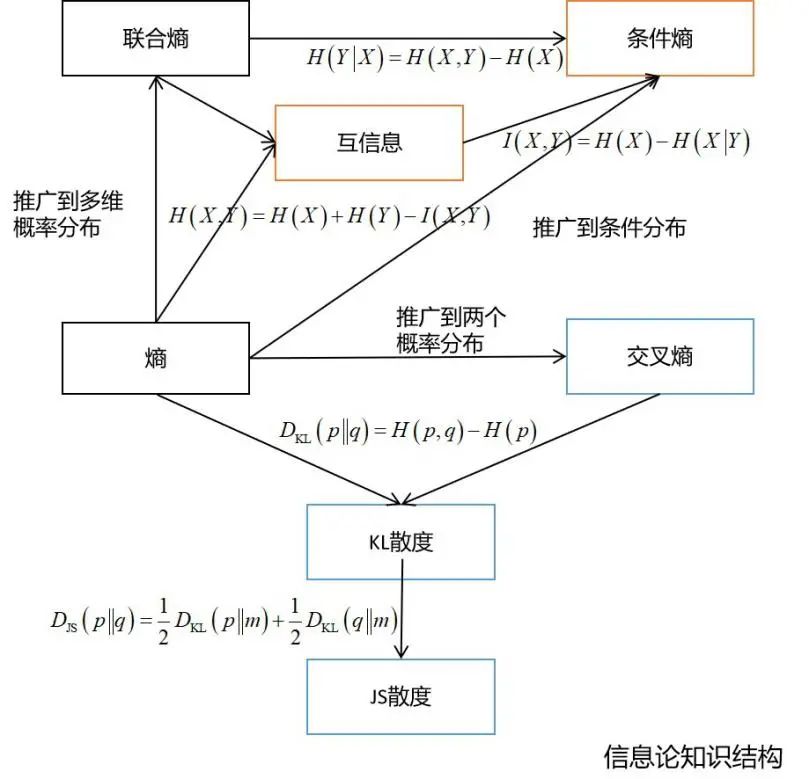
信息论
随机过程
图论
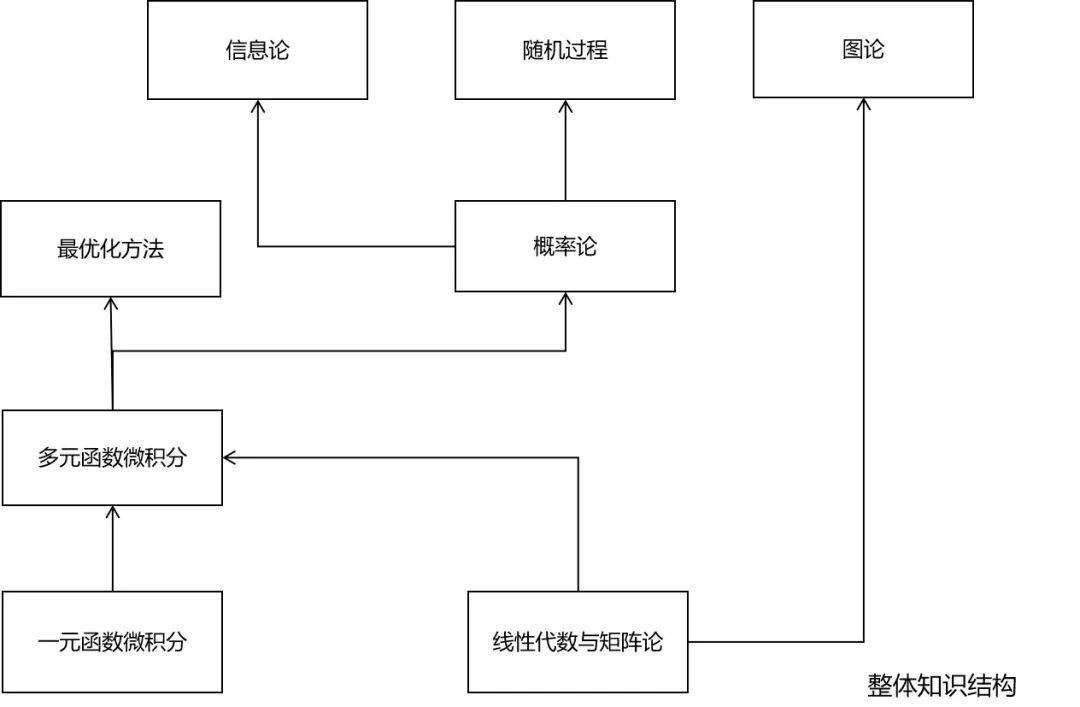
微积分
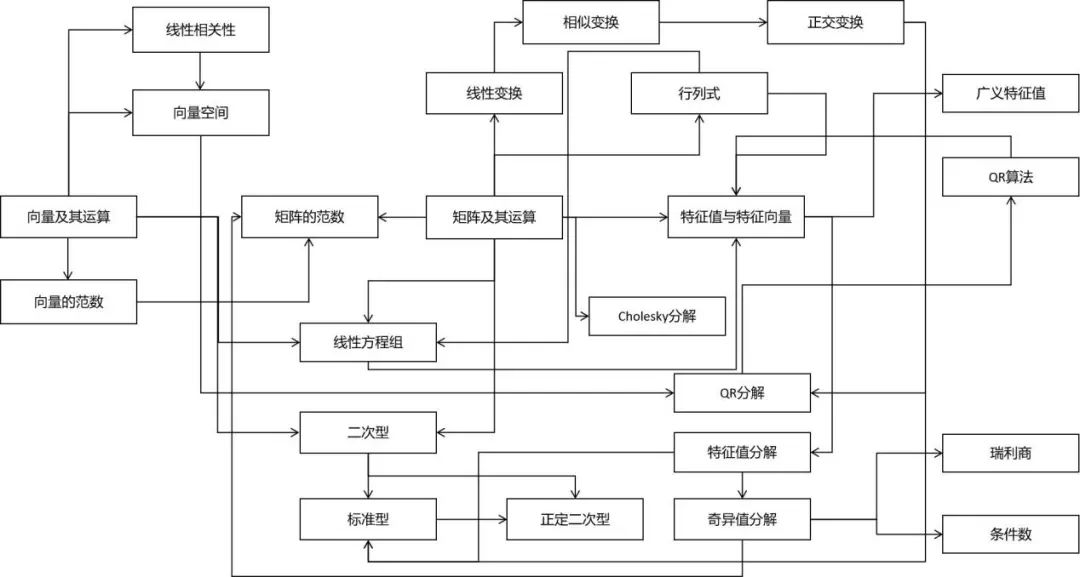
决策树的训练过程中需要使用熵作为指标 在深度学习中经常会使用交叉熵、KL散度、JS散度、互信息等概念 变分推断的推导需要以KL散度为基础 距离度量学习、流形降维等算法也需要信息论的知识
4
《机器学习的数学》是你的一个好选择
使用图/表等方式降低理解难度。
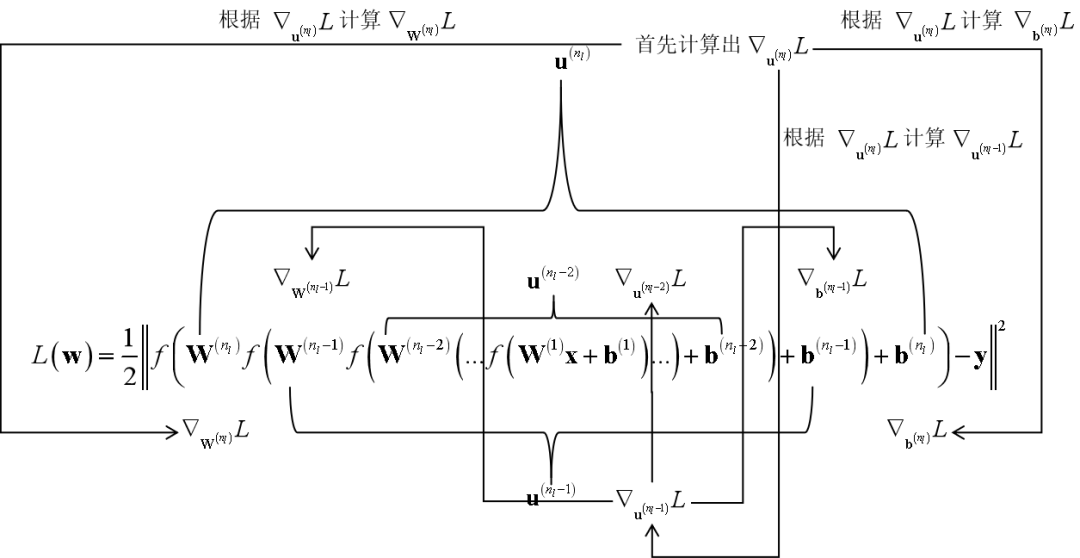
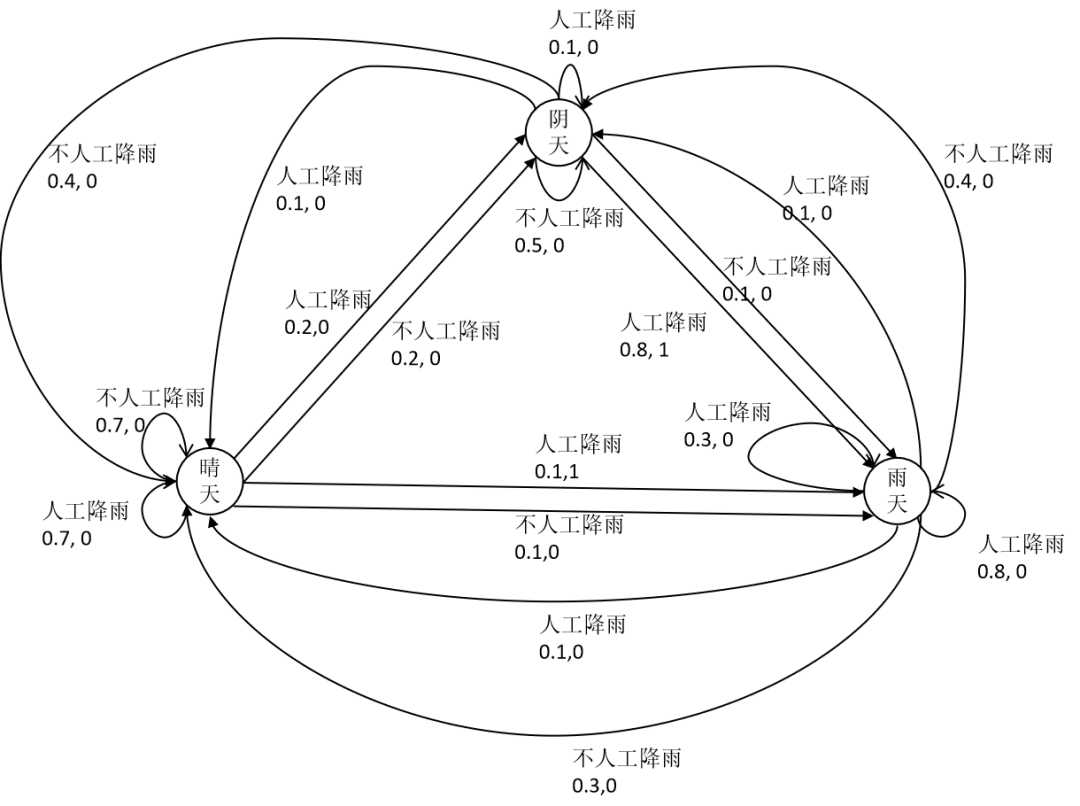
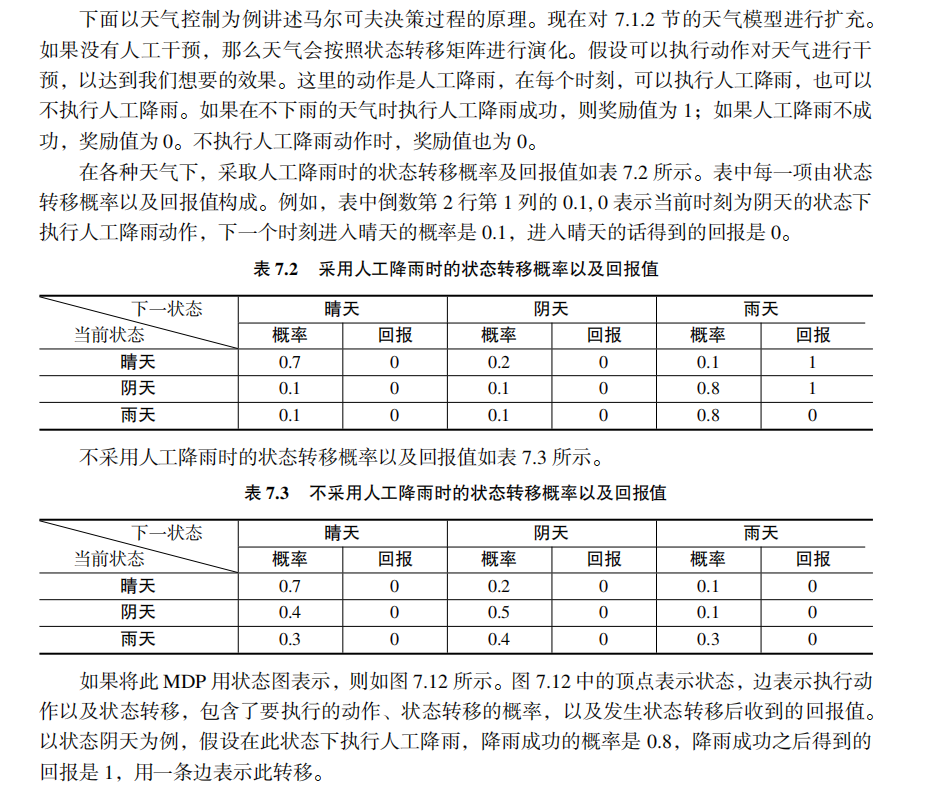
强化学习中为什么需要用马尔可夫决策过程进行建模? 为什么需要用状态转移概率? 为什么奖励函数与状态转移有关? 确定性策略,非确定性策略到底是怎么回事?
为什么用Householder变换可以将矩阵变换为近似对角的矩阵? Householder变换的变换矩阵是怎样构造的,为什么要这么构造? 为何不直接将对称矩阵变换为对角矩阵?


4
配套的高质量课程
分享
收藏
点赞
在看

评论
