线扫描结构光较之面阵结构光较为简单,精度也比较高,在工业中广泛用于物体体积测量、三维成像等领域。
通过上图可以看到线扫描结构光装置的一个基本结构。主动光源L缓慢扫过待测物体,在此过程中,相机记录对应的扫描过程,最后,依据相机和光源在该过程中的相对位姿和相机内参等参数,就可以重建出待测物体的三维结构。 其中, 为投影装置的朝向。 则需要通过对应像素的像素坐标 和焦距f来确定。最终可知P点的三维坐标为: 可以看到,三维空间中的情形和之前的二维空间类似,作为俯仰角的 并没有出现在公式中。 如上图,相机与投影器等相对位姿都经过了精确的校正,并且选取了测量台上的一角作为原点建立物方坐标系。因此,激光投影器所投射的线激光在物方坐标系中可以通过一个平面方程来描述: 而相机光心的位姿通过几何校正也已知,可以通过找到线激光在图像中的对应像素重建出光心与像素的射线,射线和激光平面的交点即为待求的三维空间点。 面阵结构光大致可以分为两类:随机结构光 和编码结构光 。随机结构光较为简单,也更加常用。通过投影器向被测空间中投射亮度不均 和随机分布 的点状结构光,通过双目相机成像,所得的双目影像经过极线校正后再进行双目稠密匹配,即可重建出对应的深度图。如下图为某种面阵的红外结构光。 随机结构光这里就不再说了,因为和普通双目算法是很相似的。一些额外的考虑就是是否给相机加装滤光片、光斑的密度要到什么程度等硬件和光学的问题了。 如上图,时序编码结构光即为在一定时间范围内,通过投影器向被测空间投射一系列明暗不同的结构光,每次投影都通过相机进行成像。假设共有n张影像,并设被阴影覆盖的部分编码值为1,未被覆盖的部分编码值为0。此时,每个像素都对应唯一一个长度为n的二进制编码,双目影像搜索匹配像素的问题就变成了查找具有相同编码值的像素。如果双目图像已经进行了极线校正,那么所投影的结构光只需要在x方向上不具有重复性即可。 如上图中,红框内的像素的编码为0110,转化为十进制则为5。此时,只需要在右图相同行上检索编码值为5的像素即可。 上图编码方式称为二进制码 (binary code),每段区域不断的进行二分下去直至投影的编码宽度等于相机的像素宽度即可。对于宽度为1024的图像,最少需要10张影像来进行编码。 Binary Code 的一种改进为Gray Code . Gray Code比Binary Code具有更好的鲁棒性,它使得相邻两个像素相差1bit。Gray Code的详细介绍和其与Binary Code之间的转换可以参考 wikipedia 。 注意观察即可看到gray code和binary code在前几行像素上的不同 自然,除了使用二进制的0-1编码之外,还可以使用更多颜色层级的编码。假设使用了M种不同的灰度层级进行编码,则拍摄N张影像可以得到包含 个条带的影响。如下图中M = 3, N = 3时图中有27条条带。 为满足动态场景的需要,可以采用空间编码结构光。前面谈到了随机结构光,就是不带编码信息,投影随机纹理,而这里讨论的空间编码结构光特指向被测空间中投影经过数学编码的、一定范围内的光斑不具备重复性的结构光。由此,某个点的编码值可以通过其临域获得。其中,包含一个完整的空间编码的像素数量(窗口大小)就决定了重建的精度。
2.2.1 德布鲁因序列 (De Bruijn) 序列
德布鲁因序列( 维基百科 )B(k, n) 表示用k个符号(如二进制,k = 2)来表示长度为 的循环编码,n为一个编码值的长度。
举例:最简单的,k = 2时,采用二进制符号(0, 1),编码值的长度n = 2,可以得到一个长度为 的循环序列:[0, 0, 1, 1]。此时,我们得到4个长度为2的不同的编码:[0, 0], [0, 1], [1, 1], [1, 0]. 因此,某种结构光就可以按照该德布鲁因序列进行编码。而获得的结构光影像中,以上4个像素的编码为[0, 0, 1, 1],通过一个大小为2的滑动窗口(假定一个结构光光斑或光束的宽度是一个像素)即可获取每个像素的编码值。同样地,如果是经过极线校正的双目图像,只需要搜索对应的行即可,此时只要求编码在x轴上不具备重复性。此时的结构光就是竖直条带状的。 当然,为了提高编码效率,也可以使用灰度图、彩色图像等比0-1编码具有更多可能编码值的投影方式。例如,对于RGB影像,采用二进制编码(即某种颜色只有 有、无 两种状态),则共有 种颜色组合,去除(0, 0, 0),还剩下7种颜色。因此k = 7, n = 3,这样就可以获得一个长度为343的条带序列。对于这个序列,唯一的约束为:相邻的条带不能为同样的颜色。否则对于解码算法来说很容易造成误差。下图展示了只使用5种颜色(k = 5, n = 3)的结构光序列: 德布鲁因序列是一种一维编码,可以将之扩展到二维空间中,使得对于一个x * y大小的二维空间,其中一个w * h大小的子窗口所包含的编码值在这整个二维编码序列中只出现一次。 如上面中的4 * 6的M-arrays序列中,每个2 * 2大小的窗口所包含的编码值都是唯一的。 同样也可以利用RGB信息来进行二维编码,有相关算法来产生一些伪随机二维编码。如在下图中,左边展示了一个6 * 6大小的二维矩阵,子窗口的大小为3 * 3。算法首先在左上角的3 * 3子窗口中随机填入各种颜色;然后一个3 * 1大小的滑动窗口移动到右端第一个空白处,并随机填入3中颜色;在填入生成的随机颜色前,算法会先验证子窗口的编码的唯一性能不能得到保证,若不能,则会重新生成3中随机颜色;如此循环,只是在竖直方向上滑动窗口的大小变为1 * 3,直至将整个6 * 6矩阵填满。右图则是该算法产生的某种伪随机二维编码的示例。 通过以上对空间编码的讨论,也可以看出空间编码结构光的一些优缺点: 无需多张照片,只需要一对影像即可进行三维重建。可以满足实时处理,用在动态环境中。 易受噪声干扰:由于反光、照明等原因可能导致成像时部分区域等编码信息缺失; 以上是对各种常用的结构光技术的一些介绍。其实,三维重建中最常用的还是随机面阵结构光。通过向空间中投影这样的随机结构光,再结合双目稠密重建,可以获得比单纯使用RGB影像进行三维重建更加可靠和精确的结果。 最后,向对结构光和三维重建感兴趣的同学推荐一个项目:build your own 3D scanner。和名字一样,网站上提供了自己使用触手可及和低成本的设备来DIY一个3D扫描仪所需的一切,包括教程、ppt、代码、数据和其他人的作品展示,感兴趣的同学欢迎动手尝试。
双一流大学研究生团队创建,专注于目标检测与深度学习,希望可以将分享变成一种习惯!

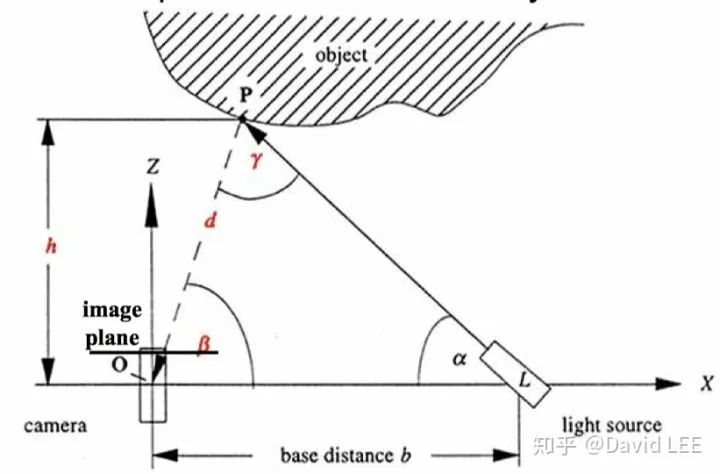


 为投影装置的朝向。
为投影装置的朝向。  则需要通过对应像素的像素坐标
则需要通过对应像素的像素坐标  和焦距f来确定。最终可知P点的三维坐标为:
和焦距f来确定。最终可知P点的三维坐标为:
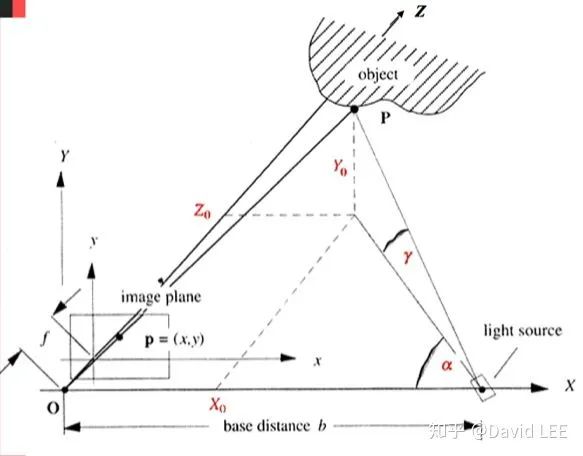




 并没有出现在公式中。
并没有出现在公式中。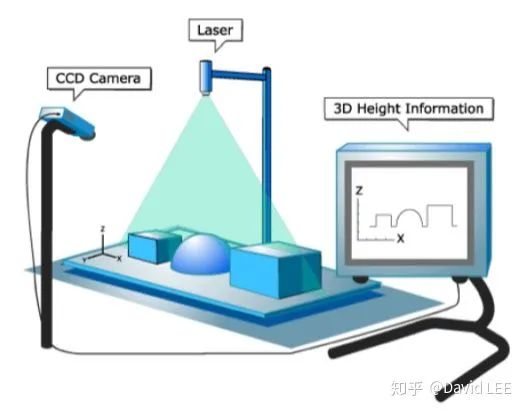










 个条带的影响。如下图中M = 3, N = 3时图中有27条条带。
个条带的影响。如下图中M = 3, N = 3时图中有27条条带。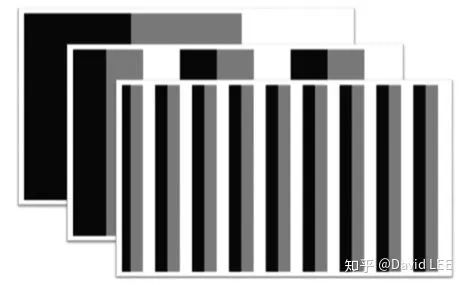
 的循环编码,n为一个编码值的长度。
的循环编码,n为一个编码值的长度。 的循环序列:[0, 0, 1, 1]。此时,我们得到4个长度为2的不同的编码:[0, 0], [0, 1], [1, 1], [1, 0].
的循环序列:[0, 0, 1, 1]。此时,我们得到4个长度为2的不同的编码:[0, 0], [0, 1], [1, 1], [1, 0]. 种颜色组合,去除(0, 0, 0),还剩下7种颜色。因此k = 7, n = 3,这样就可以获得一个长度为343的条带序列。对于这个序列,唯一的约束为:相邻的条带不能为同样的颜色。否则对于解码算法来说很容易造成误差。下图展示了只使用5种颜色(k = 5, n = 3)的结构光序列:
种颜色组合,去除(0, 0, 0),还剩下7种颜色。因此k = 7, n = 3,这样就可以获得一个长度为343的条带序列。对于这个序列,唯一的约束为:相邻的条带不能为同样的颜色。否则对于解码算法来说很容易造成误差。下图展示了只使用5种颜色(k = 5, n = 3)的结构光序列:


