地理空间编码算法之GeoHash
基本原理
通过一个给定的经纬度坐标(经度 146.842813452468、纬度 -54.9432909847213)来介绍该算法的基本原理及流程
基于二分查找的经纬度编码
众所周知,经度范围-180~180,纬度范围-90~90。这里利用二分查找分别计算该经纬度坐标下经度、纬度的编码。其中,位于左区间、右区间的值分别记为0、1。下面即是对经度146.842813452468进行区间二分的过程。这里左区间是左闭右开区间、右区间是左闭右闭区间
-----------------------------------------------------------------------------------------------
左区间 右区间 结果
-----------------------------------------------------------------------------------------------
[-180.000000000000000, 0.000000000000000) [ 0.000000000000000, 180.000000000000000] 1
[ 0.000000000000000, 90.000000000000000) [ 90.000000000000000, 180.000000000000000] 1
[ 90.000000000000000, 135.000000000000000) [ 135.000000000000000, 180.000000000000000] 1
[ 135.000000000000000, 157.500000000000000) [ 157.500000000000000, 180.000000000000000] 0
[ 135.000000000000000, 146.250000000000000) [ 146.250000000000000, 157.500000000000000] 1
[ 146.250000000000000, 151.875000000000000) [ 151.875000000000000, 157.500000000000000] 0
[ 146.250000000000000, 149.062500000000000) [ 149.062500000000000, 151.875000000000000] 0
[ 146.250000000000000, 147.656250000000000) [ 147.656250000000000, 149.062500000000000] 0
[ 146.250000000000000, 146.953125000000000) [ 146.953125000000000, 147.656250000000000] 0
[ 146.250000000000000, 146.601562500000000) [ 146.601562500000000, 146.953125000000000] 1
[ 146.601562500000000, 146.777343750000000) [ 146.777343750000000, 146.953125000000000] 1
[ 146.777343750000000, 146.865234375000000) [ 146.865234375000000, 146.953125000000000] 0
[ 146.777343750000000, 146.821289062500000) [ 146.821289062500000, 146.865234375000000] 1
[ 146.821289062500000, 146.843261718750000) [ 146.843261718750000, 146.865234375000000] 0
[ 146.821289062500000, 146.832275390625000) [ 146.832275390625000, 146.843261718750000] 1
[ 146.832275390625000, 146.837768554687500) [ 146.837768554687500, 146.843261718750000] 1
[ 146.837768554687500, 146.840515136718750) [ 146.840515136718750, 146.843261718750000] 1
[ 146.840515136718750, 146.841888427734380) [ 146.841888427734380, 146.843261718750000] 1
[ 146.841888427734380, 146.842575073242200) [ 146.842575073242200, 146.843261718750000] 1
[ 146.842575073242200, 146.842918395996100) [ 146.842918395996100, 146.843261718750000] 0
-----------------------------------------------------------------------------------------------
我们将每次二分的结果汇总起来,则该经度编码即为:11101000011010111110。同理,我们对纬度-54.9432909847213进行编码,二分过程如下所示
-----------------------------------------------------------------------------------------------
左区间 右区间 结果
-----------------------------------------------------------------------------------------------
[ -90.000000000000000, 0.000000000000000) [ 0.000000000000000, 90.000000000000000] 0
[ -90.000000000000000, -45.000000000000000) [ -45.000000000000000, 0.000000000000000] 0
[ -90.000000000000000, -67.500000000000000) [ -67.500000000000000, -45.000000000000000] 1
[ -67.500000000000000, -56.250000000000000) [ -56.250000000000000, -45.000000000000000] 1
[ -56.250000000000000, -50.625000000000000) [ -50.625000000000000, -45.000000000000000] 0
[ -56.250000000000000, -53.437500000000000) [ -53.437500000000000, -50.625000000000000] 0
[ -56.250000000000000, -54.843750000000000) [ -54.843750000000000, -53.437500000000000] 0
[ -56.250000000000000, -55.546875000000000) [ -55.546875000000000, -54.843750000000000] 1
[ -55.546875000000000, -55.195312500000000) [ -55.195312500000000, -54.843750000000000] 1
[ -55.195312500000000, -55.019531250000000) [ -55.019531250000000, -54.843750000000000] 1
[ -55.019531250000000, -54.931640625000000) [ -54.931640625000000, -54.843750000000000] 0
[ -55.019531250000000, -54.975585937500000) [ -54.975585937500000, -54.931640625000000] 1
[ -54.975585937500000, -54.953613281250000) [ -54.953613281250000, -54.931640625000000] 1
[ -54.953613281250000, -54.942626953125000) [ -54.942626953125000, -54.931640625000000] 0
[ -54.953613281250000, -54.948120117187500) [ -54.948120117187500, -54.942626953125000] 1
[ -54.948120117187500, -54.945373535156250) [ -54.945373535156250, -54.942626953125000] 1
[ -54.945373535156250, -54.944000244140625) [ -54.944000244140625, -54.942626953125000] 1
[ -54.944000244140625, -54.943313598632810) [ -54.943313598632810, -54.942626953125000] 1
[ -54.943313598632810, -54.942970275878906) [ -54.942970275878906, -54.942626953125000] 0
[ -54.943313598632810, -54.943141937255860) [ -54.943141937255860, -54.942970275878906] 0
-----------------------------------------------------------------------------------------------
故,该纬度编码即为:00110001110110111100
合并
对于经度、纬度的编码,我们按照经度、纬度、经度、纬度...顺序,分别依次取一位进行合并。合并结果如下所示

Base32编码
利用下述Base32编码表,对合并后的经纬度编码按5位一组进行编码
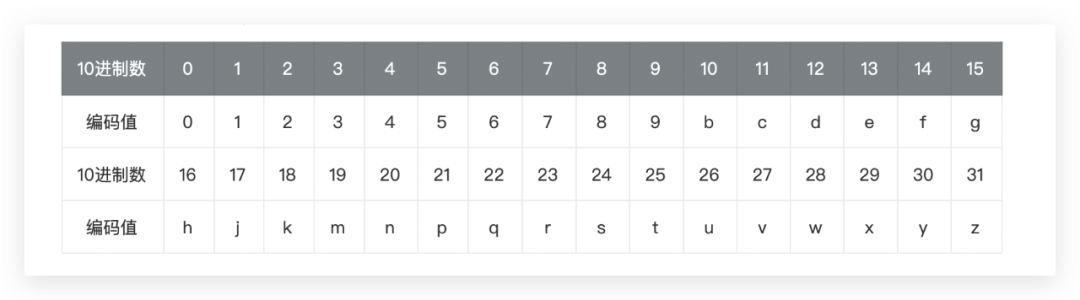
编码过程如下所示
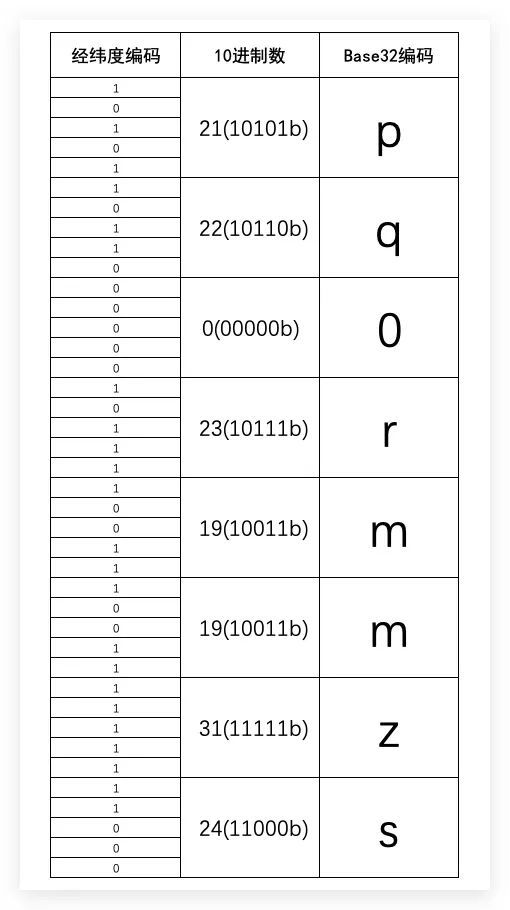
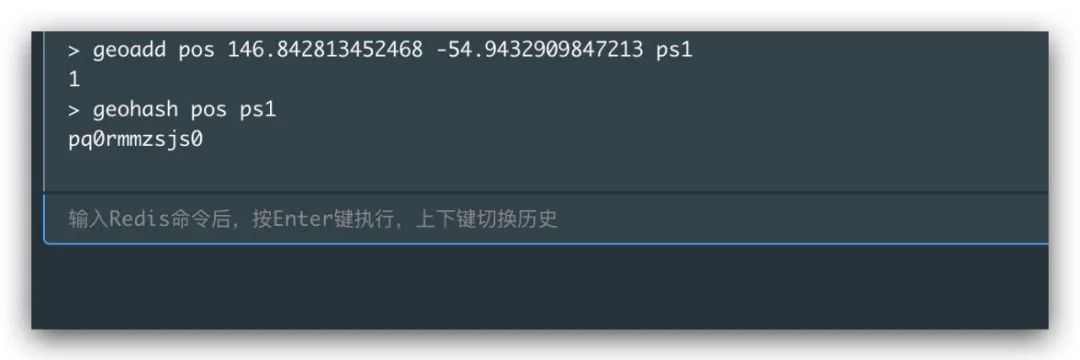
故,最终该经纬度(经度146.842813452468、纬度-54.9432909847213)的GeoHash值即为pq0rmmzs
Note
上文我们提到GeoHash算法计算出来的值实际上表示的是一个矩形网格的区域范围。所以在上述区间二分的过程中,事实上可以不断的持续下去,以获得该经(或纬)度更多位数的编码值,进而缩小该GeoHash值所表示的区域范围,从而能更准确的反映出该经纬度坐标的位置
如果两个网格的GeoHash值共同前缀越长,说明这两个网格区域越接近。这也是为什么在地理信息空间通常将经纬度坐标转换为GeoHash值可以提高查询、检索效率(前缀匹配)。但反之并不成立,即两个很接近的网格区域,可能GeoHash值的共同前缀很短甚至完全没有共同前缀。即所谓的边缘场景,例如两个很邻近的区域如果分别在格林威治子午线(经度为0)的两侧,显然它们的GeoHash值完全没有共同的前缀
GeoHash算法,事实上是空间填充曲线中Z阶曲线(Z-Order Curve)的一种典型应用
对于Redis而言,其从3.2开始增加了对空间地理位置的支持,提供了GeoHash数据类型。下面即是一个利用geoadd、geohash命令计算经纬度坐标的GeoHash值示例