引言

本着“凡我不能创造的，我就不能理解”的思想，本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架，该框架类似PyTorch能实现自动求导。

要深入理解深度学习，从零开始创建的经验非常重要，从自己可以理解的角度出发，尽量不适用外部完备的框架前提下，实现我们想要的模型。本系列文章的宗旨就是通过这样的过程，让大家切实掌握深度学习底层实现，而不是仅做一个调包侠。

本文介绍常见运算的计算图。

计算图直观地表示了计算过程。通过观察反向传播的梯度流动，可以帮助我们理解反向传播的推导过程。

我们会利用计算图来实现自动求导工具。首先我们看一下常见运算操作的计算图。

加法

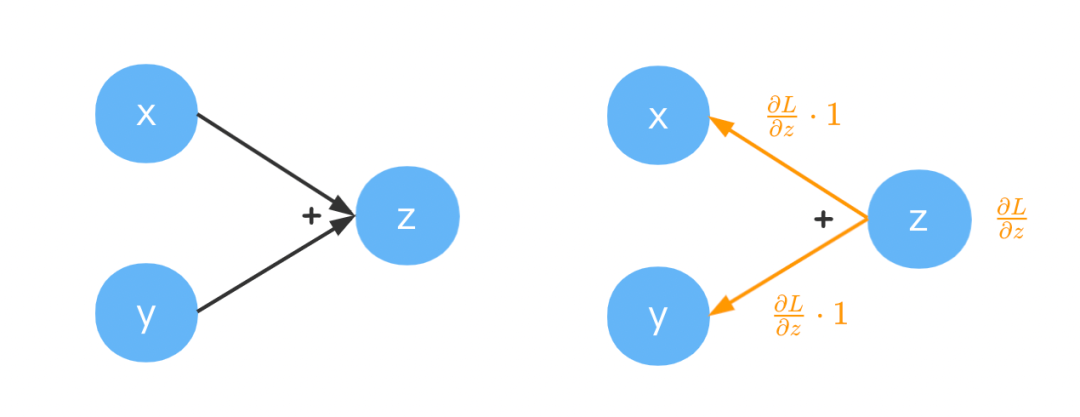
求这个运算的梯度比较简单，易得

为经过反向传播传递到节点上的梯度。

减法

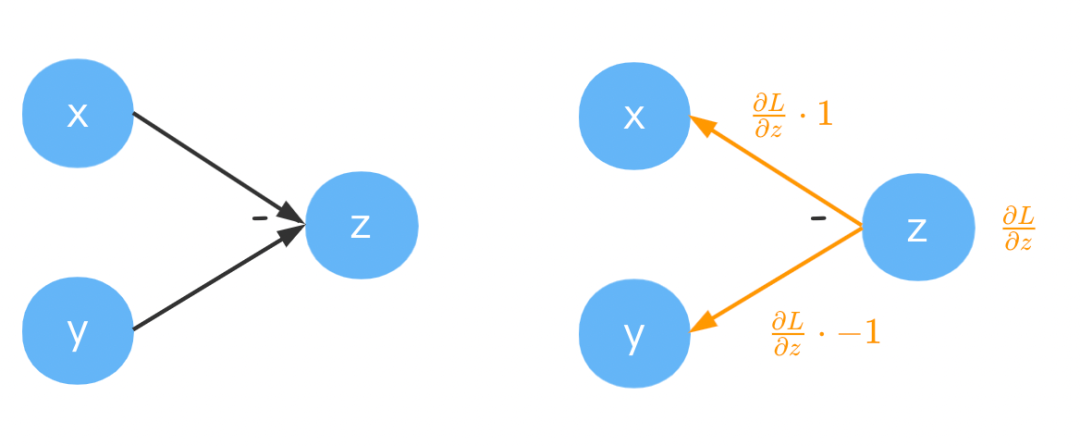
由 可得

乘法

 的梯度也比较简单，易得。

此时，反向传播时会将上游传来的梯度乘以当前路径上计算出来的梯度。

除法

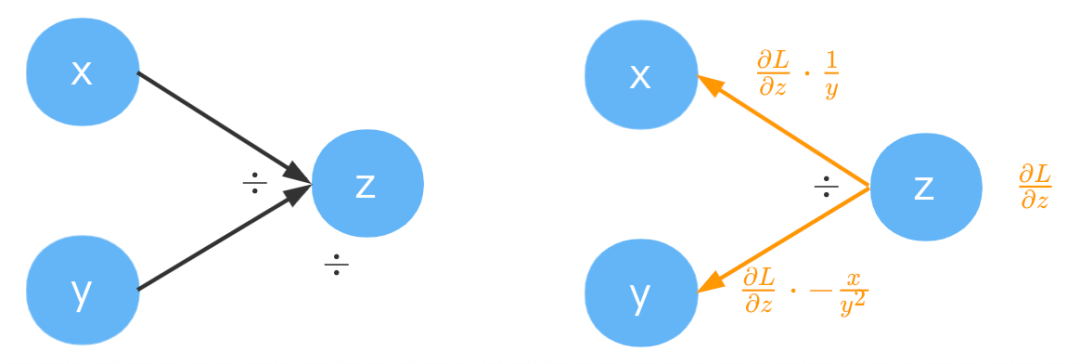
的梯度稍微有点复杂，。

我们现在看到的都是单变量，其实也可以是多变量(向量、张量或矩阵)。在多变量时，只需要独立计算向量中各个元素，即，向量的各个元素独立于其他元素进行对应元素的计算。在下文的矩阵乘法时会详细介绍。

分支

严格来说，分支并不是我们常见运算的一种。但是有些情况下很有用，比如进行广播操作时。

分支是最简单的复制形式，它的反向传播是上游传来的梯度之和。

Repeat

上面的分支操作有两个副本(或者分支)，也可以扩展为个副本，此时称为复制(Repeat)。

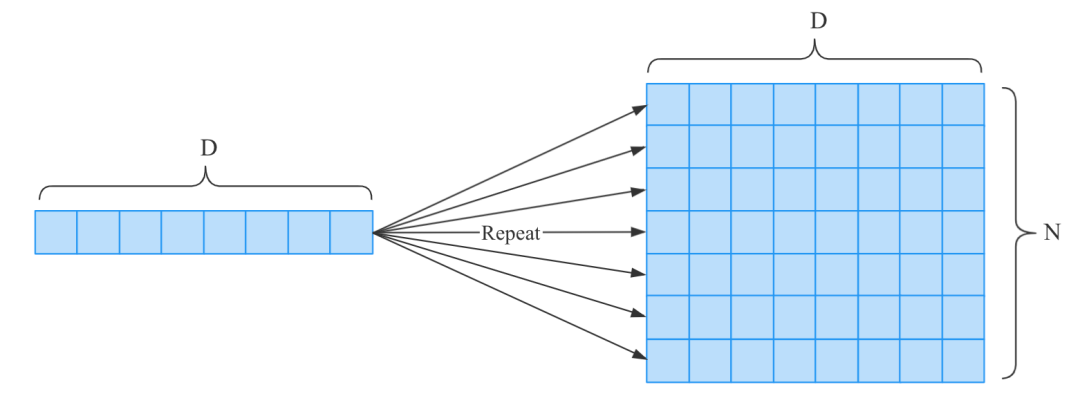
如上图，将长度为的数组复制了份，这个复制操作可以看成是个分支操作，所以它的反向传播可以通过个梯度的总和。

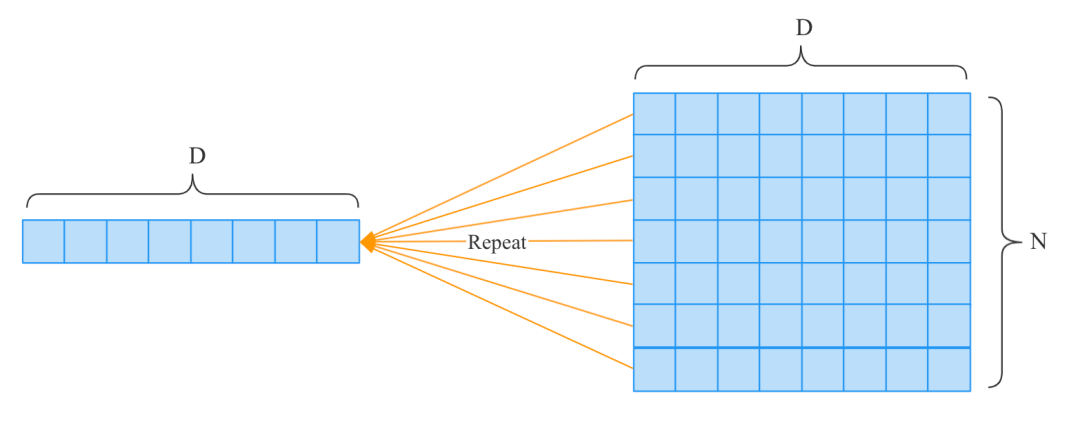
如果通过Numpy实现的化：

import numpy as np

D, N = 8, 7
x = np.random.randn(1,D)
y = np.repeat(x, N, axis=0) # axis=0 沿着行的方向复制N份，变成了(N,D)
# 上面是正向传播
# 下面是梯度
dy = np.random.randn(N,D) # y的梯度一定和y的维度保持一致
dx = np.sum(dy, axis=0, keepdims=True) # 同理，x的梯度也和x保持一致,这里变成了(1,D)

上图是简单介绍一下Numpy中axis的概念。当数组是1D的时候，只有一个轴，所以0轴的方向和2D的不同，要注意一下。

Numpy中的广播会复制数组的元素，可以通过这里的复制操作来表示。

Sum

Sum(求和)也是我们在深度学习中常用的运算。加法操作可以看成是求和的特殊形式。

考虑对一个对数组沿着第行的方向求和，此时正向传播和反向传播如下所示。

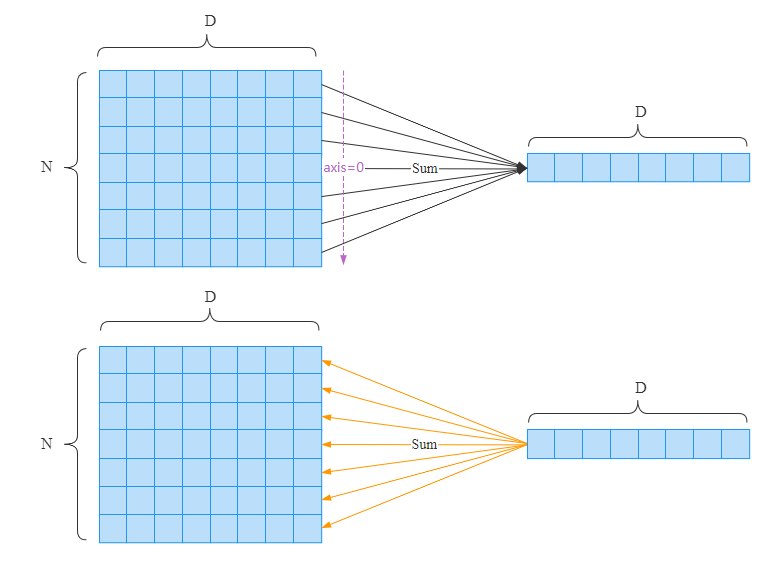
和加法一样，反向传播时将梯度(拷贝)分配到所有的箭头上，Sum操作是上面介绍的复制操作的逆向操作。即Sum的正向传播相当于复制操作的反向传播；Sum的反向传播相当于复制操作的正向传播。

我们也看一下通过Numpy实现的例子。

D, N = 8, 7
# 正向传播
x = np.random.randn(N, D)
y = np.sum(x, axis=0, keepdims=True) # 变成了(1,D)
# 反向传播
dy = np.random.randn(1, D) # 维度和y保持一致
dx = np.repeat(dy, N, axis=0) # 复制成了(N,D)

Matmul

Matmul是矩阵乘法(Matrix Multiply)，比如，考虑这个运算。的形状分别是、和。

它的反向传播稍微有点复杂。我们先来了解下雅可比矩阵(Jacobian matrix)。

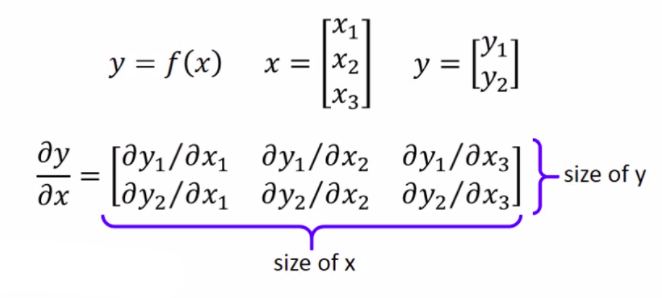
用每个对每个计算偏微分，计算得到的矩阵高度是的个数，宽度是的个数。

把展开得：

这里假设我们要计算对的导数。

我们先计算

接着计算对的导数，根据雅克比矩阵，有

看起来挺复杂，但是如果我们先把中第个元素的等式写出来，就会很简单，如：

所以 ，把完整的写出来，有

所以 ，这就解释了为什么计算矩阵乘法的反向传播时，有个参数需要转置的。

有

的形状是，的形状和它保持一致，也是。

的形状和一样，是

的形状是。

在推导上面的公式时，不要被写法的复杂所迷惑了，只要我们展开把等式写出来，或者用一个简单的比如的矩阵自己去推，就可以知道规律。

上面把写出来后，计算就很简单了，因为此时只与有关，对于剩下的元素的导数都是0，变成了。

下面介绍几个简单的一元操作。

Pow

计算，我们把看成是变量，看成是常数。只有一个变量，因此定义为一元操作。，一元操作比较简单，因此正向传播和反向传播画到一张图里面。

Log

取对数(Log)，一般指的是以指数为底。，那么。

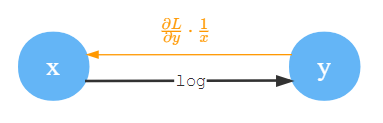
Exp

指数函数最简单了，，原样返回。

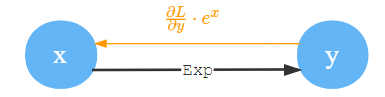
Neg

Neg是取负数的意思，，，可以理解为。