【数据竞赛】Kaggle竞赛如何保证线上线下一致性？

在数据集进行数据探索分析，做完样本的初步筛选，并对样本进行重新组织之后（如有必要）。接下来我们需要做的就是线下验证策略的设定。验证集设计的合理与否，对于整个竞赛都会带来非常大的影响，如果我们的模型线下验证结果和线上的结果不一致，将会导致无法继续进行后续的实验，就像是在摸奖一样，

• 注意：此处我们所说的不一致，指的是线下结果有一定幅度的提升，但线上却下降了的情况；如果线下提升幅度不是非常大，但是线上下降了可能是因为波动的原因，可以认为是合理的。

此外，一个鲁棒的验证策略，还可以帮助我们更好地调整我们模型的参数，验证各种框架以及特征的重要性等等。那么如何做好验证策略的设计呢？下面我们一共介绍三大类一共十一种常见的验证策略，并介绍这些对应策略常见的使用场景以及案例等。

1. 训练集验证集分割验证

1. 随机划分

1.1 简介

随机的训练集验证集切分是最为简单也是最为常见的验证策略。它的步骤也很简单：

1. 将训练集合按照一定比例随机切分为新的训练集和验证集；
2. 我们使用新的验证集进行训练并在验证集上进行验证；

它的示意图如下：

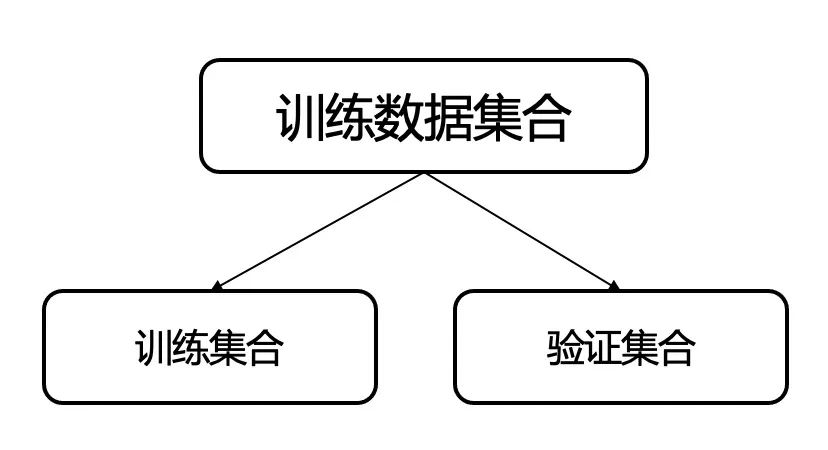
1.2 常见使用场景

简单的训练集和验证集划分策略目前经常会出现在一些数据集较大的问题同时时间因素影响不大的情况下，因为数据集较大的原因，验证一次的时间消耗较大，同时我们认为较大数据集的验证结果是相对可靠的，所以简单的训练集和验证集的划分就可以满足我们的需求。当然在早期一些小的数据集上有的朋友也会采用训练集验证集的划分策略，但是这个时候，我们需要将验证集的数据多划分一些，以保证验证结果相对置信。

• 如果我们的训练集合非常大，比如有上亿条记录，采用80：20的比例进行划分即可；当然70：30和90：10也都是可以的；
• 如果我们的训练集合一般，比如只有20000条数据，那么采用70：30左右的比例进行划分会较为合适点；尽可能往验证集上多划分一些数据，不过这个时候我们会更加倾向于使用接下来讲的K折交叉验证。

上面的比例只是一个参考，没有明确的计算公式说哪个比例会更好，需要大家自己实践来判断。

1.3 使用案例

# 将数据集划分为训练集和验证集合 
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
# 构建数据集
X, y = make_blobs(n_samples=100000)
# 数据集划分
val_ratio = 0.2
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=val_ratio)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape) 

(80000, 2) (20000, 2) (80000,) (20000,)

2. 分层划分

2.1 简介

分层划分主要常见于分类问题，有些分类问题的每个类标签的示例数并不均衡。分层划分的步骤和随机的类似，最好将数据集拆分为训练集和验证集，以便在每个类中保留与在原始数据集中观察到的差不多比例的样本。

1. 将训练集合按照一定比例分层划分为新的训练集和验证集；
2. 我们使用新的验证集进行训练并在验证集上进行验证；

2.2 常见使用场景

分层划分常见于类别标签不平衡的分类问题中，采用分层划分的策略，可以保证训练集和验证集合的样本的标签分布类似。

train_test_split(X, y, test_size=0.50, random_state=1, stratify=y) 

2.3 使用案例

# split imbalanced dataset into train and test sets without stratification
from collections import Counter
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
# 构建数据集
X, y = make_classification(n_samples=1000, weights=[0.95], flip_y=0, random_state=1)
print(Counter(y))
# 训练集验证集划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.50, random_state=1)
print('label distribution in train: ',Counter(y_train))
print('label distribution in test: ',Counter(y_test))  

Counter({0: 950, 1: 50})
label distribution in train:  Counter({0: 478, 1: 22})
label distribution in test:  Counter({0: 472, 1: 28})

# 训练集验证集分层划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.50, random_state=1, stratify=y)
print('label distribution in train: ',Counter(y_train)) 
print('label distribution in test: ',Counter(y_test)) 

Counter({0: 475, 1: 25})
Counter({0: 475, 1: 25})

2. K折交叉验证

1. 随机K折交叉验证

1.1 简介

简单的随机划分或者单次分层划分在我们数据集非常大，验证一次需要耗费较大量的计算代价和时间成本的时候较为常用。但是当我们的数据集并不是非常大时候，验证一次的成本也没有那么高的时候，为了保证模型的验证是靠谱的，大家最为常见的就是K折交叉验证。它的步骤如下：

1. 对数据集进行shuffle打乱顺序；
2. 将数据分成K折。K=5或10适用于大多数情况；
3. 保留一折用于验证，使用剩下的其它折数据进行模型的训练；
4. 在训练集合上训练模型，在验证集上评估模型，并记录该Fold的结果；
5. 现在对所有其它的Fold重复该过程，每次选择单折作为验证的数据集；
6. 对于每一次迭代，我们的模型都会在不同的数据集上进行训练和测试；
7. 最后我们将每一次的分数相加，采用最终的平均分作为我们的验证结果；

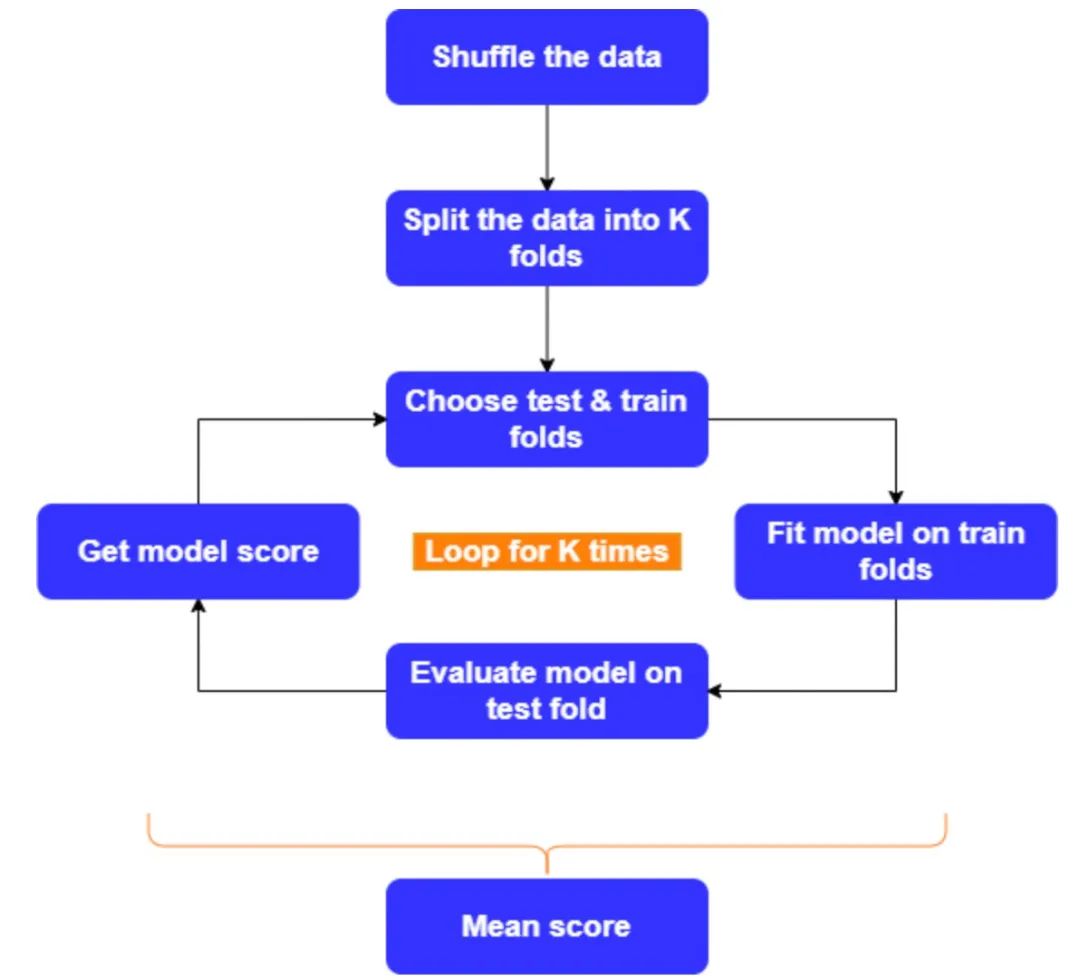
下面是一个五折交叉验证的可视化图例。

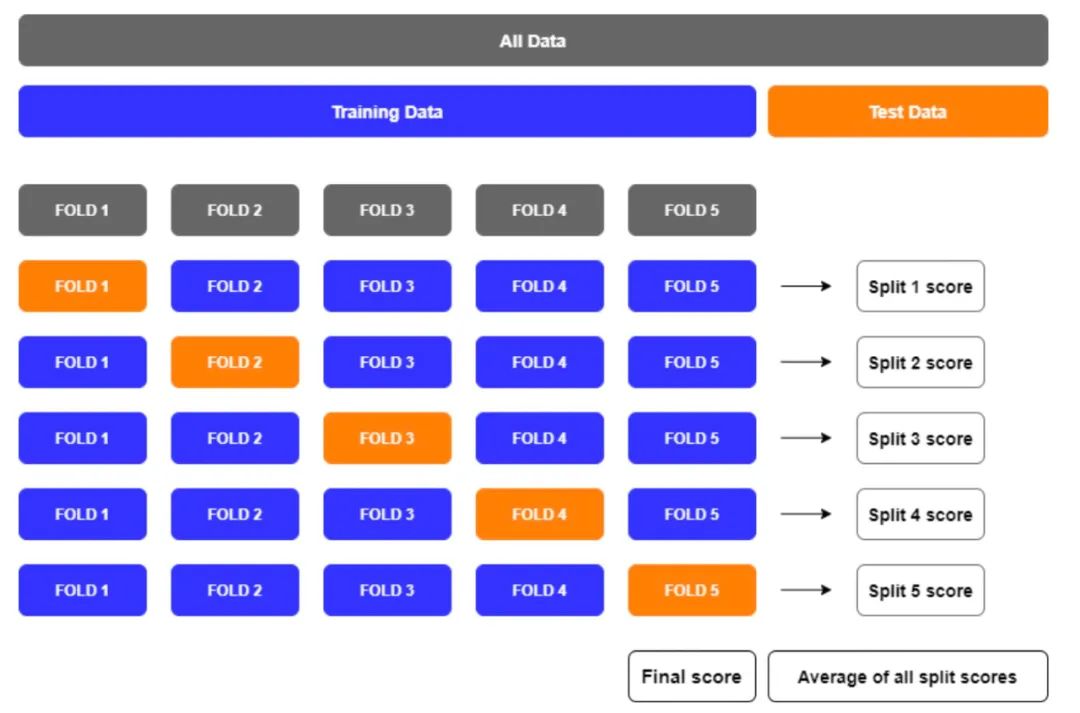
1.2 常见使用场景

K折交叉验证在很多的数据竞赛中都是非常常见的，当我们的数据量并不是非常大，验证一次的时间代价也相对较小，同时数据集受时间等影响也非常小的时候，我们就考虑采用K折交叉验证。从实践经验中，我们也发现：K折交叉验证不仅可以给我们带来一个更加靠谱的线下效果，与此同时，通过K折验证我们可以得到K个训练好的模型，采用K个模型分别对测试集进行预测并取均值或者中位数等作为最终预测结果带来的预测效果往往也会更好更稳定。

1.3 使用案例

import pandas as pd
import numpy as np
from sklearn.model_selection import KFold, cross_val_score  
# We will use this 'kf'(KFold splitting stratergy) object as input to cross_val_score() method

K = 5
kf =KFold(n_splits=K, shuffle=True, random_state=42) 
for train_index, test_index in kf.split(X, y):
    print(f'Fold:{cnt}, Train set: {len(train_index)}, Val set:{len(test_index)}')
    X_tr, X_val,y_tr,y_val = X[train_index],X[test_index], y[train_index],y[test_index]
    ...

2. 分层K折交叉验证

2.1 简介

简单的K折验证是最为常见的策略，但和随机划分处介绍的一样，我们希望我们每折中都可以有准确的数据分布。

• 在回归问题的情况下：我们选择折，使每折中的平均值大致相等；
• 在分类问题的情况下，每折被选择具有相同比例的分类标签。

分层K折叠在分类问题中更有用，在分类问题中，每折中具有相同百分比的标签非常重要。

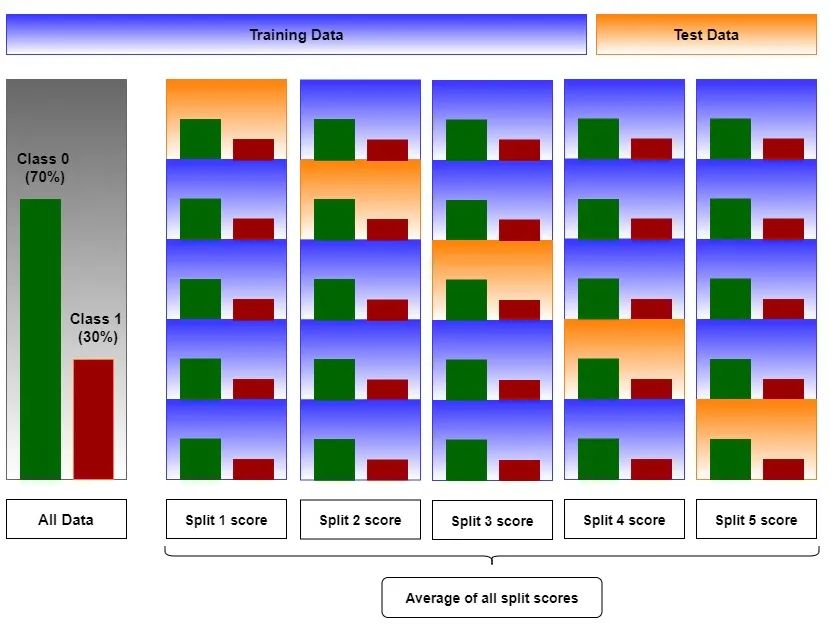
2.2 常见使用场景&案例

分层K折验证常见于类别标签不平衡的分类问题中，在有些情况也会出现在一些回归问题。使用案例和训练集验证集的分层划分是类似的，此处不再阐述。

3. 分组K折交叉验证

3.1 简介

随机K折交叉验证以及基于分层的K折验证已经适用于90%的时序影响较小的问题，但仍然存在一些问题。例如，如果我们的训练集和测试集是不同组的内容，此处组我们指的是需要预测的问题的主体，例如我们的问题是：

• 我们的训练集合是关于10万用户的历史逾期贷款记录（每个月产出一条记录）；我们需要预测另外1万个未出现在训练集合中的用户对应的记录是否会出现逾期贷款的问题。

此时我们的组就是用户的ID列表。再比如：

• 我们从多个病人身上收集医疗相关的数据，从每个病人身上采集了多个样本。我们的数据很可能取决于个别群体。在我们的案例中，每个样本对应的患者id就是它的组识识符。我们希望知道，基于这些收集到的数据训练得到的模型是否可以很好地推广到不可见的另外一个群体。为了衡量这一点，我们需要确保验证时每一折的所有样本都来是训练折中未出现的组。

此时我们的组就是患者的ID列表。关于分组K折验证的步骤可以分为：

1. 判定需要进行分组的ID；
2. 基于分组的ID进行随机K折验证；

3.2 常见使用场景

分组的K折交叉验证常常被用于判断基于某个特定组的数据训练得到的模型是否具有很好的泛化性，能够在未见过的组上取得很好的效果。

• 如果测试集和训练集合中的组存在较大的差异，这个时候对这些测试集数据采用分组训练预测往往能带来更加稳定的效果。
• 如果测试集和训练集合中的组存在的差异较小，简单的K折交叉验证即可。

3.3 使用案例

kf = GroupKFold(5)
grp_id = '' 
group = X[grp_id].copy()
for fold, (trn_idx, val_idx) in enumerate(kf.split(X, y, group)):
    print(f'Training fold {fold + 1}') 
    X_tr, X_val,y_tr,y_val = X[trn_idx],X[val_idx], y[trn_idx],y[val_idx]

4. 分层分组K折交叉验证

4.1 简介

从上面的介绍中，我们知道了分组和分层的使用场景。所以自然也就出现了分层分组的K折验证，典型的两个竞赛案例如下：

• PetFinder.my Adoption Prediction
• SIIM-ISIC Melanoma Classification

4.2 分层分组K折验证代码

分层分组的K折验证代码目前还未嵌入在sklearn工具包中，但是已经有很多朋友写过，下面摘取kaggle一个高赞的代码，供参考。

'''
    摘自：https://www.kaggle.com/jakubwasikowski/stratified-group-k-fold-cross-validation
'''

import random
import numpy as np
import pandas as pd
from collections import Counter, defaultdict
def stratified_group_k_fold(X, y, groups, k, seed=None):
    labels_num = np.max(y) + 1
    y_counts_per_group = defaultdict(lambda: np.zeros(labels_num))
    y_distr = Counter()
    for label, g in zip(y, groups):
        y_counts_per_group[g][label] += 1
        y_distr[label] += 1

    y_counts_per_fold = defaultdict(lambda: np.zeros(labels_num))
    groups_per_fold = defaultdict(set)

    def eval_y_counts_per_fold(y_counts, fold):
        y_counts_per_fold[fold] += y_counts
        std_per_label = []
        for label in range(labels_num):
            label_std = np.std([y_counts_per_fold[i][label] / y_distr[label] for i in range(k)])
            std_per_label.append(label_std)
        y_counts_per_fold[fold] -= y_counts
        return np.mean(std_per_label)
    
    groups_and_y_counts = list(y_counts_per_group.items())
    random.Random(seed).shuffle(groups_and_y_counts)

    for g, y_counts in sorted(groups_and_y_counts, key=lambda x: -np.std(x[1])):
        best_fold = None
        min_eval = None
        for i in range(k):
            fold_eval = eval_y_counts_per_fold(y_counts, i)
            if min_eval is None or fold_eval < min_eval:
                min_eval = fold_eval
                best_fold = i
        y_counts_per_fold[best_fold] += y_counts
        groups_per_fold[best_fold].add(g)

    all_groups = set(groups)
    for i in range(k):
        train_groups = all_groups - groups_per_fold[i]
        test_groups = groups_per_fold[i]

        train_indices = [i for i, g in enumerate(groups) if g in train_groups]
        test_indices = [i for i, g in enumerate(groups) if g in test_groups]

        yield train_indices, test_indices

5. Repeated K折交叉验证

5.1 简介

K折交叉验证将有限的训练数据集合划分为K个不重叠的折。K折中的每一折会被依次作为验证集，而所有其他折则会被合并作为新的训练数据集。在K个保持验证集上对K个模型进行了拟合和评估，同时将最终的均值作为我们的评估结果。这在实践中，其实我们大部分时候都是可以接受的，但也会发现下面的一个现象：

• 相同的特征，相同的K折验证，不同的随机种子，两次的验证结果分数相差的还挺多。

有些朋友会说K折交叉验证的结果是有较大噪音的，有的时候为了方便比较，我们往往会固定住随机种子，但是有的时候由于使用的机器和操作系统等的缘故，还会导致没法比较。那么如何缓解此类问题呢？最简单的：

• 那就再多做几次验证！

于是就有了Repeated K折交叉验证。它的步骤也非常简单：

• 设置重复的验证的次数M；
• 对于每一次验证，我们选用不同的随机种子进行K折验证；
• 将M次的验证结果取均值作为最终的验证结果。

注意：此处我们必须在同一数据集上执行K折交叉验证，在每次的每次重复中，同一个数据集被拆分为不同折。

该验证策略在《Applied Predictive Modeling》70页也有提到。

… repeated k-fold cross-validation replicates the procedure […] multiple times. For example, if 10-fold cross-validation was repeated five times, 50 different held-out sets would be used to estimate model efficacy.

5.2 常见使用场景

Repeated K折交叉验证可以很好地提升我们模型预估结果的置信度，一般常常使用在那些数据集相对不是非常大的情况下。因为这个时候，模型每次验证消耗的时间相对较短，计算资源的消耗也相对较小。和K折交叉验证类似，Repeated的K折交叉验证很容易并行化，其中每折或每个重复交叉验证过程可以在不同的内核或不同的机器上执行。

5.3 使用案例

• 案例1：5折验证重复5次。

repeats_time = 5
K            = 5 
cv = RepeatedKFold(n_splits=K, n_repeats=repeats_time, random_state=1) 

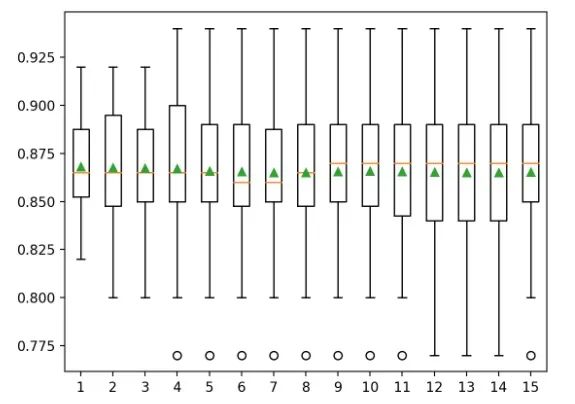
• 案例2：观测每次K折效果的波动情况

'''
    摘自：https://machinelearningmastery.com/repeated-k-fold-cross-validation-with-python/
'''
# compare the number of repeats for repeated k-fold cross-validation
from scipy.stats import sem
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import RepeatedKFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from matplotlib import pyplot

# evaluate a model with a given number of repeats
def evaluate_model(X, y, repeats):
    # prepare the cross-validation procedure
    cv = RepeatedKFold(n_splits=10, n_repeats=repeats, random_state=1)
    # create model
    model = LogisticRegression()
    # evaluate model
    scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
    return scores

# create dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1)
# configurations to test
repeats = range(1,16)
results = list()
for r in repeats:
    # evaluate using a given number of repeats
    scores = evaluate_model(X, y, r)
    # summarize
    print('>%d mean=%.4f se=%.3f' % (r, mean(scores), sem(scores)))
    # store
    results.append(scores)
# plot the results
pyplot.boxplot(results, labels=[str(r) for r in repeats], showmeans=True)
pyplot.show()

'''
>1 mean=0.8680 se=0.011
>2 mean=0.8675 se=0.008
>3 mean=0.8673 se=0.006
>4 mean=0.8670 se=0.006
>5 mean=0.8658 se=0.005
>6 mean=0.8655 se=0.004
>7 mean=0.8651 se=0.004
>8 mean=0.8651 se=0.004
>9 mean=0.8656 se=0.003
>10 mean=0.8658 se=0.003
>11 mean=0.8655 se=0.003
>12 mean=0.8654 se=0.003
>13 mean=0.8652 se=0.003
>14 mean=0.8651 se=0.003
>15 mean=0.8653 se=0.003 
'''

6. Nested K折交叉验证

6.1 简介

传统的K折交叉验证已经被广泛使用，大家在使用K折验证方案的时候经常会基于某一折进行调参，比如寻找最优的停止轮数，也就是说，我们每一折的验证结果都是在特定条件下相对最优的，但在实践问题中，我们不可能基于测试集得到最好的停止轮数的，这就会导致我们对模型效果的评估过于乐观。也就是说：

• K折交叉验证存在轻微的过拟合！

这在训练集和验证集随机划分的时候更加严重。那么我们该怎么做呢？Nested K折交叉验证就是用来缓解该问题的。

In order to overcome the bias in performance evaluation, model selection should be viewed as an integral part of the model fitting procedure, and should be conducted independently in each trial in order to prevent selection bias and because it reflects best practice in operational use.

Nested K折交叉验证将模型的超参调优作为模型的一部分，为了防止模型过拟合的问题，我们不再直接在验证的那一折上进行调参等操作，我们按照下面的步骤进行：

1. 基于特定的问题，我们将数据集进行特定的K折划分(随机/分层/分组...)，;
2. 在第L轮中，我们选用为验证集，其它折的数据集进行拼接得到我们新的训练集合；
3. 基于新的训练集合，我们采用折交叉进行超参数的调优，我们基于最优的参数重新训练得到我们的模型；
4. 使用重新训练得到的模型对我们的验证集进行预测，然后进行评估；

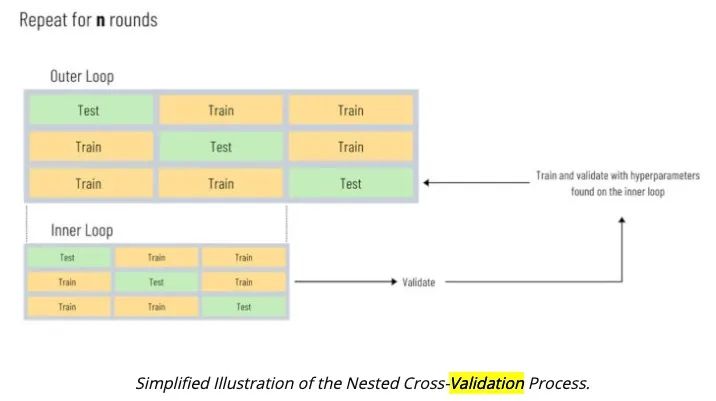
这么做，我们在整个流程中只在最后一次对其进行预测，所以得到的验证结果会更加靠谱。我们也可以这么去理解，

• 内部的交叉验证用来进行模型选择以及参数调优；
• 外部的交叉验证用来进行效果评估。

6.2 常见使用场景

适用于K折交叉验证的问题在Repeated K折交叉的问题中都是适用的。

6.3 使用案例

• 案例1：Nested K折交叉验证

'''
    该案例摘自：https://machinelearningmastery.com/nested-cross-validation-for-machine-learning-with-python/
''' 
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import KFold
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
# 构建训练集合
X, y = make_classification(n_samples=1000, n_features=20, random_state=1, n_informative=10, n_redundant=10)
# 1.外层K折交叉验证
cv_outer = KFold(n_splits=10, shuffle=True, random_state=1)

outer_results = list()
for train_ix, test_ix in cv_outer.split(X):
    # 第一层分割
    X_train, X_test = X[train_ix, :], X[test_ix, :]
    y_train, y_test = y[train_ix], y[test_ix]
    # 2. 内部交叉验证
    cv_inner = KFold(n_splits=3, shuffle=True, random_state=1) 
    model = RandomForestClassifier(random_state=1) 
    space = dict()
    space['n_estimators'] = [10, 100, 500]
    space['max_features'] = [2, 4, 6] 
    search = GridSearchCV(model, space, scoring='accuracy', cv=cv_inner, refit=True)
    result = search.fit(X_train, y_train)
    # 获取最好的模型
    best_model = result.best_estimator_ 
    yhat = best_model.predict(X_test)
    # 模型
    acc = accuracy_score(y_test, yhat)
    # store the result
    outer_results.append(acc)
    # report progress
    print('>acc=%.3f, est=%.3f, cfg=%s' % (acc, result.best_score_, result.best_params_))
# summarize the estimated performance of the model
print('Accuracy: %.3f (%.3f)' % (mean(outer_results), std(outer_results)))

• 案例2：使用现有的库

from nested_cv import NestedCV
from sklearn.ensemble import RandomForestRegressor

param_grid = {
     'max_depth': [3, None],
     'n_estimators': [10]
}

NCV = NestedCV(model=RandomForestRegressor(), params_grid=param_grid,
               outer_cv=5, inner_cv=5, n_jobs = -1,
               cv_options={'sqrt_of_score':True, 
                           'recursive_feature_elimination':True, 
                           'rfe_n_features':2})
NCV.fit(X=X,y=y)
NCV.outer_scores

3. 基于时间序列的验证

上面的所讲述的训练集验证集的划分策略以及K折交叉验证在时间影响较小的情况下是非常合适的，但是在很多时间影响较大的问题中，例如：

• 商家店铺销量预测；
• 用户视频观看时长预测问题；
• 网页流量预测；
• ...

这些问题如果直接使用传统的验证策略，往往会造成很严重的穿越问题，使得线下线上波动极大。因为时间序列相关的数据观测值之间的相关性紧靠时间的（自相关的）。但是，经典的交叉验证技术都是假设样本是独立同分布的，并且会导致时间序列数据上的训练和测试实例之间不合理的相关性（产生较差的泛化误差估计）。那么此类数据我们该如何做线下的验证呢？

1. 单折时间划分

1.1 简介

在时间相关的问题中，最常见的验证策略就是按照时间信息进行排序，然后选取某个时间点之后的数据集作为验证集合，前面的数据作为训练集合。

我们可以按照下面的策略进行：

1. 按照时间信息对我们的数据集进行排序；
2. 选取某个相对时间/绝对时间作为划分点，之前的作为训练结，之后的数据作为验证集合；

1.2 常见使用场景

当我们时间相关的数据量较大的时候，我们可以直接使用简单的按时间划分策略进行模型的验证。

1.3 使用案例

• 案例1：按照具体时间划分

df    = df.sort_values('time')
val_time = ''
df_tr = df.loc[df['time'] <= val_time] 
df_val= df.loc[df['time'] > val_time]

• 案例2：按照比例划分

df    = df.sort_values('time')
tr_ratio = 0.7
tr_size = df.shape[0] * tr_ratio 
df_tr = df.iloc[:tr_size] 
df_val= df.iloc[tr_size:]

2. 基于时间的N折验证

2.1 简介

上面简单的基于时间进行数据集划分的验证策略，在一些特殊的情况下，例如验证集中含有一段奇异值数据的时候，模型的波动会非常大，那么如何构建靠谱的线下验证策略呢？

• 使用Walk-Forward交叉验证策略或者是基于时间的N折交叉验证。

我们举个推荐相关的实际案例，在很多公司的推荐系统中，当模型优化到后期的时候，就会出现线上线下不一致的情况，那么如何缓解这种情况呢？或者至少降低这种情况发生的概率呢？首先我们看看大家是如何验证的......

• 90%公司的验证策略：选用T+1或者T+2的数据作为验证集，1,2,...,T的数据进行模型的训练；

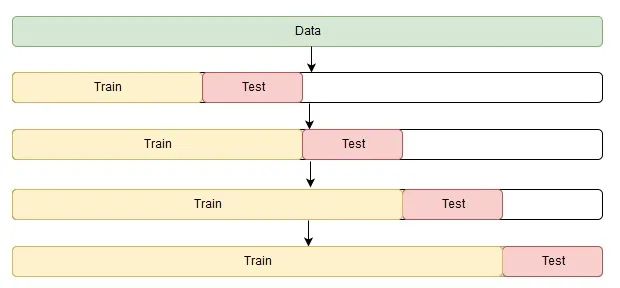
也就是最简单的时间划分策略，这么做就会有一个非常大的问题，因为很多公司会有很多的促销之类的活动，所以模型只选择一天进行验证就会出现不稳定的情况，但是在我们的实践中，发现，如果连续N天的验证都是有提升的，那么大概率该模型上线之后也能带来较为稳定的提升；其步骤也较为简单：

1. 选用T+1天的数据作为验证集，1,2,...,T的数据进行模型的训练；
2. 选用T天的数据作为验证集，1,2,...,T-1的数据进行模型的训练；
3. 选用T-1天的数据作为验证集，1,2,...,T-2的数据进行模型的训练；
4. 以此类推。

一般验证三天即可。

2.2 常见使用场景

适用于所有的中长时间序列建模的问题，即数据相对较多的情况。

2.3 使用案例

from sklearn.model_selection import TimeSeriesSplit
X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4],[1, 2], [3, 4], [1, 2], [3, 4]])
y = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])

for train_index, test_index in tscv.split(X):
    print("TRAIN:", train_index, "TEST:", test_index)
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]
    
'''
TRAIN: [0 1 2 3 4] TEST: [5]
TRAIN: [0 1 2 3 4 5] TEST: [6]
TRAIN: [0 1 2 3 4 5 6] TEST: [7]
TRAIN: [0 1 2 3 4 5 6 7] TEST: [8]
TRAIN: [0 1 2 3 4 5 6 7 8] TEST: [9]
'''

3. 时间序列的Nested CV

该思路很简单，为了得到模型更为靠谱的验证效果，会采用Nested的验证策略，对应的流程图如下：

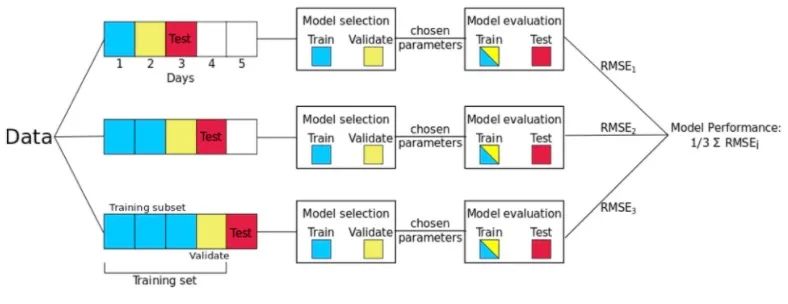
有兴趣的朋友可以进行深入的研究。

参考文献

1. Splitting a Dataset into Train and Test Sets
2. Train-Test Split for Evaluating Machine Learning Algorithms
3. Split Your Dataset With scikit-learn's train_test_split()
4. sklearn.model_selection.KFold
5. A Gentle Introduction to k-fold Cross-Validation
6. An Introduction to Statistical Learning
7. Repeated k-Fold Cross-Validation for Model Evaluation in Python
8. Nested Cross-Validation for Machine Learning with Python
9. Tutorial: K Fold Cross Validation
10. Stratified Group k-Fold Cross-Validation
11. Introduction to GroupKFold
12. SIIM Stratified GroupKFold 5-folds
13. Simple LGBM GroupKFold CV
14. Stratified Group k-Fold
15. Learn ML from Sklearn: Cross Validation
16. Applied Predictive Modeling
17. sklearn.model_selection.RepeatedKFold
18. Key Machine Learning Technique: Nested Cross-Validation, Why and How, with Python code
19. Nested-Cross-Validation
20. On Over-fitting in Model Selection and Subsequent Selection Bias in Performance Evaluation, 2010.
21. Tutorial: Time Series Analysis and Forecasting
22. Time Series Cross Validation
23. Correct time-aware cross-validation scheme
24. Nested cross validation for model selection
25. Cross validation on time series data
26. Train/Test Split and Cross Validation – A Python Tutorial