宁波市2022学年第一学期选考模拟卷第16题解析-轻识

说在前面

新教材怎么教，取决于新高考怎么考。新高考的题目类型如何分布？题目难度如何？一直是老师们最为关心的问题。

在仅有课标和教材，没有考纲和样卷的情况下，各类名校和联盟的命题老师们认真思考、努力探索，为大家提供了多份质量上乘、极具参考价值的联考模拟卷。

认真研究这些模拟卷，分析它们的命题思路和解题方法，总结题型和算法框架，不仅有利于高考备考，对新课教学也有很大的借鉴意义。

宁波市2022学年第一学期选考模拟卷第16题

一

题目

16. 魔术师预先将一副牌中的13张黑桃（A为1，J为11，Q为12，K为13）排好后叠在一起，牌面朝下。他将最上面的那张牌翻过来，正好是黑桃A。将黑桃A放在桌子上，然后按顺序从上到下数手上的余牌：第二次数1、2，将数到的第一张牌放在这叠牌的下面，将第二张牌翻过来，正好是黑桃2，将它放在桌子上；第三次数1、2、3，将前面两张依次放在这叠牌的下面，再翻第三张牌，正好是黑桃3，放在桌子上。这样依次进行，将13张牌全翻出来，最后桌子上牌的顺序是A、2、...... K。问魔术师手中的牌原始顺序是怎样的？

小王和小李对问题进行了分析与算法设计，写了Python函数way()正确解答了问题，请回答下列问题。

（1）原来牌的顺序中，黑桃3放在自上向下第（填阿拉伯数字）个位置。

（2）请在划线处填入合适的代码。

def way():

a = [i for i in range(1, 14)]

b =[0]*13 # 0代表牌面未定

head = 0; tail = 0

for i in range(1, 14):

cnt = 1

while cnt < i:

a[tail] = ①

head = (head + 1) % 13

tail = (tail + 1) % 13

②

③

head = (head + 1) % 13

return b

print(way())

二

考查知识点

模拟算法、一维数组和队列基本操作，要求学生理解使用循环队列模拟数牌过程的算法，掌握一维数组和队列基本操作，深切理解数组下标从0开始。

三

解析

题目考查循环队列基本操作。循环队列与队列的区别在于队头指针和队尾指针加1以后要对13求余数，以实现循环出入队列的功能。

我们依次把牌面值添加到数组b中，可以发现第一轮（红色字体）分别翻出牌面值为1、2、3、4的牌，它们所处位置分别是第1、3、6、10张牌，故第（1）题答案为6。

翻牌问题其实是约瑟夫环问题的一个变形，每张牌的位置就相当于每个人所站的位置，牌可以被拿走，但位置编号（取值范围1-13）一开始就确定了，并存储在数组a中，将元素值减1，则恰好对应其下标。程序使用数组b存储牌面的原始顺序，故我们可以用b[a[i]-1]表示位置a[i]处的牌面，这是第③空的算法依据。

设置变量i作为牌的编号（牌面值），外层循环让i从1开始依次递增。循环体内模拟数数过程，cnt为计数器，while循环重复（i-1）次，通过出队和入队操作，把上方的（i-1）张牌转移到下方，故第①空答案为a[head]，第②空答案为cnt += 1。

第③空的作用是从循环队列中取出队头元素a[head]，此时翻出的牌面值为i，其在数组b中的下标恰好为（a[head]-1），故第③空答案为b[a[head]-1] = i。

本题程序使用循环队列模拟数牌过程，把每张牌的位置存储在队列a中。通过出队和入队操作，把上方的牌转移到下方；被翻出的牌则只出队不入队，并设置翻牌处的牌面值为i。算法逻辑清晰，代码实现简明，问题难度适中，是一道经典的好题。

四

答案

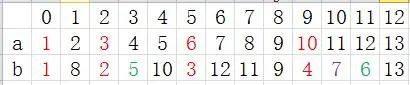
（1）6

（2）① a[head]

② cnt += 1

③ b[a[head]-1] = cnt 或 b[a[head]-1] = i

五

拓展思考

题目程序使用队列a存储了每张牌的位置（取值范围1-13），需要将元素值减1后才能对应数组b的下标，稍微绕了一点弯路；我们可以直接在队列a中存储数组b的下标。

此外，题目程序默认总共有13张牌，数据量稍微有些大；我们可以将程序推广到n张牌的情形。例如当n=4时，牌的编号依次为1,4,2,3。

翻牌问题其实是约瑟夫环问题的一个变形，它将原问题的固定报数上限改成从1到n逐次递增，返回被翻牌的位置编号，并为该位置设置牌面值。解决约瑟夫环问题（翻牌问题）的方法很多，常用一维数组、循环单链表或循环队列来存储位置编号。

可以把题目修改如下：已知有n张牌依次编号为1-n，洗牌后叠在一起，牌面朝下。现在按规则翻牌，翻开第1张牌，牌面恰好为1，将它放在桌子上；第二次边拿牌边数数，将数到的第一张牌放在这叠牌的下面，将第二张牌翻过来，牌面恰好为2，将它放在桌子上；第三次数1、2、3，将前面两张依次放在这叠牌的下面，再翻第三张牌，牌面恰好为3，放在桌子上。以此规则继续翻牌，直至将n张牌全翻出来，依次翻出牌的顺序是1、2、...... n。

请问原来n张牌从上到下牌面值依次为多少？

参考样例：当n=4时，牌面值依次为1,4,2,3；当n=5时，牌面值依次为1,3,2,5,4。

（1）当n=6时，牌面值依次为。

（2）下面分别使用自定义函数way_1()，way_2()，way_3()实现设置牌面值功能，请将缺失的代码补充完整：

def way_1(n):

a = [i for i in range(n)]

b = [0] * n # 0代表牌面未定

i = 0

for m in range(1,n+1):

cnt = 1

while ① : # 依次将m-1张牌放到牌堆底部

if a[i] >= 0:

cnt += 1

i = (i + 1) % n

while a[i] == -1: # 跳过已删除元素

i = ②

③ # 设置a[i]处的牌面为m

a[i] = -1 # 标记a[i]被删除

return b

def way_2(n):

a = [[i, i+1] for i in range(n)]

a[n-1][1] = 0 # 构造循环单链表

b = [0] * n # 0代表牌面未定

pre = n - 1 # 指向头节点的前驱节点

for m in range(1,n+1):

for j in range(m-1): # 依次将m-1张牌放到牌堆底部

pre = ④

p = a[pre][1] # 指向翻牌位置

⑤ # 设置翻牌位置的牌面为m

a[pre][1] = ⑥ # 删除a[p]

return b

def way_3(n):

a = [i for i in range(n)]

b = [0] * n # 0代表牌面未定

head = tail = 0

for i in range(1,n+1):

for j in range(i-1): # 依次将i-1张牌放到牌堆底部

a[tail] = ⑦

head = (head + 1) % n

tail = ⑧

⑨

head = (head + 1) % n

return b

# 主函数部分

n = 6

print(way_1(n))

print(way_2(n))

print(way_3(n))

六

拓展思考答案

（1）1, 4, 2, 5, 6, 3

（2）① cnt < m

② (i + 1) % n

③ b[a[i]] = m

④ a[pre][1]

⑤ b[a[p][0]] = m

⑥ a[p][1]或a[a[pre][1]][1]

⑦ a[head]

⑧ (tail + 1) % n

⑨ b[a[head]] = i

写在后面

为了保证解析的原创性和思维的独特性，我都是独立解题后，先不看答案(除非题目不会做)，直接把解析写好，再去看答案。

当然，如果发现参考答案有更好的思路，我还是很乐于学习和借鉴的。同时，由于本人水平有限，解析中难免出现疏漏甚至错误之处，敬请谅解。

无论是赞同还是反对我的看法，都请你给我留言。如果你有新的想法，千万不要憋在心里，请发出来大家一起讨论。让我们相互学习，共同进步！

需要本文word文档、源代码和课后思考答案的，可以加入“Python算法之旅”知识星球参与讨论和下载文件，“Python算法之旅”知识星球汇集了数量众多的同好，更多有趣的话题在这里讨论，更多有用的资料在这里分享。

我们专注Python算法，感兴趣就一起来！

相关优秀文章：

阅读代码和写更好的代码

最有效的学习方式

Python算法之旅文章分类