【统计学习方法】 第3章 k近邻法(三)
共 4181字,需浏览 9分钟
·
2021-02-15 22:48
点击上方“公众号”可订阅哦!
在scikit-learn 中,与近邻法这一大类相关的类库都在sklearn.neighbors包之中。KNN分类树的类是KNeighborsClassifier,KNN回归树的类是KNeighborsRegressor。
以下主要介绍下函数的参数注解和使用Iris数据集实现k近邻分类
1
●
函数参数注解
neighbors.KNeighborsClassifier(n_neighbors=5,weights='uniform',algorithm='auto',leaf_size=30,p=2,metric='minkowski',metric_params=None,n_jobs=None,**kwargs,)
参数注释:
n_neighbors:K值的选择与样本分布有关,一般选择一个较小的K值,可以通过交叉验证来选择一个比较优的K值,默认值是5。如果数据是三维一下的,如果数据是三维或者三维以下的,可以通过可视化观察来调参。
weight:临近实例的权重,可以取三个值,‘uniform’为权重相同的情况,‘distance’表示权重与距离成反比,也可以自己定义函数来对权值进行设定。
algorithm:可以取四个值:{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’},‘ball_tree‘、’kd_tree’表示使用‘ball_tree'和'kd_tree'进行计算,’brute‘表示使用brute-force搜索,’auto‘表示计算时尝试选择最合适的算法进行计算。
leaf_size: 选择’ball_tree'和‘kd_tree'时树的叶子数量,默认为30。
p:即距离度量的p值,默认为2即欧氏距离。
metric:距离度量方法的选择
n_jobs:为邻居搜索运行的并行作业数。默认为1,-1表示使用所有处理器。
属性:
classes_:分类器已知的类标签
effective_metric_:使用的距离度量。它将与度量参数相同或与其相同,例如 如果metric参数设置为“ minkowski”,而p参数设置为2,则为“ euclidean”。
n_samples_fit_:拟合数据中的样本数。
方法:
fit(X, y):从训练数据集中拟合k最近邻分类器。
kneighbors([X, n_neighbors, return_distance]):查找点的K邻居。
predict(X):预测提供的数据的类标签。
2
●
knn实例
数据集:
Iris数据集是常用的分类实验数据集,由Fisher, 1936收集整理。Iris也称鸢尾花卉数据集,是一类多重变量分析的数据集。数据集包含150个数据集,分为3类,每类50个数据,每个数据包含4个属性。iris以鸢尾花的特征作为数据来源,常用在分类操作中。该数据集由3种不同类型的鸢尾花的50个样本数据构成。其中的一个种类与另外两个种类是线性可分离的,后两个种类是非线性可分离的。

在此实例中我们使用前面两个维度的数据

代码:
import numpy as npimport matplotlib.pyplot as pltfrom matplotlib.colors import ListedColormapfrom sklearn import neighbors, datasets%matplotlib inlinen_neighbors = 15 #设置K值:15个邻居iris = datasets.load_iris() #加载数据# 我们加载数据的前面两个维度作为特征数据X = iris.data[:, :2]y = iris.targeth = .01 # 画网格的步长,数值越小网格越细腻for weights in ['uniform', 'distance']:# 创建分类器,并拟合数据clf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights)clf.fit(X, y)# 绘制训练集的边界# 网格范围 [x_min, x_max]x[y_min, y_max].x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1# 生成随机数据来做测试集,然后作预测xx, yy = np.meshgrid(np.arange(x_min, x_max, h),np.arange(y_min, y_max, h))# 连接xx,yy。.ravel扁平化Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])# 将结果放入颜色Z = Z.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, Z)# 绘制训练点plt.scatter(X[:, 0], X[:, 1], c=y,edgecolor='k', s=20)plt.xlim(xx.min(), xx.max())plt.ylim(yy.min(), yy.max())plt.title("3-Class classification (k = %i, weights = '%s')"% (n_neighbors, weights))plt.show()
以下是得到的效果图:

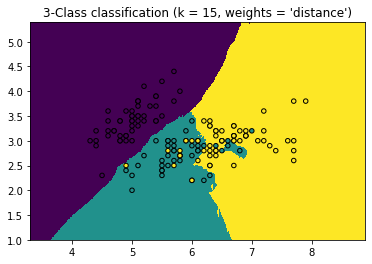
参考来源:
https://blog.csdn.net/weixin_44980490/article/details/105958744?ops_request_misc=%25257B%252522request%25255Fid%252522%25253A%252522161320906816780255290029%252522%25252C%252522scm%252522%25253A%25252220140713.130102334.pc%25255Fall.%252522%25257D&request_id=161320906816780255290029&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_v2~rank_v29-15-105958744.pc_search_result_cache&utm_term=iris%25E6%2595%25B0%25E6%258D%25AE%25E9%259B%2586%25E5%258F%25AF%25E8%25A7%2586%25E5%258C%2596
https://blog.csdn.net/Albert201605/article/details/82313139?ops_request_misc=%25257B%252522request%25255Fid%252522%25253A%252522161320758616780264041015%252522%25252C%252522scm%252522%25253A%25252220140713.130102334.pc%25255Fall.%252522%25257D&request_id=161320758616780264041015&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_v2~rank_v29-9-82313139.pc_search_result_cache&utm_term=iris%25E6%2595%25B0%25E6%258D%25AE%25E9%259B%2586
https://scikit-learn.org/stable/auto_examples/neighbors/plot_classification.html#sphx-glr-auto-examples-neighbors-plot-classification-py
https://blog.csdn.net/jiang425776024/article/details/87122387?ops_request_misc=%25257B%252522request%25255Fid%252522%25253A%252522161326694916780261939912%252522%25252C%252522scm%252522%25253A%25252220140713.130102334.pc%25255Fall.%252522%25257D&request_id=161326694916780261939912&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_v2~rank_v29-2-87122387.pc_search_result_cache&utm_term=ListedColormap
END

深度学习入门笔记
微信号:sdxx_rmbj
日常更新学习笔记、论文简述
