人脸识别最新进展

旷视的一篇文章人脸识别中Softmax-based Loss的演化史对于人脸识别的前期发展做了充分的总结，本文旨在总结一下人脸识别后期研究。

Mis-classifified Vector Guided Softmax Loss for Face Recognition

现有人脸识别算法存在的问题

论文创新点

MV-Softmax loss的设计理念和损失函数

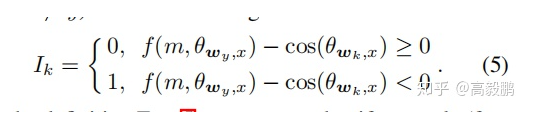
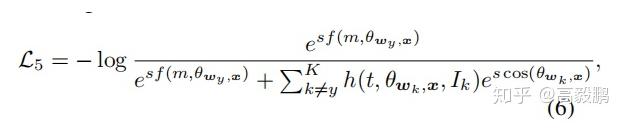
学习这个损失，并分析一下其中的设计理念。作者认为良好分离的特征向量对学习问题的影响很小。这就意味着错误分类的特征向量对于提高特征的鉴别能力变得尤为关键。为了将训练重点放在真正具有鉴别特性的难例样本上(即错误分类向量)。作者定义了一个二值指标Ik，自适应地表示当前阶段某个样本(特征)是否被特定分类器wk(其中k不等于其真正的类y)误分类，具体形式如式5所示。从Eq.(5)的定义可以看出，如果一个样本(特征)分类错误，即， f(m, Θwy, x) - cos(Θwk, x) < 0(例如:，在图1的左子图中，特征x2属于类1，但分类器w2对其进行了错误分类，即f(m，Θw1, x2) - cos(Θw2, x2) < 0)，该样本x2将会被暂时强调，即标Ik= 1。这样，困难的例子就被明确的指出来，我们主要针对这些困难的例子进行区分训练。换句话说作者认为落在间隔的样本为难例样本。因此作者定义了新的损失函数，如公式6所示。

公式6中的h(t，Θwk,x, Ik)≥1是一个重置权重函数，以强调指明的错误分类向量。这里我们给出了两个候选，一个是所有错误分类的类的固定权重如公式7和一个自适应的权重如公式8。

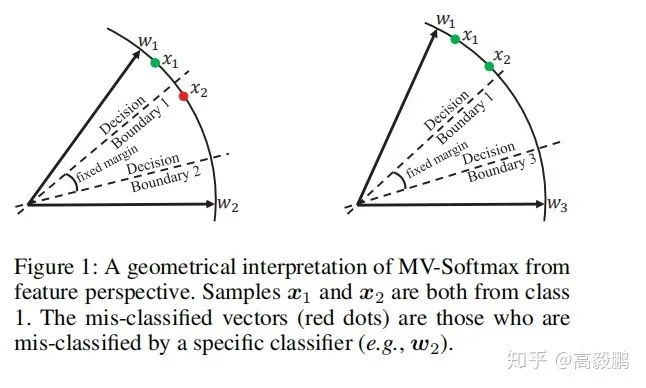
难例挖掘分析

如fig1所示，假设我们有两个样本(特征)x1和x2，它们都来自类1，其中x1是分类良好的，而x2不是。HM-Softmax经验地表示了困难样本，抛弃了简单样本x1，使用困难样本x2进行训练。F-Softmax没有明确表示困难样本，但它重新加权所有的样本，使较困难的一个x2有相对较大的损失值。这两种策略都是直接从损失的角度出发的，难例的选择没有语义指导。而MV-Softmax损失却不同。

自适应间隔分析

假设我们有来自类1的样本x2，且其没有正确分类（如图1左图的红点）。原始的softmax loss旨在让

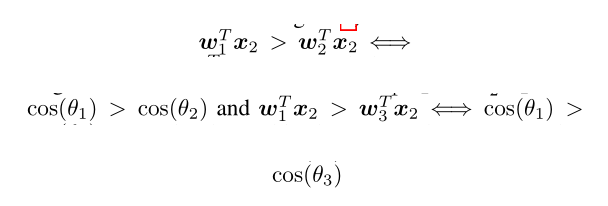
为了让该目标函数更严格，基于间隔的损失函数介绍了一个来自ground truth类（即Θ1）角度的边界函数

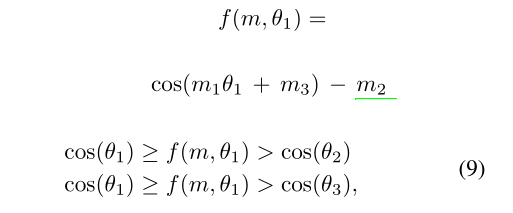
其中，f(m, Θ1)对于不同的类具有相同且固定的边界，忽略了与其他非ground truth类(如:Θ2和Θ3)的潜在区别性。为了解决这些问题，我们的MV-Softmax loss试图从其他非ground truth类的角度进一步扩大特征。具体来说，我们为错误分类的特征x2引入了一个边界函数h∗(t，Θ2):

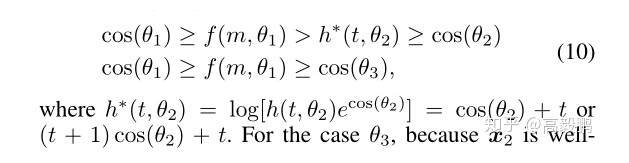
对于Θ3，因为x2被其正确分类（即判定x2不是类3），所以我们不需要对其添加额外的增强去进一步增大其的边界。而且，我们的MV-Softmax loss也为不同的类设置了不同的可适应边界。以 MV-AM-Softmax（即

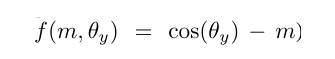
）为例，对于错误分类的类，其边界为

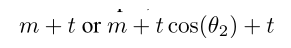
。然而对于正确分类的类，其边界为m。基于这些特性，我们的MV-Softmax loss解决了基于间隔损失函数的第二和第三个缺点。

class SVXSoftmax(nn.Module):
    r"""Implement of Mis-classified Vector Guided Softmax Loss for Face Recognition
        (https://arxiv.org/pdf/1912.00833.pdf):
        Args:
            in_features: size of each input sample
            out_features: size of each output sample
            device_id: the ID of GPU where the model will be trained by model parallel.
                       if device_id=None, it will be trained on CPU without model parallel.
            s: norm of input feature
            m: margin
            cos(theta+m)
        """
    def __init__(self, in_features, out_features, xtype='MV-AM', s=32.0, m=0.35, t=0.2, easy_margin=False):
        super(SVXSoftmax, self).__init__()
        self.xtype = xtype
        self.in_features = in_features
        self.out_features = out_features

        self.s = s
        self.m = m
        self.t = t

        self.weight = Parameter(torch.FloatTensor(out_features, in_features))
        self.weight.data.uniform_(-1, 1).renorm_(2, 1, 1e-5).mul_(1e5)
      
        self.easy_margin = easy_margin
        self.cos_m = math.cos(m)
        self.sin_m = math.sin(m)
        
    def forward(self, input, label):
        cos_theta = F.linear(F.normalize(input), F.normalize(self.weight))
        cos_theta = cos_theta.clamp(-1, 1)  # for numerical stability
        batch_size = label.size(0)
        gt = cos_theta[torch.arange(0, batch_size), label].view(-1, 1)  # ground truth score
        if self.xtype == 'MV-AM':
            mask = cos_theta > gt - self.m
            hard_vector = cos_theta[mask]
            cos_theta[mask] = (self.t + 1.0) * hard_vector + self.t  # adaptive
            # cos_theta[mask] = hard_vector + self.t  #fixed
            if self.easy_margin:
                final_gt = torch.where(gt > 0, gt - self.m, gt)
            else:
                final_gt = gt - self.m
        elif self.xtype == 'MV-Arc':
            sin_theta = torch.sqrt(1.0 - torch.pow(gt, 2))
            cos_theta_m = gt * self.cos_m - sin_theta * self.sin_m  # cos(gt + margin)

            mask = cos_theta > cos_theta_m
            hard_vector = cos_theta[mask]
            cos_theta[mask] = (self.t + 1.0) * hard_vector + self.t  # adaptive
            # cos_theta[mask] = hard_vector + self.t #fixed
            if self.easy_margin:
                final_gt = torch.where(gt > 0, cos_theta_m, gt)
            else:
                final_gt = cos_theta_m
                # final_gt = torch.where(gt > cos_theta_m, cos_theta_m, gt)
        else:
            raise Exception('unknown xtype!')
        cos_theta.scatter_(1, label.data.view(-1, 1), final_gt)
        cos_theta *= self.s
        return cos_theta

CurricularFace

人脸识别中常用损失函数主要包括两类，基于间隔和难样本挖掘，这两种方法损失函数的训练策略都存在缺陷。

为了解决上述问题，优图实验室引入了Curriculum Learning的概念来优化损失函数。

Curriculum Learning即课程学习

CurricularFace的算法思想

将课程学习的思想嵌入到损失函数中，以实现一种新的深度人脸识别训练策略。该策略主要针对早期训练阶段的易样本和后期训练阶段的难样本，使其在不同的训练阶段，通过一个课程表自适应地调整简单和困难样本的相对重要性。也就是说，在每个阶段，不同的样本根据其相应的困难程度被赋予不同的重要性。

CurricularFace和传统课程学习的异同

CurricularFace的设计理念及损失函数

为了在整个训练过程中实现自适应课程学习的目标，优图实验室设计了一种新的系数函数，该函数包括以下两个因子：

损失函数

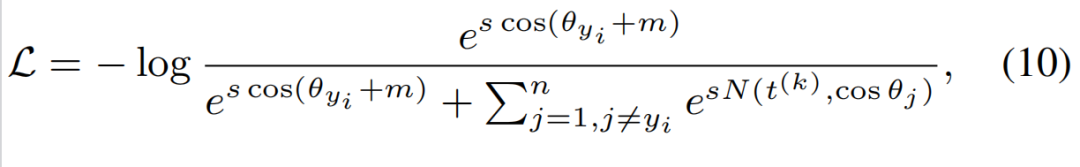
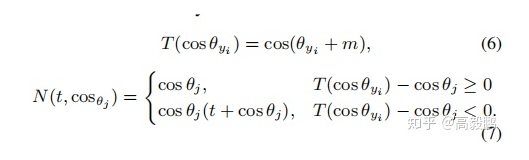
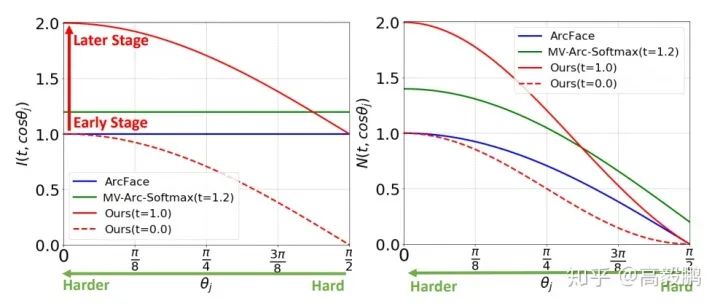
上式的含义是：如果一个样本是易样本，它的Negative余弦相似度保持原始状态，即为；如果一个样本是难样本，它的Negative余弦相似度就变成了。

我们再来看下公式中的自适应估计参数_t_是如何定义的。优图实验室采用指数移动平均（EMA）来实现这个自适应的参数。公式如下，其中的是第k个Batch的Positive余弦相似度均值，是冲量参数设为0.99。

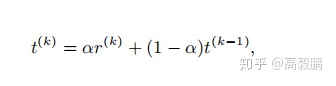
class CurricularFace(nn.Module):
    r"""Implement of CurricularFace (https://arxiv.org/pdf/2004.00288.pdf):
    Args:
        in_features: size of each input sample
        out_features: size of each output sample
        device_id: the ID of GPU where the model will be trained by model parallel.
                       if device_id=None, it will be trained on CPU without model parallel.
        m: margin
        s: scale of outputs
    """
    def __init__(self, in_features, out_features, m = 0.5, s = 64.):
        super(CurricularFace, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.m = m
        self.s = s
        self.cos_m = math.cos(m)
        self.sin_m = math.sin(m)
        self.threshold = math.cos(math.pi - m)
        self.mm = math.sin(math.pi - m) * m
        self.kernel = Parameter(torch.Tensor(in_features, out_features))
        self.register_buffer('t', torch.zeros(1))
        nn.init.normal_(self.kernel, std=0.01)

    def forward(self, embbedings, label):
        embbedings = l2_norm(embbedings, axis = 1)
        kernel_norm = l2_norm(self.kernel, axis = 0)
        cos_theta = torch.mm(embbedings, kernel_norm)
        cos_theta = cos_theta.clamp(-1, 1)  # for numerical stability
        with torch.no_grad():
            origin_cos = cos_theta.clone()
        target_logit = cos_theta[torch.arange(0, embbedings.size(0)), label].view(-1, 1)

        sin_theta = torch.sqrt(1.0 - torch.pow(target_logit, 2))
        cos_theta_m = target_logit * self.cos_m - sin_theta * self.sin_m #cos(target+margin)
        mask = cos_theta > cos_theta_m
        final_target_logit = torch.where(target_logit > self.threshold, cos_theta_m, target_logit - self.mm)

        hard_example = cos_theta[mask]
        with torch.no_grad():
            self.t = target_logit.mean() * 0.01 + (1 - 0.01) * self.t
        cos_theta[mask] = hard_example * (self.t + hard_example)
        cos_theta.scatter_(1, label.view(-1, 1).long(), final_target_logit)
        output = cos_theta * self.s
        return output

Circle Loss

详情参见：

https://zhuanlan.zhihu.com/p/117716663

AM-LFS：AutoML for Loss Function Search

论文创新点

回顾之前的损失函数

• softmax

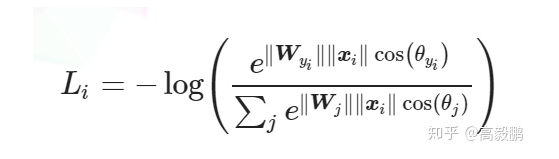
• Margin-based Softmax Loss

和 之间能够插入一个可微变换函数t(⋅)t(⋅)来调节角度，进而得到margin可变的softmax loss：

不同的t(⋅)t(⋅)可以得到不同的损失函数，原文中总结了如下几种：

• Focal Loss

除了在概率上做变化外，Focal Loss对softmax loss做了如下变化：

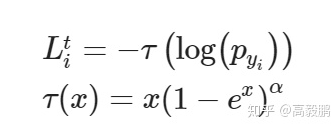
Loss函数分析

• Focal Loss

Focal loss的提出主要是为了解决imbalanced的问题。相对于原始的softmax loss，focal loss在求导之后等于原始的softmax loss求导结果再乘以 ，换言之 用来缓解imbalance的问题。

• Margin-based Softmax Loss

为方便说明，我们可以假设所有的矢量是单位矢量，即 和

我们使用公式(4)中的损失函数来分别对 （类内，intra-class）和 （类间，inter-class）求导，得到：

文中进一步将类内距离与类间距离的相对重要性定义为 和 的梯度范数相对于margin-based softmax loss的比率

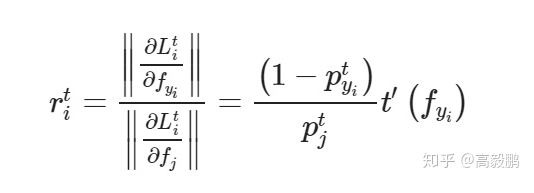
同理相对于原始的softmax loss（公式1）的重要性比率是：

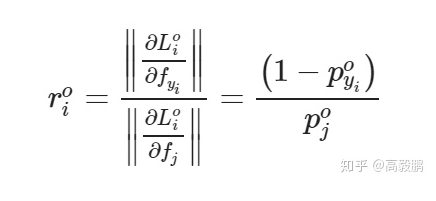
进一步可以求得：

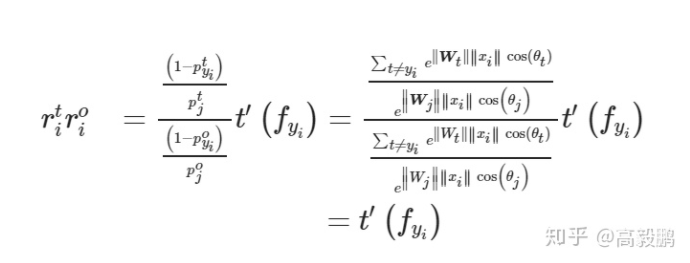
t(⋅)的导函数实际上是具有控制类内距离对于类间距离显著性的作用，这也是用数学推导的方式证明了间隔的重要性。

搜索空间

由前面的损失函数分析我们对softmax做如下变换，得到新的损失函数如下，

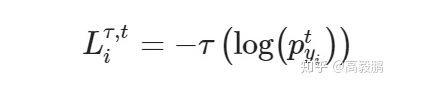
其中

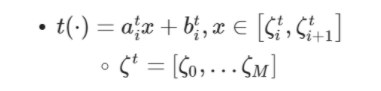
M表示间隔数，即

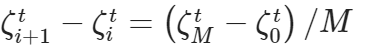
所以t(⋅)函数由三个超参数组成 , 和 组成。

ττ同理由三个超参数组成： , 和 组成。

因此搜索空间为，

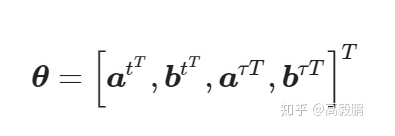
参数优化

双层（Bilevel）优化定义如下：

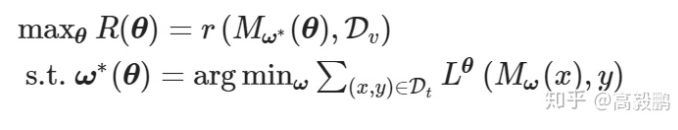
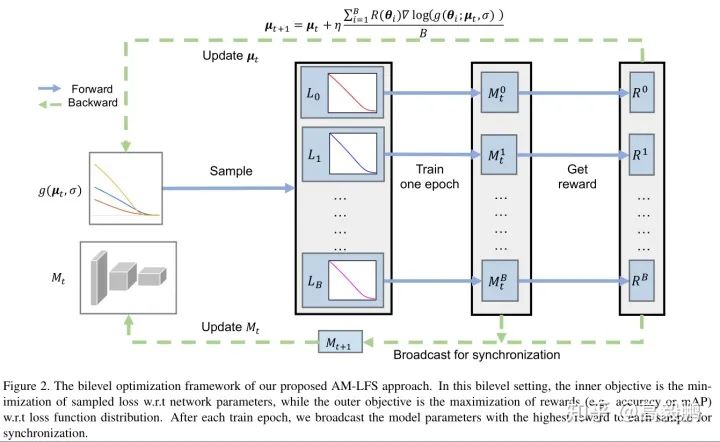
具体优化过程如下图所示：