一文读懂决策树
点击左上方蓝字关注我们

目录
决策树不确定性的度量方法
决策树的特征筛选准则
决策函数的损失函数评估
决策树最优模型的构建步骤
决策树的优缺点分析
决策树不确定性的度量方法
1. 不确定性的理解
下图为事件A是否发生的概率分布,事件发生记为1,讨论事件A的不确定性。
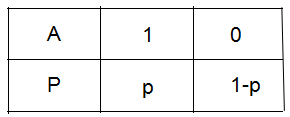
(1) 我们考虑一种极端的情况,若 p=1或 p=0,表示为事件A必定发生或事件A不可能发生,即不确定性为0。
(2) 若 p>1/2,即事件A发生的概率大于事件A不发生的概率,我们倾向于预测事件A是发生的;若 p<1/2,即事件A不发生的概率小于事件A发生的概率,我们倾向于预测事件A是不发生的。若 p=1/2,即事件A发生的概率等于事件A不发生的概率,我们无法作出预测,即事件A的不确定性达到最大,以致于我们无从预测,或者可以理解成事件A太复杂了,复杂的我们只能靠运气去猜测事件A是否发生。
2. 决策树不确定性的度量方法
本文用熵和基尼指数去衡量数据集的不确定性,假设数据集包含了K类,每个类的大小和比例分别为 Di 和 pi,i = 1,2,...K。
(1)熵的不确定性度量方法
在信息论和概率论统计中,熵是表示随机变量不确定性的度量,令熵为H(p),则:
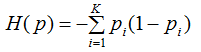
熵越大,数据集的不确定性就越大。
(2)基尼指数的不确定度量方法
数据集的基尼指数定义为:
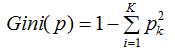
基尼指数越大,数据集的不确定性越大。
决策树的特征筛选准则
假设数据集A共有K个特征,记为xi,i=1,2,...K。数据集A的不确定性越大,则数据集A包含的信息也越多。假设数据集A的信息为H(A),经过特征xi筛选后的信息为H(A|xi),定义信息增益g(A,xi)为两者的差值,即:
g(A,xi) = H(A) - H(A|xi)
选择使数据集A信息增益最大的特征作为筛选特征,数学表示为:
x = max( g(A,xi) ) = max( H(A) - H(A|xi) )
决策树的损失函数评估
令决策树的叶节点数为T,损失函数为:
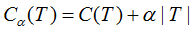
其中C(T)为决策树的训练误差,决策树模型用不确定性表示,不确定性越大,则训练误差亦越大。T表示决策树的复杂度惩罚,α参数权衡训练数据的训练误差与模型复杂度的关系,意义相当于正则化参数。
考虑极端情况:当α趋于0的时候,最优决策树模型的训练误差接近 0,模型处于过拟合;当α趋于无穷大的时候,最优决策树模型是由根节点组成的单节点树。
决策树最优模型的构建步骤
将数据集A通过一定的比例划分为训练集和测试集。
决策树的损失函数:
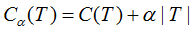
决策树最优模型的构建步骤包括训练阶段和测试阶段:
训练阶段:
(1)最小化决策树的不确定性值得到的生成模型,即决策树生成;
(2)通过决策树剪枝,得到不同的正则化参数α下的最优决策树模型,即决策树剪枝。
下面重点讨论训练阶段的决策树生成步骤和决策树剪枝步骤。
决策树生成步骤:
(1) 根据决策树的特征筛选准则,选择数据集信息增益最大的特征;
(2) 重复第一个步骤,直到所有叶节点的不确定性为0 。
决策树剪枝步骤:
(1) 将正则化参数α从小到大分成不同的区间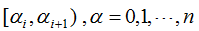 ,对决策树的非叶节点进行剪枝,令该节点为T,以该节点为根节点的子树为Tt。
,对决策树的非叶节点进行剪枝,令该节点为T,以该节点为根节点的子树为Tt。
(2) 当α满足如下条件时:
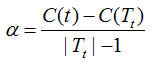
即节点为单节点树的损失函数与子树Tt的损失函数相等,而剪枝后的复杂度降低了,泛化性能较好,因此,对该节点进行剪枝。
(3)遍历所有非叶节点,得到每个剪枝后的最优子树与对应的α参数 。
备注:决策树生成和剪枝步骤只给出大致框架,具体请参考李航《统计学习方法》
测试阶段:
通过测试集评估不同α参数下的最优决策树模型,选择测试误差最小的最优决策树模型和相应的正则化参数α。
决策树的优缺点分析
优点:
算法简单,模型具有很强的解释性
可以用于分类和回归问题
缺点:
决策树模型很容易出现过拟合现象,即训练数据集的训练误差很小,测试数据集的测试误差很大,且不同的训练数据集构建的模型相差也很大。实际项目中,我们往往不是单独使用决策树模型,为了避免决策树的过拟合,需对决策树结合集成算法使用,如bagging算法和boosting算法。
参考:
李航《统计学习方法》
END
整理不易,点赞三连↓
