从有理数到实数和数的连续体
日期 : 2022年02月12日
正文共 :10551字
无理数或实数的定义; 实数集为什么是连续的、实数集里的数为什么可以和数轴上的点一一对应; 无理数的独特性质; 无理数为什么也满足有理数的运算法则和运算性质(如乘法结合律、分配律等);
第一部分 从有理数集到连续的实数集
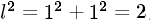 ,如果那个交点是有理点,那么l就应该是一个有理数,则l可以用这种形式唯一表示,即l=q,按规定p和q没有比1大的公因子,把l换成后有(p/q)^2=2,接下来我们将导出与此相悖的结论出来。稍作变换得到
,如果那个交点是有理点,那么l就应该是一个有理数,则l可以用这种形式唯一表示,即l=q,按规定p和q没有比1大的公因子,把l换成后有(p/q)^2=2,接下来我们将导出与此相悖的结论出来。稍作变换得到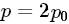 ,是整数,把前面等式的p换作
,是整数,把前面等式的p换作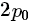 后有
后有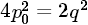 ,即
,即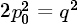 ,这说明是偶数,显然q也必须是偶数,这就证明了p和q有公因子2,这与前面的"p和q没有比1大的公因子"这个规定矛盾,而造成这种矛盾的起因就是我们一开始假设那个交点是有理点,所以数轴上的点并非都有有理数与之对应,可称没有有理数与之对应的点为"无理点",很容易能在数轴上构造出无数多个无理点出来。
,这说明是偶数,显然q也必须是偶数,这就证明了p和q有公因子2,这与前面的"p和q没有比1大的公因子"这个规定矛盾,而造成这种矛盾的起因就是我们一开始假设那个交点是有理点,所以数轴上的点并非都有有理数与之对应,可称没有有理数与之对应的点为"无理点",很容易能在数轴上构造出无数多个无理点出来。第二部分 定义实数的方式
第三部分 回顾Dedekind对实数的定义方式

Courant and Robbins, What Is Mathematics? Second Edition, P60↩ John Stillwell, Numbers and Geometry, P260↩ Richard Dedekind, Essays on the Theory of Numbers, P5↩ Richard Dedekind, Essays on the Theory of Numbers, P5↩ Richard Dedekind, Essays on the Theory of Numbers, P9↩ Richard Courant, Fritz John, Introduction to Calculus and Analysis Volume I, Reprint of the 1989 edition, P2↩ Terence Tao, Analysis I, third edition, P117↩ David French Belding, Kevin J. Mitchell, Foundations of Analysis, 2nd Edition, P21↩ David French Belding, Kevin J. Mitchell, Foundations of Analysis, 2nd Edition, P21↩ Morris Kline, Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, P984↩ Morris Kline, Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, P986↩ D.C. Goldrei, Classic Set Theory: For Guided Independent Study,P8↩ Morris Kline, Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, P987↩ P. Ehrlich,Real Numbers, Generalizations of the Reals, and Theories of Continua, page x↩ Hans Niels Jahnke ,A History of Analysis,P306↩ S. C. Malik, Principles of Real Analysis,P18↩ Courant and Robbins, What Is Mathematics? Second Edition, P71↩ Rudiments of Mathematics Part 1, Academic Publishers,P15↩ Richard Dedekind, Essays on the Theory of Numbers, P7↩ Morris Kline, Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, P986↩
— THE END —

评论
