DIoU 和 CIoU 的原理与代码
共 4546字,需浏览 10分钟
·
2022-12-04 13:16
本篇接着上篇 交并比(IoU 与 GIoU 原理与实现) 继续,上篇介绍了 IoU 和 GIoU,本篇分享 DIoU 和 CIoU 的原理与实现。
DIoU 原理与实现
DIoU 原理
GIoU 虽然解决了 IoU 的一些问题,但是它并不能直接反映预测框与目标框之间的距离,DIoU(Distance-IoU)即可解决这个问题,它将两个框之间的重叠度、距离、尺度都考虑了进来。DIoU的计算公式如下:
其中, 和 分别代表两个框的中心点, 代表两个中心点之间的欧式距离, 代表两个图像的最小外接矩形的对角线,如图 1 所示。
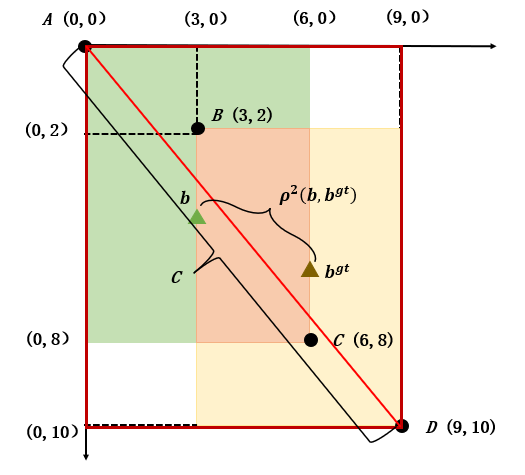
DIoU 相较于其他两种计算方法的优点是:
DIoU 可直接最小化两个框之间的距离,所以作为损失函数时 Loss 收敛更快。
在两个框完全上下排列或左右排列时,没有空白区域,此时 GIoU 几乎退化为了 IoU,但是 DIoU 仍然有效。
所以,DIoU 在完善图像重叠度的计算功能的基础上,实现了对图形距离的考量,但仍无法对图形长宽比的相似性进行很好的表示。
DIoU 计算
在图 2 中,通过计算可得,中心点 、中心点 的坐标分别为:
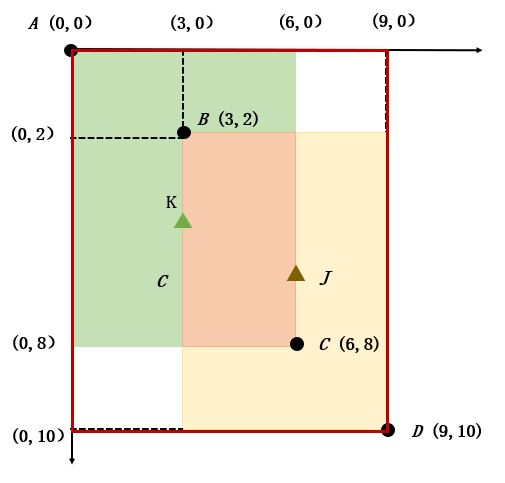
此时的 DIoU 计算公式为:
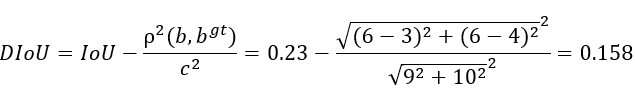
DIoU 实现
代码如下:
import numpy as np
import IoU
# box : [左上角x坐标,左上角y坐标,右下角x坐标,右下角y坐标]
box1 = [0, 0, 6, 8]
box2 = [3, 2, 9, 10]
# DIoU
def DIoU(box1, box2):
# 计算对角线长度 C
x1, y1, x2, y2 = box1
x3, y3, x4, y4 = box2
# numpy.sqrt() 函数计算给定数组中每个元素的平方根。
C = np.sqrt((max(x2, x4) - min(x1, x3)) ** 2 +
(max(y2, y4) - min(y3, y1)) ** 2)
print('C: ', C)
# box1 中心点x坐标: x2 - (x2 - x1) / 2
point1_x, point1_y = (x2 + x1) / 2, (y2 + y1) / 2
# box2 中心点
point2_x, point2_y = (x4 + x3) / 2, (y4 + y3) / 2
# 计算中心点间距 D
D = np.sqrt((point2_x - point1_x) ** 2 +
(point2_y - point1_y) ** 2)
# 计算IoU,调用IoU(box1, box2)函数
iou = IoU(box1, box2)
diou = iou - (D ** 2 / C ** 2)
return diou
print(DIoU(box1,box2))
CIoU 原理与实现
CIoU 原理
CIoU 的全称为 Complete IoU,它在 DIoU 的基础上,还同时考虑两个矩形的长宽比,也就是形状的相似性。CIoU 的计算公式为:
其中, 是权重函数,而 用来度量长宽比的相似性。计算公式为:
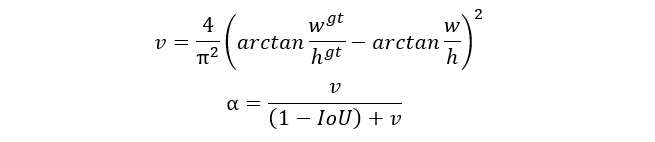
可以看出,CIoU 就是在 DIoU 的基础上,增加了图像相似性的影响因子,因此可以更好地反映两个框之间的差异性。
还需要注意的一点是,在使用 CIoU 作为 Loss 的时候, 的梯度同样会参与反向传播的计算,其中:
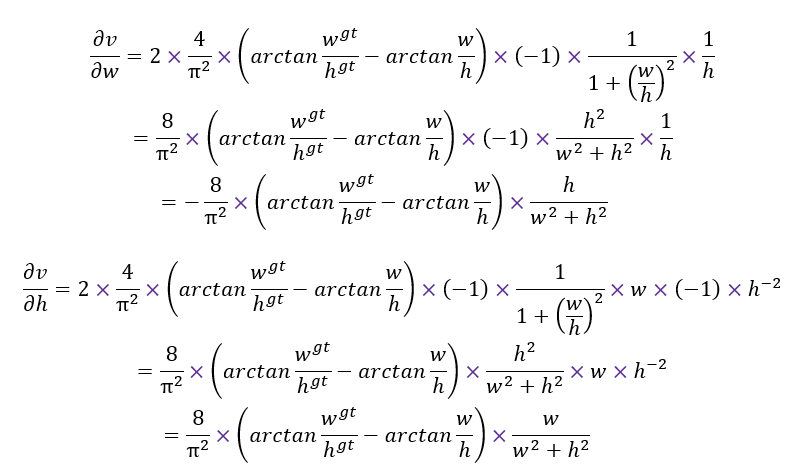
如果矩形的 和 均小于1, 的值则会很小,这样很容易出现梯度爆炸的现象,所以在计算 的梯度时,直接把 当做 1 来计算。论文里会在 关于 和 的偏导数上加负号。
至此,IoU 终于实现了对两个图像之间的重叠比例、图形距离、形状相似度(矩形长宽比)的综合度量。
CIoU 计算
继续以图 2 为例,中心点 、中心点 的坐标分别为:
此时 CIoU 的计算公式为:
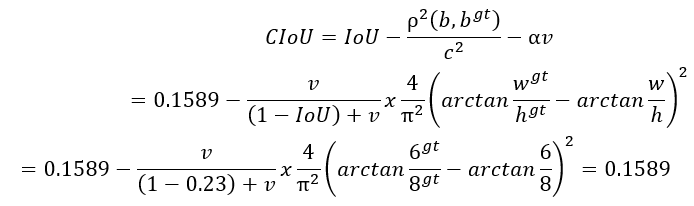
由于最开始设定的两个矩形的形状相同,计算所得的形状惩罚项为 0,因此此时 CIoU=DIoU 。由此可见,两个形状差别越大,CIoU 相较于 DIoU 越小。
CIoU 实现
代码如下:
import numpy as np
import IoU
import DIoU
# box : [左上角x坐标,左上角y坐标,右下角x坐标,右下角y坐标]
box1 = [0, 0, 6, 8]
box2 = [3, 2, 9, 10]
# CIoU
def CIoU(box1, box2):
x1, y1, x2, y2 = box1
x3, y3, x4, y4 = box2
# box1的宽:box1_w,box1的高:box1_h,
box1_w = x2 - x1
box1_h = y2 - y1
# box2的宽:box2_w,box2的高:box2_h,
box2_w = x4 - x3
box2_h = y4 - y3
iou = IoU(box1, box2)
diou = DIoU(box1, box2)
# v用来度量长宽比的相似性
v = (4 / (np.pi) ** 2) * (np.arctan(int(box2_w / box2_h)) - np.arctan(int(box1_w / box1_h)))
# α是权重函数
a = v / ((1 + iou) + v)
ciou = diou - a * v
return ciou
print(CIoU(box1, box2))
今天分享了 DIoU 和 CIoU 的原理和代码,后台回复 IoU,即可获得 IoU、GIoU、DIoU 和 CIoU 的代码。
最后祝大家有所进步!
参考文献
[1] 理解梯度:https://www.cnblogs.com/zzzzy/p/8505150.html
[2] Generalized Intersection over Union:https://arxiv.org/pdf/1902.09630.pdf
[3] Distance-IoU Loss: https://arxiv.org/pdf/1911.08287.pdf
[4] 交并比(IoU 与 GIoU 原理与实现)
