HDU2050 折线分割平面(递推)
HDU2050 折线分割平面(递推)
Problem Description
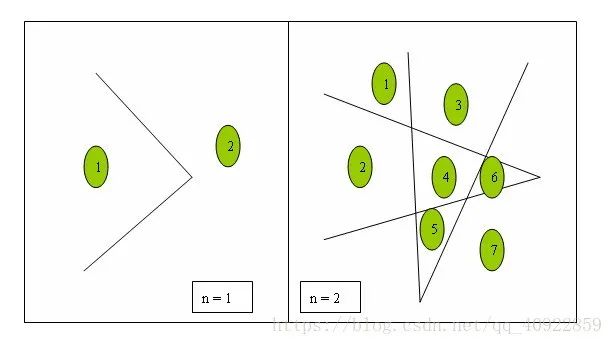
我们看到过很多直线分割平面的题目,今天的这个题目稍微有些变化,我们要求的是n条折线分割平面的最大数目。比如,一条折线可以将平面分成两部分,两条折线最多可以将平面分成7部分,具体如下所示。
Input
输入数据的第一行是一个整数C,表示测试实例的个数,然后是C 行数据,每行包含一个整数n(0<n<=10000),表示折线的数量。
Output
对于每个测试实例,请输出平面的最大分割数,每个实例的输出占一行。
Sample Input
2 1 2
Sample Output
2 7

分析如下:
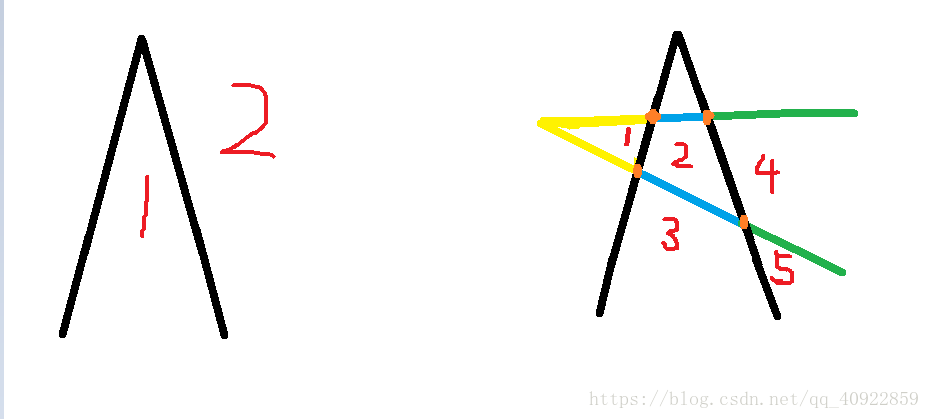
对于第n-1条折线,它把空间划分的区域为f(n-1),为了让增加的区域更多,新增的折线要和之前的n-1条折线的2*(n-1)条边都相交,产生4*(n-1)条新的线段(图中黄蓝),每条线段或射线(绿)产生一个新区域,但是折线的头(黄色)的两线段一共只能产生一个区域,所以新增区域的数量为4*(n-1) -1+2 即 4*(n-1) +1 ;
所以有递推公式:
f(n)=f(n-1)+4(n-1) + 1;
=f(n-2)+4(n-2)+4(n-1)+2;
.......
=f(n-(n-1)) +4(n-(n-1))+4(n-(n-2))+......+4(n-1) + n-1;
=f(1) +4(1+2+3+4+....+n-1)+n-1;
=2+4((n-1)(n-1+1)/2)+n-1;
=2n^2-n+1;
代码:
#include<stdio.h>
typedef long long ll;
int main()
{
int t;
scanf("%d",&t);
ll n;
while(t--)
{
scanf("%d",&n);
printf("%d\n",2*n*n-n+1);
}
return 0;
}
评论
