HashMap 的设计与优化
愿天堂没有BUG
共 30515字，需浏览 62分钟
· 2021-08-19
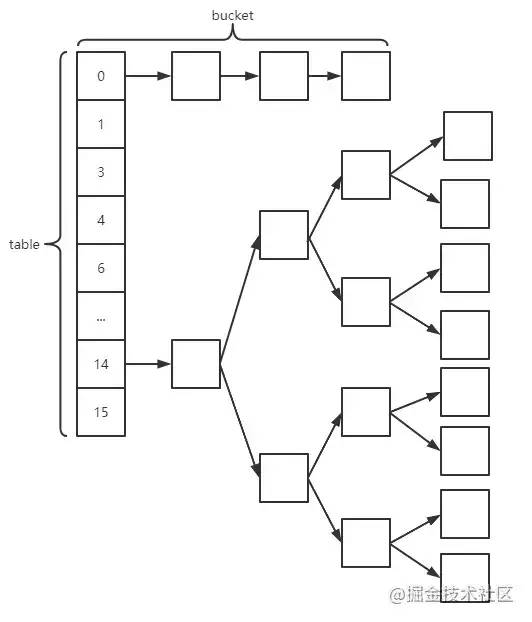
hashmap 是一个 key-value 形式的键值对集合。（本文内容基于 JDK1.8）下面是一个简单的 hashmap 的结构。本文主要是通过源码的方式分析 HashMap 的实现和优化。主要是围绕源码本身展开，以添加注释的方式进行记录和分析
初始化
在创建 HashMap 对象示例的时候不会初始化存储数组，会在首次调用 put 方法的时候初始化数组。构造方法如下：
public HashMap(int initialCapacity, float loadFactor) {
// initialCapacity 初始容量 < 0 报错; 默认 16
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
// initialCapacity 初始容量是否大于最大容量
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
// loadFactor 负载因子 <= 0 || isNaN ; 默认0.75
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}
复制代码put 方法
添加数据通常我们采用 put 方法，该方法也是我们开发中比较常用的方法之一。最终会调用 putVal 方法进行初始化和添加数据。在这个方法中我们需要注意的有几个地方：
如果没有初始化会调用 resize() 方法进行 hashmap 存储数组的初始化。
默认通过 & 运算计算节点存储位置，这里也证明了为什么初始化数组的长度要是 2 的 n 次方。
如果不存在 hash 冲突的情况下，通过然后调用 newNode 方法创建节点，存放到对应的数组下标。
如果存在 hsah 冲突的情况下。这里就会有三种情况：
首次 hash 冲突的情况下，当前节点是一个普通的节点，如果 key 相同得话，将采取数据覆盖的方式；
如果当前节点类型是 treeNode 类型，是一棵红黑树。将调用 putTreeVal 方法来进行添加子节点；
最后，将当作链表处理，首先查找链表的尾节点，找到尾节点后，将当前节点添加到尾节点，这里有一个判断如果当前链表的节点数 > 8 并且 hashmap 的总长度 > 64 就会将当前的链表进行变换为红黑树。还有一种特殊情况，如果在链表的查找过程中查找到了一个当前新增key 相同的节点，那么就会覆盖当前节点数据并且退出循环；
前面所有的步骤都是为了找到当前的节点指针，然后再通过当前对象修改 value 值， 这里有一个需要注意的地方，在修改的时候会做一个判断如果
**_onlyIfAbsent_**等于 false 才可以修改，就是说可能当前 hashmap 存在不可以被修改的情况，比如：map.putIfAbsent 方法的时候调用就会修改失败，最后才能修改 value 值，并且返回旧值。最后对修改次数累加，然后判断一次是否需要拓展 hashmap 的容量，然后返回 null , 方法结束。
// put 方法
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
// putVal 方法
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
// 如果没有初始化
if ((tab = table) == null || (n = tab.length) == 0)
// 调用 resize 初始化
// n = tab.length 容量
n = (tab = resize()).length;
// 默认通过 & 运算计算节点存储位置，这里也证明了为什么初始化数组的长度要是2的n 次方
// 并且把当前节点的数据给 p
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
// 如果节点数据已经存在，即存在 hash 冲突的情况
Node<K,V> e; K k;
// 1. 当前节点存在，并且插入k，和存在的 k 的value 值相同，那么直接刷新当前节点数据即可
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
// 新的节点数据 = p, 其实这里也只是获取 p 的指针
e = p;
// 2. 如果是 TreeNode 结构， 即红黑树结构
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
// 3. 其他情况，即链表结构
for (int binCount = 0; ; ++binCount) {
// 父节点子节点为 null
if ((e = p.next) == null) {
// 将 p.next = newNode
p.next = newNode(hash, key, value, null);
// 节点数是否大于变形的阈值 (TREEIFY_THRESHOLD = 8)
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
// 如果 tab.length < 64 默认拓容
// 否则进行红黑树转换
treeifyBin(tab, hash);
break;
}
// 如果存在值相同的情况
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
// 如果 e 不为空，就是说当前节点指针不为空，【这种情况是覆盖】，返回旧值
if (e != null) { // existing mapping for key
V oldValue = e.value;
// 当前节点可以被修改或者是新增节点
if (!onlyIfAbsent || oldValue == null)
e.value = value;
// 预留模板方法
afterNodeAccess(e);
return oldValue;
}
}
// 修改次数 ++
++modCount;
// 大于拓容阈值
if (++size > threshold)
// 拓容
resize();
// 预留模板方法
afterNodeInsertion(evict);
return null;
}
复制代码总结：其实通过上面的分析和代码的，我们分析出有一下几个核心方法：
newNode创建 Node 节点((TreeNode<K,V>)p).putTreeVal(**this**, tab, hash, key, value);添加节点信息；treeifyBin节点冲突情况下，链表转换为红黑树；resize()HashMap 拓容；
newNode 创建节点
创建 HashMap 的节点信息，其实这个方法看上去比较普通，但是本质上也是比较普通。但是对于 hash 这个参数我们可以思考一下。
Node<K,V> newNode(int hash, K key, V value, Node<K,V> next) {
return new Node<>(hash, key, value, next);
}
复制代码hash 计算 hash 码
hash 方法如下，
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
复制代码理论上 hash 散列是一个 int 值，如果直接拿出来作为下标访问 hashmap 的话，考虑到二进制 32 位，取值范围在**-2147483648 ~ 2147483647** 范围。大概有 40 亿个 key ， 只要哈希函数映射比较均匀松散，一般很难出现碰撞。存在一个问题是 40 亿长度的数组，内存是不能放下的。因为咱们 HashMap 的默认长度为 16 。所以这个 hashCode , (key.hashCode ) 是不能直接来使用的。使用之前先做对数组长度的与运算，得到的值才能用来访问数组下标。代码如下：
// n = hashmap 的长度
p = tab[i = (n - 1) & hash])
复制代码这里为什么要使用 n -1 ，来进行与运算，这里详单与是一个”低位掩码”, 以默认长度 16 为例子。和某个数进行与预算，结果的大小是 < 16 的。如下所示：
10000000 00100000 00001001
& 00000000 00000000 00001111
------------------------------
00000000 00000000 00001001 // 高位全部归 0, 只保留后四位
复制代码这个时候会有一个问题，如果本身的散列值分布松散，只要是取后面几位的话，碰撞也会非常严重。还有如果散列本省做得不好的话，分布上成等差数列的漏洞，可能出现最后几位出现规律性的重复。这个时候“扰动函数”的价值制就体现出来了。如下所示：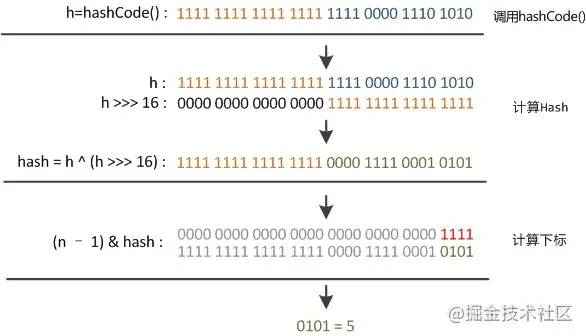
在 hash 函数中有这样的一段代码：(h = key.hashCode()) ^ (h >>> 16) 右位移 16 位， 正好是32bit 的一半，与自己的高半区做成异或，就是为了**混合原始的哈希码的高位和低位，以此来加大低位的随机性。**并且混合后的低位掺杂了高位的部分特征，这样高位的信息变相保存下来。其实按照开发经验来说绝大多数情况使用的时候 hashmap 的长度不会超过 1000，所以提升低位的随机性可以提升可以减少hash 冲突，提升程序性能。
如果感兴趣的小伙伴可以浏览下一下 Peter Lawlay 的专栏《An introduction to optimising a hashing strategy》
Node.putTreeVal
当前是一棵红黑树那么就需要添加节点
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
int h, K k, V v) {
Class<?> kc = null;
boolean searched = false;
TreeNode<K,V> root = (parent != null) ? root() : this;
for (TreeNode<K,V> p = root;;) {
int dir, ph; K pk;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) {
if (!searched) {
TreeNode<K,V> q, ch;
searched = true;
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q;
}
dir = tieBreakOrder(k, pk);
}
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
Node<K,V> xpn = xp.next;
TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
if (dir <= 0)
xp.left = x;
else
xp.right = x;
xp.next = x;
x.parent = x.prev = xp;
if (xpn != null)
((TreeNode<K,V>)xpn).prev = x;
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}
复制代码treeifyBin 链表树化
如果 hashmap 的长度小于 64 会优先选择拓容，否则会当前冲突 key 所在的结构由链表转换为红黑树。这个是 jdk 1.8 才有的新特征，hashmap 在 hash 冲突后可能由链表变化为红黑树结构。这样做的目的是为了提高读写效率。
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
// 不一定树化还可能是拓容，需要看数组的长度是否小于 64 MIN_TREEIFY_CAPACITY
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
else if ((e = tab[index = (n - 1) & hash]) != null) {
// hd 头节点, tl 尾节点
TreeNode<K,V> hd = null, tl = null;
do {
// 将链表转换为树结构
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
if ((tab[index] = hd) != null)
// 转换红黑树操作，这里循环比较，染色、旋转等
hd.treeify(tab);
}
}
复制代码replacementTreeNode 方法
replacementTreeNode 方法主要是将 Node 转换为 TreeNode
TreeNode<K,V> replacementTreeNode(Node<K,V> p, Node<K,V> next) {
return new TreeNode<>(p.hash, p.key, p.value, next);
}
复制代码TreeNode#treeify 方法
treeify 方法主要是将树结构转换为红黑树。
final void treeify(Node<K,V>[] tab) {
// 根节点默认为 null
TreeNode<K,V> root = null;
// 链表遍历，x 指向当前节点，next 指向下一个节点
for (TreeNode<K,V> x = this, next; x != null; x = next) {
// 下一个节点
next = (TreeNode<K,V>)x.next;
// 设置当前节点的 left, right 为 null
x.left = x.right = null;
// 如果没有根节点
if (root == null) {
// 当前父节点为 null
x.parent = null;
// 当前红色节点属性设置为 false (把当前节点设置为黑色)
x.red = false;
// 根节点指向当前节点
root = x;
}
// 如果已经存在根节点
else {
// 获取当前链表的 key
K k = x.key;
// 获取当前节点的 hash
int h = x.hash;
// 定义当前 key 所属类型
Class<?> kc = null;
// 从根节点开始遍历，此遍历设置边界，只能从内部跳出
for (TreeNode<K,V> p = root;;) {
// dir 标识方向（左右）ph 标识当前节点的 hash 值
int dir, ph;
// 当前节点的 key
K pk = p.key;
// 如果当前节点 hash 值大于当前 链表节点的 hash 值
if ((ph = p.hash) > h)
// 标识当前节链表节点会放在当前红黑树节点的左侧
dir = -1;
else if (ph < h)
// 右侧
dir = 1;
// 如果两个节点的 key 的 hash 值相等，那么通过其他方式进行比较
// 如果当前链表节点的 key 实现了comparable 接口，并且当前树节点和链表节点是相同的 class 实例，那么通过 comparable 比较
// 如果还是相等再通过 tieBreakOrder 比较一次
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
TreeNode<K,V> xp = p; // 保存当前树节点
// 如果 dir 小于等于 0: 当前链表节点一定放置在当前树节点的左侧，但不一定是该树节点的左子节点，
// 也可能是左子节点或者右子节点或者更深层次的节点
// 如果dir 大于等于 0: 当前链表节点一定放置在当前树节点的右侧，但不一定是该树节点的右子节点，
// 也可能是右子节点或者左子节点或者更深层次的节点
// 如果当前树节点不是叶子，那么最终以当前树节点的左子节点或者右子节点为起始几点，然后再重新开始寻找自己当前链表节点的位置。
// 如果当前树节点就是叶子节点，那么更具 dir 的值，就可以把当前链表节点挂载到当前树节点的左或者右侧了。
// 挂载之后，还需要重新把树进行平衡。平衡之后，就可以针对下一个链表节点进行处理了
if ((p = (dir <= 0) ? p.left : p.right) == null) {
x.parent = xp; // 当前链表节点作为当前树节点的子节点
if (dir <= 0)
xp.left = x; // 左子节点
else
xp.right = x; // 右子节点
root = balanceInsertion(root, x); // 重新平衡
break;
}
}
}
}
// 把所有的链表节点都遍历之后，最终构造出来的树可能是经历多个平衡操作，根节点目前到底是链表的那个节点是不确定的
// 因为我们需要基于树来做查找，所以就应该把 tab[N] 得到的对象一定是根节点对象，而且是链表的第一个节点对象，所以要做对应的调整。
// 把红黑树的节点设置为所在数组槽的第一个元素
// 说明: TreeNode 既是一个红黑树也是一个双向链表
// 这个方法做的事情是保证树根节点一定要成为链表的首节点
moveRootToFront(tab, root);
}
复制代码balanceInsertion 树平衡
这个方法分析之前，我们可以先看看红黑树的规则：红黑树是每个结点都带有颜色属性的二叉查找树，颜色或红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:
性质1. 节点是红色或黑色。
性质2. 根节点是黑色。
性质3. 所有叶子都是黑色。（叶子是NIL结点）
性质4. 每个红色节点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色节点）
性质5. 从任一节节点其每个叶子的所有路径都包含相同数目的黑色节点。
// root 为根节点
// x 为需要插入的节点
// 最后返回的是一个平很后的根节点
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
// 查询节点标记为红色
x.red = true;
// 设置一个只可以内部退出的循环
// 变量说明:
// xp 当前节点, xpp 父节点的父节点, xppl 父节点的父节点的左节点, xppr 父节点的父节点的右节点
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
// 如果父节点为空， 说明当前节点就是根节点，那么直接把当前接待你标记为黑色返回当前节点。
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
// 如果当前节点为黑设色并且当前父节点为 null, 或者
// 父节点为红色，但是 xpp 节点为空
else if (!xp.red || (xpp = xp.parent) == null)
return root;
// 当前节点等于 xppl
if (xp == (xppl = xpp.left)) {
//xppr != null 并且 是红色
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp; // 当前节点等于 xpp, 进入下一次循环
}
else {
if (x == xp.right) { // 当前节点是父节点的右子节点
root = rotateLeft(root, x = xp); //父节点左旋
xpp = (xp = x.parent) == null ? null : xp.parent; // 获取 xpp
}
if (xp != null) { // 父节点不为空
xp.red = false; // 父节点设置为黑色
if (xpp != null) { // xpp 不为空
xpp.red = true; // xpp 为红色
root = rotateRight(root, xpp); // xpp 右旋转
}
}
}
}
else { // 如果 xp 是 xpp 的右节点
if (xppl != null && xppl.red) { // xppl 不为空，并且为红色
xppl.red = false; // xppl 设置为黑色
xp.red = false; // 父节点为黑色
xpp.red = true; // xpp 为红色
x = xpp; // x = xpp 进入下次循环
}
else {
if (x == xp.left) { // 当前节点为父节点的左子节点
root = rotateRight(root, x = xp); // 根节点你右旋转
xpp = (xp = x.parent) == null ? null : xp.parent; // xpp = xp.parent
}
if (xp != null) { // xp != null
xp.red = false; // xp 为黑色
if (xpp != null) { // xpp != null
xpp.red = true; // xpp 为红色
root = rotateLeft(root, xpp); // 左旋
}
}
}
}
}
}
// 节点左旋转
// root 当前根节点
// p 指定选装的节点
// 返回旋转后的根接待你（平衡涉及左旋右旋根根节点改变，所以需要返回最新的根节点）
// 示意图
// pp pp
// | |
// p ---> r
// / \ / \
// l r p rr
// / \ / \
// rl rr l rl
// 旋转做了几件事情？
// 1. 将 rl 设置为 p 的子接待你，将 rl 设置为父节点 p
// 2. 将 r 的父节点设置 pp, 将 pp 的左子节点设或者右子接待你设置为 r
// 3. 将 r 的左子节点设置为 p, 将 p 的父节点设置为 r
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> r, pp, rl;
// 左旋的节点以及需要左旋的节点的右节点不为空
if (p != null && (r = p.right) != null) {
// 要左旋转的右子节点 = rl ,
if ((rl = p.right = r.left) != null)
// 设置 rl 父亲节点设置为 p
rl.parent = p;
// 将 r 的父节点设置为 p 的父节点，如果 pp == null
if ((pp = r.parent = p.parent) == null)
// 染黑
(root = r).red = false;
else if (pp.left == p) // 判断父节点是在 pp 的左边还是右边
pp.left = r; // 如果是左子节点，把 pp.letf = r
else
pp.right = r; // 如果是右子节点, pp.reight = r
r.left = p; // 最后将 r的左子节点设置为 p
p.parent = r; // 最后将 p.parent 设置为 r
}
return root;
}
// 节点右旋转
// 右旋同理
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> l, pp, lr;
if (p != null && (l = p.left) != null) {
if ((lr = p.left = l.right) != null)
lr.parent = p;
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
l.right = p;
p.parent = l;
}
return root;
}
复制代码moveRootToFront 方法
把所有的链表节点都遍历之后，最终构造出来的树可能是经历多个平衡操作，根节点目前到底是链表的那个节点是不确定的。因为我们需要基于树来做查找，所以就应该把 tab[N] 得到的对象一定是根节点对象，而且是链表的第一个节点对象，所以要做对应的调整。把红黑树的节点设置为所在数组槽的第一个元素，这个方法做的事情是保证树根节点一定要成为链表的首节点。
static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {
int n;
// root 节点不为空， 并且表不为空， 并且数组长度大于 0
if (root != null && tab != null && (n = tab.length) > 0) {
// 当前 Node 所在槽位
int index = (n - 1) & root.hash;
// 获取当前槽所在接待你
TreeNode<K,V> first = (TreeNode<K,V>)tab[index];
// 如果当前槽位节点不是首节点
if (root != first) {
// 后驱节点
Node<K,V> rn;
// 修改为首节点
tab[index] = root;
// rp 前驱节点为 root 的前驱节点
TreeNode<K,V> rp = root.prev;
// 后驱节点不为空
if ((rn = root.next) != null)
((TreeNode<K,V>)rn).prev = rp;
if (rp != null)
rp.next = rn;
if (first != null)
// 原来的头节点前驱节点指向新的头节点 root 节点
first.prev = root;
// root 节点的后驱节点指向之前的头节点
root.next = first;
// root 由于是头节点所以前驱节点为 null
root.prev = null;
}
assert checkInvariants(root);
}
}
复制代码remove 方法
remove 方法的本质是将 key 值所在的节点的值设置为 nu
public V remove(Object key) {
Node<K,V> e;
return (e = removeNode(hash(key), key, null, false, true)) == null ?
null : e.value;
}
复制代码removeNode 方法
final Node<K,V> removeNode(int hash, Object key, Object value,
boolean matchValue, boolean movable) {
Node<K,V>[] tab; Node<K,V> p; int n, index;
// tab 不为空, 数组长度大于 0, 当前节点数据不为 null
// 不得不说 hashmap 源码的逻辑还是非常严谨的
if ((tab = table) != null && (n = tab.length) > 0 &&
(p = tab[index = (n - 1) & hash]) != null) {
// node 用来存储当前节点信息
Node<K,V> node = null, e; K k; V v;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
node = p;
else if ((e = p.next) != null) {
// 如果是树形结构
if (p instanceof TreeNode)
// 获取节点
node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
else {
// 链表查找
do {
if (e.hash == hash &&
((k = e.key) == key ||
(key != null && key.equals(k)))) {
node = e;
break;
}
p = e;
} while ((e = e.next) != null);
}
}
//
if (node != null && (!matchValue || (v = node.value) == value ||
(value != null && value.equals(v)))) {
// 如果是红黑树，删除节点
if (node instanceof TreeNode)
((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
else if (node == p) // 如果是头节点
// 那么头节点指针指向移除节点的后驱节点
tab[index] = node.next;
else
// 前驱节点的后驱指针，指向当前节点的后驱指针
p.next = node.next;
// 修改次数累加
++modCount;
// 数据长度减少
--size;
afterNodeRemoval(node);
return node;
}
}
return null;
}
复制代码removeTreeNode 方法
removeTreeNode 是删除节点的核心方法，删除的时候如果是一个普通节点就可以直接情况，如果是链表的话需要将当前节点删除。如果是红黑树的话，需要删除 TreeNode , 然后进行一次树平衡，或者将树转换为链表。
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,
boolean movable) {
int n;
if (tab == null || (n = tab.length) == 0)
return;
// 获取索引值
int index = (n - 1) & hash;
// 获取头节点，即树的根节点
TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;
// 当前节点的后驱节点，当前节点的前驱节点保存
TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;
// 前驱节点为 null
if (pred == null)
// 当前是头节点，删除之后，头节点直接指向了删除节点的后继节点
tab[index] = first = succ;
else
pred.next = succ;
if (succ != null)
succ.prev = pred;
// 如果头节点（即根节点）为空，说明当前节点删除后，红黑树为空，直接返回
if (first == null)
return;
// 如果头接单不为空，直接调用 root() 方法获取根节点
if (root.parent != null)
root = root.root();
if (root == null
|| (movable
&& (root.right == null
|| (rl = root.left) == null
|| rl.left == null))) {
// 链表化，英文前面的链表节点完成删除操作，故这里直接返回，即可完成节点删除
tab[index] = first.untreeify(map); // too small
return;
}
// p 当前节点; pl 当前节点左节点，pr 当前节点右节点
// replacement p 节点删除后替代的节点
TreeNode<K,V> p = this, pl = left, pr = right, replacement;
if (pl != null && pr != null) {
// p 节点删除后， 他的左右节点不为空时， 遍历他的右节点上的左子树
// （以下操作先让 p 节点和 s 节点交换位置，然后再找到 replacement 节点替换他 ）
TreeNode<K,V> s = pr, sl;
while ((sl = s.left) != null) // find successor
s = sl;
// 通过上述操作 s 节点是大于 p 节点的最小节点（替换它的节点）
// 将 s 节点和 p 节点的颜色交换
boolean c = s.red; s.red = p.red; p.red = c; // swap colors
// sr s 节点的右节点
TreeNode<K,V> sr = s.right;
// pp p 节点的父节点
TreeNode<K,V> pp = p.parent;
// 如果 pr 就是 s 节点
if (s == pr) { // p was s's direct parent
// 节点交换
p.parent = s;
s.right = p;
}
else {
// 获取 s 的父节点
TreeNode<K,V> sp = s.parent;
// 将 p 节点的父节点指向 sp, 且 sp 节点存在
if ((p.parent = sp) != null) {
// 判断 s 节点的 sp 节点在左侧还是右侧， 将 p 节点存放在 s 节点一侧
if (s == sp.left)
sp.left = p;
else
sp.right = p;
}
// 将 pr 节点编程 s 节点的右节点，并且 pr 节点存在
if ((s.right = pr) != null)
// 将 s 节点编程 pr 节点的父节点
pr.parent = s;
}
// 因为 s 节点的性质， s 节点没有左节点
// 当 p 节点和 s 节点交换了位置，所以将 p 节点的左几点指向空
p.left = null;
// 将 sr 节点编程 p 节点的左节点，并且 sr 节点存在
if ((p.right = sr) != null)
// 将 p 节点编程 sr 的父节点
sr.parent = p;
// 将 pl 节点编程 s 节点的左节点，并且存在 pl 节点
if ((s.left = pl) != null)
// 将 pl 父节点赋值为s
pl.parent = s;
// s 父节点设置为 pp 并且 pp 节点存在
if ((s.parent = pp) == null)
// root 节点为 s
root = s;
// p 节点等于 pp.left
else if (p == pp.left)
// pp 的左节点为 s
pp.left = s;
else
// p 节点等于 pp.right
// pp 右节点为 s
pp.right = s;
// sr 不为空
if (sr != null)
// 替换节点为 sr
replacement = sr;
else
// 否则替换节点为 p
replacement = p;
}
else if (pl != null)
// 如果 pl 节点存在， pr 节点不存在，不用交换位置， pl 节点为替换为 replacement 节点
replacement = pl;
else if (pr != null)
// 如果 pr 节点存在, pl 节点不存在， 不用交换位置， pr 节点为替换为 replacement 节点
replacement = pr;
else
// 如果都不存在 p 节点成为 replacement 节点
replacement = p;
// 以下判断根据上述逻辑查看，仅以p 节点的当前位置为性质， 对 replacement 节点进行操作
if (replacement != p) {
// 如果 replacement 不是 p 节点
// 将 p 节点的父节点 pp 变成 replacement 节点的父节点
TreeNode<K,V> pp = replacement.parent = p.parent;
// 如果 pp 节点不存在
if (pp == null)
// replacement 变成根节点
root = replacement;
else if (p == pp.left)
// 如果 pp 节点存在，根据 p 节点在 pp 节点的位置，设置 replacement 节点的位置
pp.left = replacement;
else
pp.right = replacement;
// 将 p 节点所有的引用关系设置为 null
p.left = p.right = p.parent = null;
}
// 如果 p 节点是红色，删除后不影响 root 节点，如果是黑色，找到平衡后的根节点，并且用 r 表示
TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);
// 如果 p 是 replacement 节点
if (replacement == p) { // detach
// 得到 pp
TreeNode<K,V> pp = p.parent;
p.parent = null;
if (pp != null) {
// pp 存在
// 根据 p 节点的位置，将 pp 节点的对应为位置设置为空
if (p == pp.left)
pp.left = null;
else if (p == pp.right)
pp.right = null;
}
}
// 移动新的节点到数组上
if (movable)
moveRootToFront(tab, r);
}
复制代码balanceDeletion 方法
删除节点后的树平衡方法 。
static <K,V> TreeNode<K,V> balanceDeletion(TreeNode<K,V> root,
TreeNode<K,V> x) {
// x 当前需要删除的节点
// xp x 父节点
// xpl x 父节点的左子节点
// xpr x 父节点的右子节点
for (TreeNode<K,V> xp, xpl, xpr;;) {
if (x == null || x == root)
// x 为空或者 x 为根节点
return root;
else if ((xp = x.parent) == null) {
// 当 xp 为空，说明 x 为根节点，将 x 设置为黑色并且返回 x 节点。
x.red = false;
return x;
}
else if (x.red) {
// x节点是红色，无需调整
x.red = false;
return root;
}
else if ((xpl = xp.left) == x) {
// 如果x节点为xpl节点
if ((xpr = xp.right) != null && xpr.red) {
// 如果xpr节点不为空，且xpr节点是红色的
// 将xpr设置为黑色，xp设置为红色
xpr.red = false;
xp.red = true;
// 左旋
root = rotateLeft(root, xp);
// 重新将xp节点指向x节点的父节点，并将xpr节点指向xp的右节点
xpr = (xp = x.parent) == null ? null : xp.right;
}
if (xpr == null)
// 若xpr节点不存在
// 则将x节点指向xp节点向上调整
x = xp;
else {
// sl xpr节点的左节点
// sr xpr节点的右节点
TreeNode<K,V> sl = xpr.left, sr = xpr.right;
if ((sr == null || !sr.red) &&
(sl == null || !sl.red)) {
// 若sr节点为空或者sr节点是黑色的，且sl节点为空或者sl节点是黑色的
// 将xpr节点变成红色
xpr.red = true;
// 则将x节点指向xp节点向上调整
x = xp;
}
else {
//sr和sl中存在一个红节点
if (sr == null || !sr.red) {
//此处说明sl是红节点,将sl节点设置为黑色
if (sl != null)
sl.red = false;
//将xpr节点设置为红色
xpr.red = true;
//右旋
root = rotateRight(root, xpr);
//将xpr节点重新指向xp节点的右节点
xpr = (xp = x.parent) == null ?
null : xp.right;
}
if (xpr != null) {
//如果xpr节点不为空,让xpr节点与xp节点同色
xpr.red = (xp == null) ? false : xp.red;
//当sr节点不为空，变成黑色
if ((sr = xpr.right) != null)
sr.red = false;
}
//存在xp节点
if (xp != null) {
//将xp节点设置为黑色
xp.red = false;
//进行左旋
root = rotateLeft(root, xp);
}
//将x节点指向root进行下一次循环时跳出
x = root;
}
}
}
else { // symmetric
//当x节点是右节点
if (xpl != null && xpl.red) {
//当xpl节点存在且为红色
//将xpl变为黑色，xp变为红色
xpl.red = false;
xp.red = true;
//右旋
root = rotateRight(root, xp);
//将xpl节点重新指向xp节点的左节点
xpl = (xp = x.parent) == null ? null : xp.left;
}
if (xpl == null)
//如果xpl节点不存在，则xp节点没有子节点了
//将x节点指向xp节点向上调整
x = xp;
else {
//sl xpl节点的左节点
//sr xpl节点的右节点
TreeNode<K,V> sl = xpl.left, sr = xpl.right;
if ((sl == null || !sl.red) &&
(sr == null || !sr.red)) {
//若sr节点为空或者sr节点是黑色的，且sl节点为空或者sl节点是黑色的
//将xpl节点变成红色
xpl.red = true;
//则将x节点指向xp节点向上调整
x = xp;
}
else {
//sr和sl中存在一个红节点
if (sl == null || !sl.red) {
//此处说明sr是红节点,将sr节点设置为黑色
if (sr != null)
sr.red = false;
//将xpr节点设置为红色
xpl.red = true;
//左旋
root = rotateLeft(root, xpl);
//将xpl节点重新指向xp节点的左节点
xpl = (xp = x.parent) == null ?
null : xp.left;
}
//如果xpl节点存在
if (xpl != null) {
//使xpl节点与xp节点同色
xpl.red = (xp == null) ? false : xp.red;
//如果sl节点存在
if ((sl = xpl.left) != null)
//将sl节点变为黑色
sl.red = false;
}
// 如果xp节点存在
if (xp != null) {
// 将xp节点设置为黑色
xp.red = false;
// 右旋
root = rotateRight(root, xp);
}
// 将x节点指向root进行下一次循环时跳出
x = root;
}
}
}
}
}
复制代码线程安全
HashMap 不是线程安全的集合， 如果要使用线程安全的 k-v 集合可以使用 CurrentHashMap.
注意事项
使用 Map 的方法 keySet()/values()/entrySet()返回集合对象时，不可以对其进行添加元素操作，否则会抛出 UnsupportedOperationException 异常。
集合初始化时，指定集合初始值大小解释：HashMap 使用 HashMap(int initialCapacity) 初始化，如果暂时无法确定集合大小，那么指定默认值（16）即可。initialCapacity = (需要存储的元素个数 / 负载因子) + 1。注意负载因子（即 loader factor）默认为 0.75，如果暂时无法确定初始值大小，请设置为 16（即默认值）举例：HashMap 需要放置 1024 个元素，由于没有设置容量初始大小，随着元素增加而被迫不断扩容， resize()方法总共会调用 8 次，反复重建哈希表和数据迁移。当放置的集合元素个数达千万级时会影响程序性能。
使用 entrySet 遍历 Map 类集合 KV，而不是 keySet 方式进行遍历。说明：keySet 其实是遍历了 2 次，一次是转为 Iterator 对象，另一次是从 hashMap 中取出 key 所对应的value。而 entrySet 只是遍历了一次就把 key 和 value 都放到了 entry 中，效率更高。如果是 JDK8，使用Map.forEach 方法。values()返回的是 V 值集合，是一个 list 集合对象；keySet()返回的是 K 值集合，是一个 Set 集合对象；entrySet()返回的是 K-V 值组合集合。
Map 类集合 K/V 能不能存储 null 值的情况，如下表格：
| **集合类 ** | Key | Value | Super | 说明 |
|---|---|---|---|---|
| hashtable | 不允许为 null | 不允许为 null | Dictionary | 线程安全 |
| ConcurrentHashMap | 不允许为 null | 不允许为 null | AbstractMap | 锁分段技术（JDK8: CAS） |
| TreeMap | 不允许为 null | 允许为 null | AbstractMap | 线程不安全 |
| HashMap | 允许为 null | 允许为 null | AbstractMap | 线程不安全 |
由于 HashMap 的干扰，很多人认为 ConcurrentHashMap 是可以置入 null 值，而事实上，存储null 值时会抛出 NPE 异常
本文总结
本文主要是说了 hashmap 的初始化过程，以及 hashcode 的计算方式。对于红黑树转化这部分只代码做了一些简单的代码翻译。
对于 hashmap 红黑树这块逻辑由于涉及到数据结构，以后再希望有时间在做一篇文章单独描述。
对于 hashmap 拓容，以及红黑树转链表部分也会在后面的更新中补充。
参考资料
www.zhihu.com/question/20…
www.jianshu.com/p/2c7a4a4e1…
blog.csdn.net/weixin_4234…
作者：老郑_
链接：https://juejin.cn/post/6996999840743817224
来源：掘金
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
评论