【图解算法】螺旋矩阵、旋转矩阵、“之”型输出、矩阵找数
这几道矩阵相关的题目比较考察全局观，如果陷在思考局部点如何移动，那么在面试中将很难快速解出题目。
问题描述
转圈打印矩阵。【leetcode-54-螺旋矩阵】
旋转正方形矩阵。【leetcode-48-旋转图像】
“之”字型打印矩阵。
在行列都排好序的矩阵中找数。【特定的数据】
转圈打印矩阵
【题目】 给定一个整型矩阵Matrix，请按照顺时针转圈的方式打印它。例如:
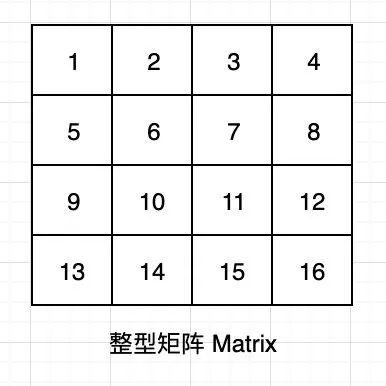实际上存储结构为二维数组打印结果为：
1，2，3，4，8，12，16，15，14，13，9， 5，6，7，11，10
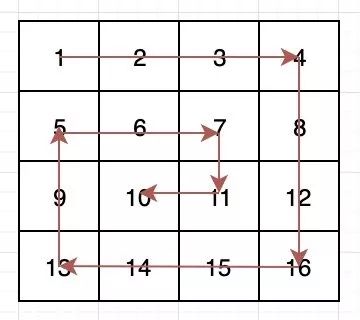转圈打印【要求】 额外空间复杂度为O(1)。
【解法说明】
如果我们将眼光局限于坐标每次该如何移动，如何判断矩阵中哪些点已经输出，哪些点还没有输出，那么你就是进坑里了，这种方法不是不行，但是在面试的场景下，扣各种边界会导致你非常容易出错。那么有什么办法可以快速解决呢？其实很简单，从全局来看，我们实际上是在绘制一个又一个的矩形边界：
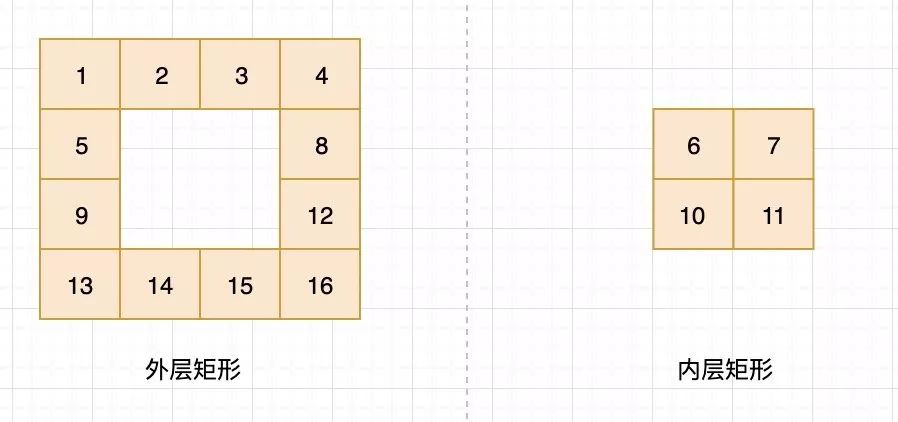将问题转化为绘制矩形边界是不是觉得问题一下子简单了很多，我们只要分别打印四个边界，就能打印出一个矩形；接下来我们考虑外层和内层如何衔接：
如下图所示，我们每次绘制某一边界时（如矩形的上边界），不要把最后一个点绘制了，而是作为下一个边界的起点，那么最终结束位置在5，与下一圈的6正好衔接：
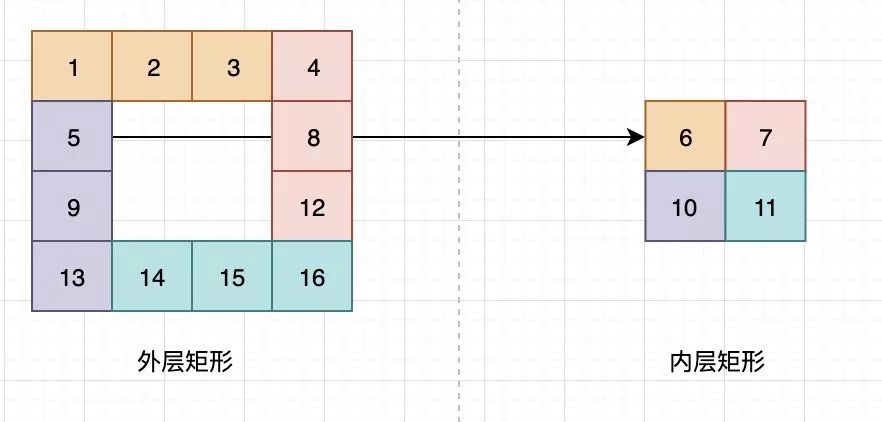内外层衔接看到这里大家想必已经知道怎么做了，是的，我们只需控制左上角和右下角两个点的坐标，然后每跑完一圈，坐标进行相应的增加或减少即可：
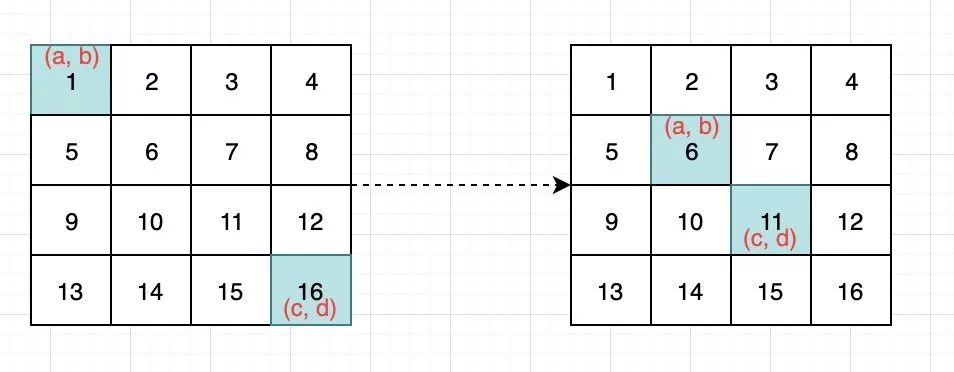控制对角坐标到这里，思路已经基本出现了，我们在外层写一个循环控制对角坐标的变化，内部则是打印一个矩形的外边界的函数：
void circlePrint(vector<vector<int>> &matrix) {
if (matrix.empty()) return; // 空数组判断
int a = 0, b = 0, c = matrix.size() - 1, d = matrix[0].size() - 1;
while (a <= c && b <= d) {
edgePrint(a++, b++, c--, d--, matrix); // 打印(a,b)和(c,d)所在的矩形边界
}
}
关于打印矩形边界，还需要考虑两种边界情况：
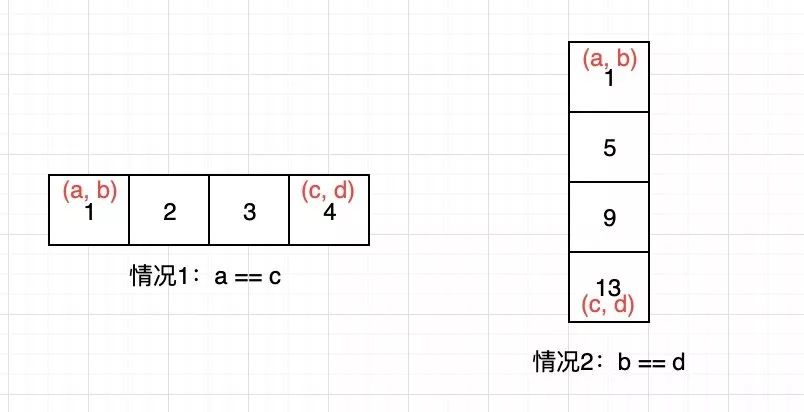打印矩阵的边界考虑至此，我们就可以很轻松地写出代码了：
void edgePrint(int a, int b, int c, int d, vector<vector<int>> &matrix) {
if (a == c) { // only one row
for (int j = b; j <= d; ++j) {
cout << matrix[a][j] << " ";
}
} else if (b == d) { // only one column
for (int i = a; i <= c; ++i) {
cout << matrix[i][d] << " ";
}
} else {
for (int j = b; j < d; ++j) { // print up edge
cout << matrix[a][j] << " ";
}
for (int i = a; i < c; ++i) { // print right edge
cout << matrix[i][d] << " ";
}
for (int j = d; j > b; --j) { // print down edge
cout << matrix[c][j] << " ";
}
for (int i = c; i > a; --i) { // print left edge
cout << matrix[i][b] << " ";
}
}
}
旋转正方形矩阵
【题目】 给定一个整型正方形矩阵 Matrix，请把该矩阵调整成顺时针旋转90度的样子。
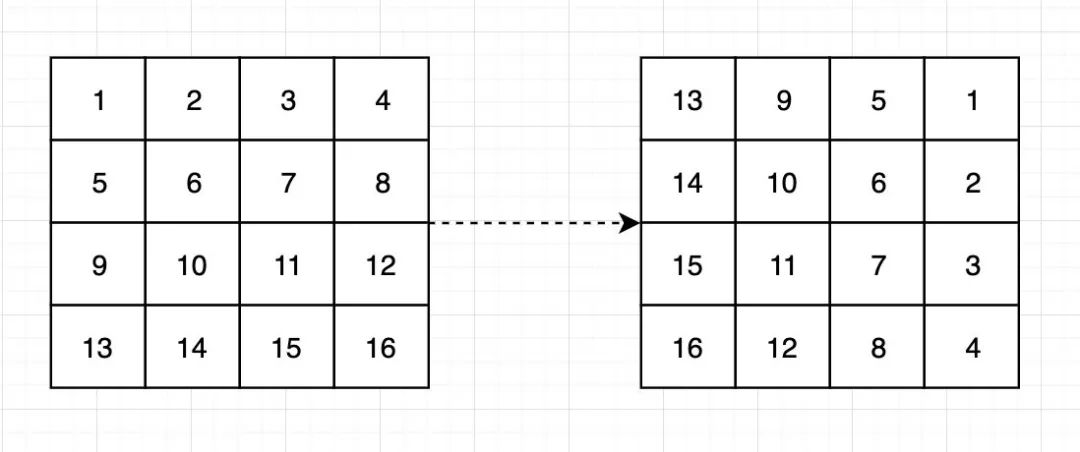原地顺时针旋转90度【要求】 额外空间复杂度为O(1)。
【解法说明】注意到题目要求我们的空间复杂度为O(1)，因此，我们不能借助辅助矩阵，只能原地调整。咋一看好像无从下手，但只要使用我们前面提到过的全局思想，我们可以首先将问题拆解为将一个矩形边界旋转90度：
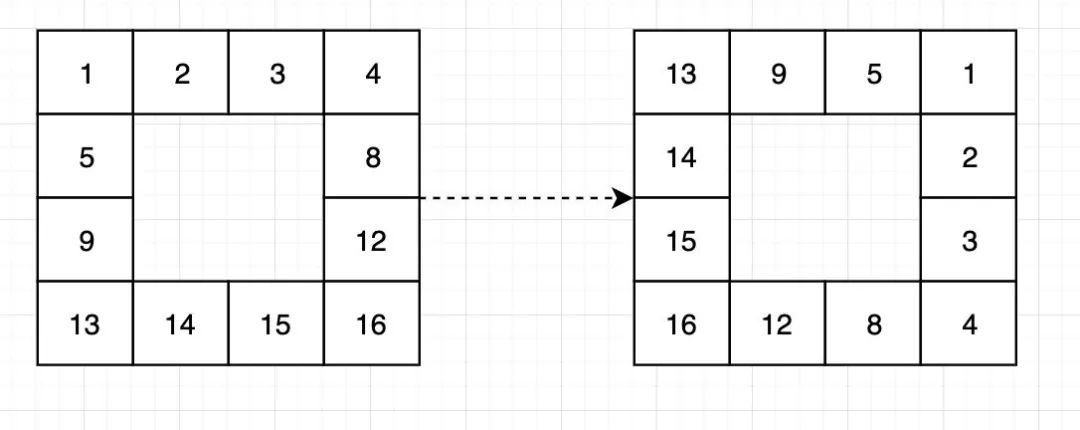化简为边界旋转的问题代码如下：
void rotateMatrix(vector<vector<int>> &matrix) {
int a = 0, b = 0, c = matrix.size() - 1, d = matrix[0].size() - 1;
while (a <= c && b <= d) {
rotateEdge(a++, b++, c--, d--, matrix); // 旋转指定对角所在正方形的边界
}
}
接下来，我们要解决的就是如何将一个矩形边界旋转的问题了。
我们先考虑四个角：
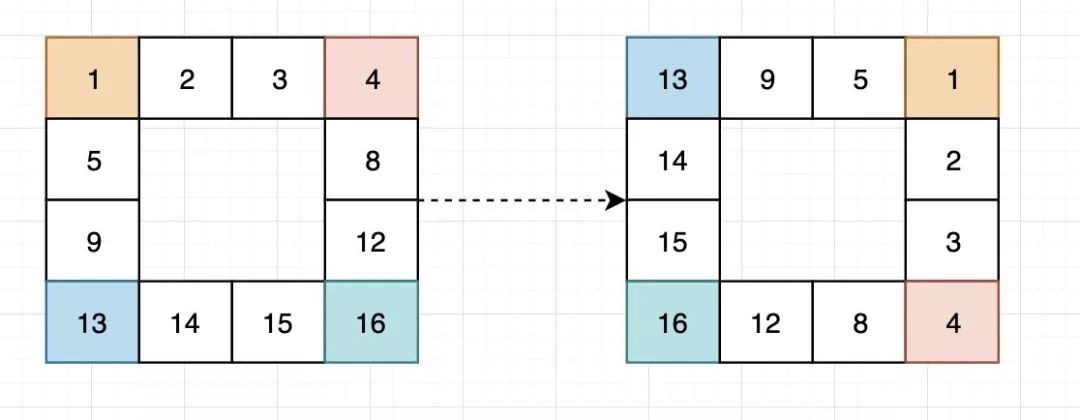边界旋转的四个角再考虑第二个点：
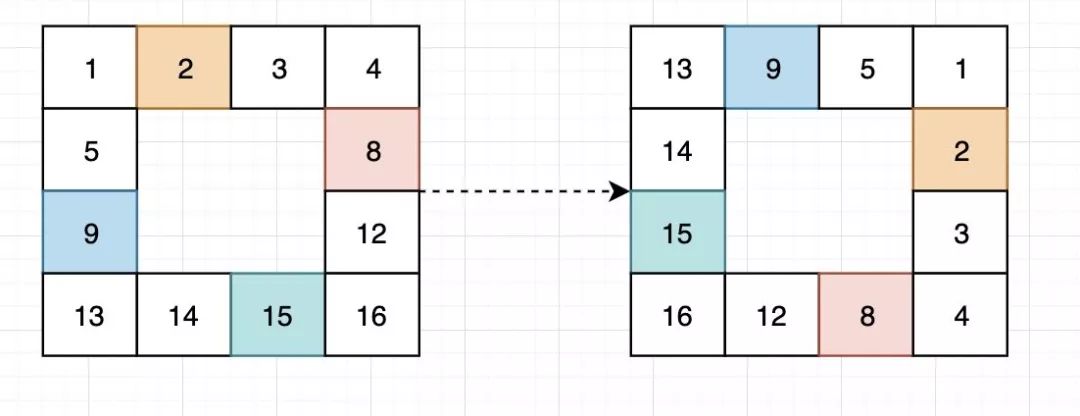旋转边界的第二个点聪明的朋友可能已经发现了，这个跟遍历某一个边界的一边非常像，我们原地交换四个点只需要5步，再加上遍历某一边，旋转一个边界就此完成。
代码如下：
void rotateEdge(int a, int b, int c, int d, vector<vector<int>> &matrix) {
for (int i = 0; i < d-b; ++i) { // 每一行要剔除最后一个点
int temp = matrix[a][b + i]; // 暂存左上角的点
matrix[a][b + i] = matrix[c - i][b]; // 把左下角的点放到左上角
matrix[c - i][b] = matrix[c][d - i]; // 把右下角的点放到左下角
matrix[c][d - i] = matrix[a + i][d]; // 把右上角的点放到右下角
matrix[a + i][d] = temp; // 把暂存的左上角的点放到右上角
}
}
“之”字型打印矩阵
【题目】 给定一个矩阵matrix，按照“之”字形的方式打印这 个矩阵，例如:
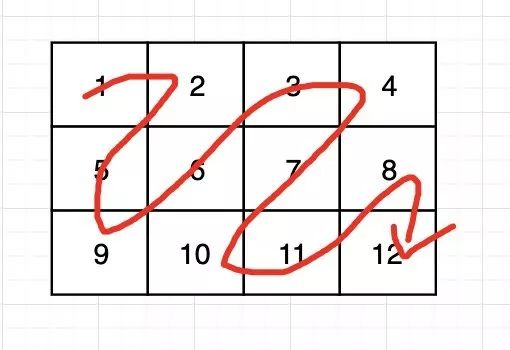“之”字型打印“之”字形打印的结果为：
1，2，5，9，6，3，4，7，10，11， 8，12
【要求】 额外空间复杂度为O(1)。
【解法说明】和之前的题目类似，一旦我们陷于考虑局部的坐标如何变换，就会陷入细节边界之中，难以快速解决这道题目。我们换个思路，将整个过程切分为：给定两个对角点坐标，遍历对角线，然后寻找两个对角点坐标的变化规律。
给定两个对焦点坐标，遍历该对角线，实现起来非常简单：
void printDiagonal(int a, int b, int c, int d, vector<vector<int>> &matrix) {
while (a >= c && b <= d) { // 从左下到右上的遍历方式
cout << matrix[a--][b++] << " ";
}
}
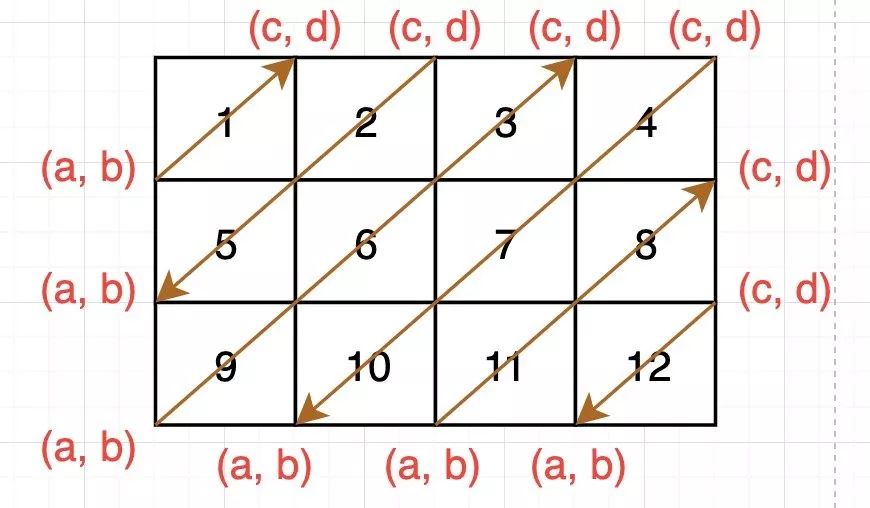遍历对角线图中的(a, b)为对角线的左下角顶点，其中a、b均是变量，从左到右分别为每次变换的位置；一开始(a, b)和(c, d)都是点1，即matrix[0][0]；我们观察两个点的变换轨迹，可以发现，(a, b)先向下走，到底部再向右走；而(c, d)先向右走，到达最右边才向下走。
与此同时，每完成一次对角线遍历，我们发现，遍历的方向会发生改变，因此我们使用一个bool类型的isUp来记录状态。
因此，对角线函数需要进行修改：
void printDiagonal(int a, int b, int c, int d, vector<vector<int>> &matrix, bool isUp) {
if (isUp) {
while (a >= c && b <= d) {
cout << matrix[a--][b++] << " ";
}
} else {
while (a >= c && b <= d) {
cout << matrix[c++][d--] << " ";
}
}
}
遍历所有对角线：
void ZigZagPrint(vector<vector<int>> &matrix) {
bool isUp = true;
int a = 0, b = 0, c = 0, d = 0;
while (c != matrix.size()) { // c 如果为 n，说明右上角的对角线顶点已经到达矩阵的右下角，所有对角线都被遍历了
printDiagonal(a, b, c, d, matrix, isUp);
isUp = !isUp;
b = (a == matrix.size() - 1) ? b + 1 : b; // 注意，我们要先更新b，然后才更新a
a = (a == matrix.size() - 1) ? a : a + 1;
c = (d == matrix[0].size() - 1) ? c + 1 : c; //同样的，先更新c，再更新d
d = (d == matrix[0].size() - 1) ? d : d + 1;
}
}
在行列都排好序的矩阵中找数
【题目】 给定一个有N*M的整型矩阵Matrix和一个整数K， Matrix的每一行和每一 列都是排好序的。实现一个函数，判断K 是否在 Matrix中。例如：
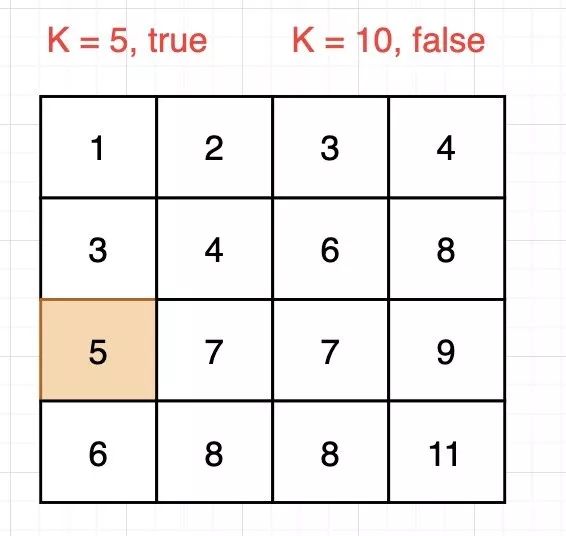从排好序的矩阵中找数如果K为5，返回true；如果K为10，返回false。
【要求】 时间复杂度为O(N+M)，额外空间复杂度为O(1)。
【解法说明】如果我们遍历完整个矩阵，需要O(N^2)，而题目中要求O(N+M)的复杂度，因此我们就需要根据特殊的数据布局来考虑更优的解法。懂得二分法的朋友肯定知道，我们在一个排好序的数组中找一个数，从中间找起是最快的；这里也是类似，不过这里的中间在哪里呢？
事实上，考虑数据的分布，左上角必然是最小值，右下角必然是最大值，而中间线，正好在左下角到右上角的对角线上：
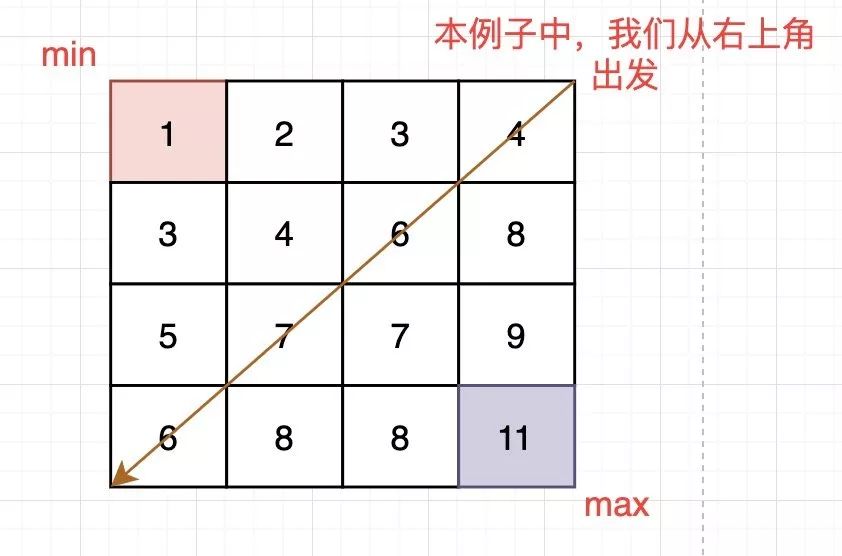从中间线出发假设我们找K=5，从右上角开始，发现4 < 5，所以向下找，为什么？因为行列都是按顺序排好的，4左边的数都是比4小的，既然5比4大，那么在左边就不可能找到5了：
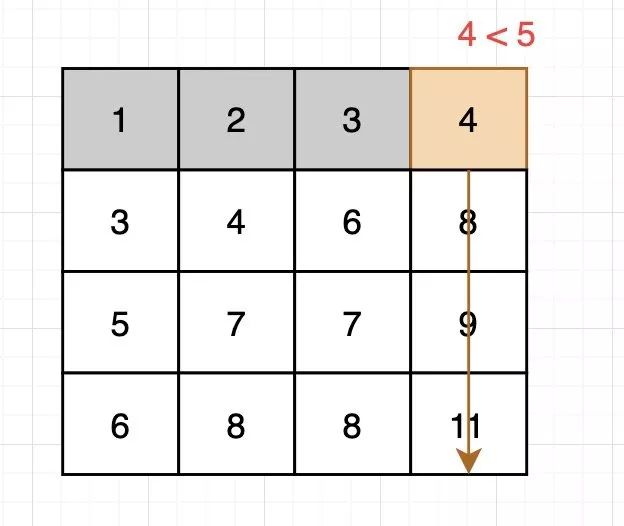4的左边已经不存在5了接下来我们继续比较，发现8 > 5，所以向左找，因为下面不可能有5了：
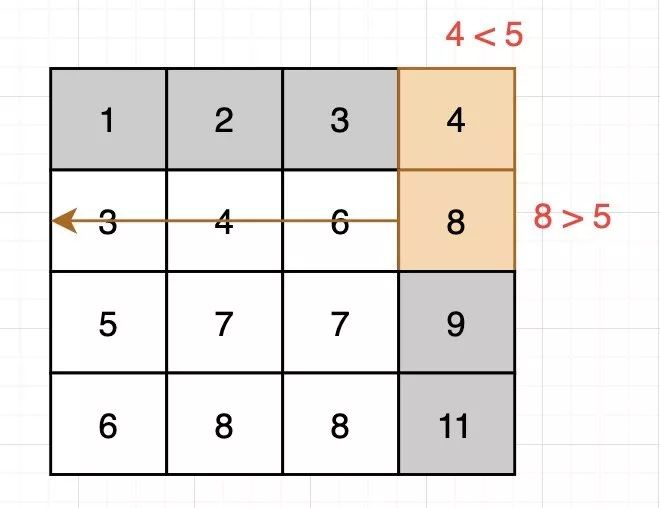8的下面不可能存在5按照上面的方式，我们完成搜索：
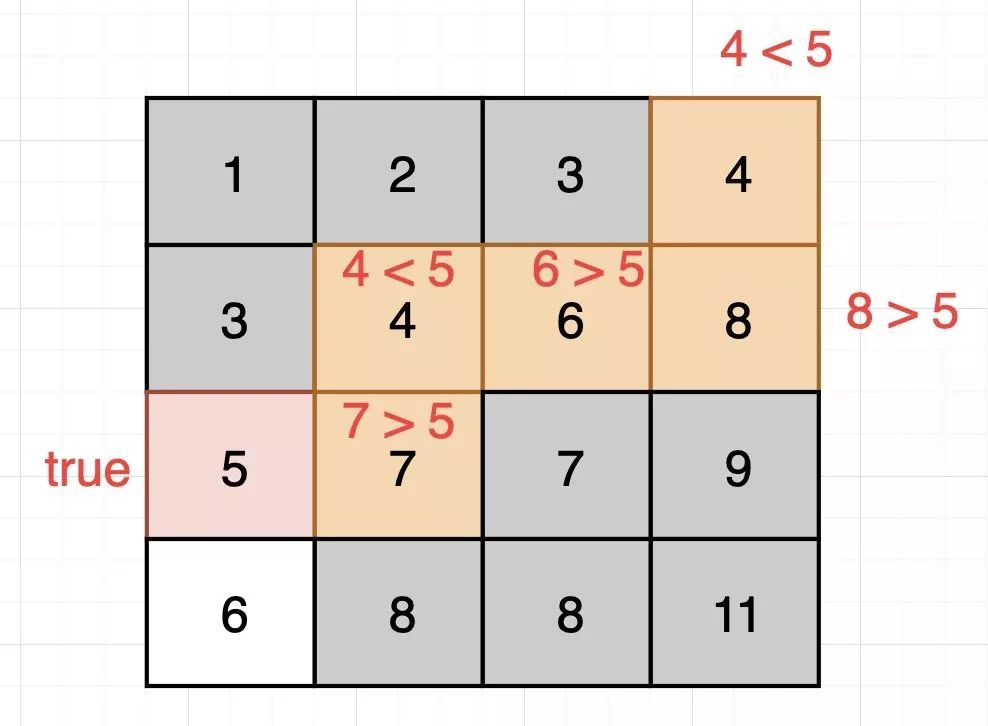找到5，返回true我们仔细考虑下过程，即使K在左下角，我们从右上角开始找，那么最终耗费的时间也只是O(N+M)，N 为宽度，M 为长度。
代码实现：
bool findKInSortedMatrix(vector<vector<int>> &matrix, int k) {
int a = 0, b = matrix[0].size() - 1;
while (a <= matrix.size() - 1 && b >= 0) {
if (matrix[a][b] == k) { // found
return true;
} else if (matrix[a][b] < k) { // 如果当前点小于 K，向下走
a++;
} else { // 如果当前点大于 K，向左走
b--;
}
}
return false; // not found
}
其他算法推荐：二分法
1、二分法题型小结
2、两道看似简单的面试高频算法题
3、如何理解二分查找？生活中还能用来设计骗局？
4、二分搜索只能用来查找元素吗？
推荐阅读
【吐血整理】百度云珍藏了四年书籍+临时搜索，帅地给大家整理了几百本常用电子书(附下载链接)！！