带通采样定理及基于Simulink的应用仿真
0 前言
香农采样定理,又称奈奎斯特采样定理或低通采样定理,是通信与信号处理学科中的一个基本结论。
Nyquist采样定理描述如下:
假设有一个频带受限的信号x(t),其频带被限制在(0,fH)以内,如果以不小于fs=2fH的采样率对该信号进行采样,并且得到时间离散的采样信号x(n)=x(nTs)(其中Ts=1/fs,为采样时间间隔),则原信号x(t)可以由采样序列x(n)完全确定。若x(t)是带宽非受限的,则需要在采样前先利用抗混叠滤波器对x(t)进行滤波,滤除f≥fH的高频成份。
Nyquist采样定理讨论的是频谱分布在(0,fH)上的基带信号的采样问题,然而对于某些带通信号,例如雷达接收机的接收信号大多为调制的射频信号,射频信号的频率上限远高于基带信号的频率上限,但是频率却分布在有限的(fL,fH)范围内。虽然可以按高于最高频率的2倍进行Nyquist采样,但是当最高频率远远大于信号带宽B时,如果按照Nyquist采样率进行采样,则其采样率会非常高,现实中的AD采集芯片要么难以实现如此高的采样率,要么采样部分的成本巨大,这时候Nyquist采样定理已经不能满足实际中的使用要求,在这种情况下,带通采样便发挥了应有的作用。
1 概述
我们首先介绍带通采样定理,其次以外差干涉信号的解调为例,借助MATLAB的Simulink工具描述带通采样定理的实际应用。
2 带通采样定理[1]
带通采样定理推导如下:
假设连续信号xa(t)带宽为B,中心频率为fc,频带限制在(fL,fH)内,原始信号表示为如下形式(公式1):
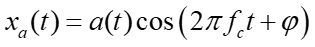
其中a(t)表示信号的幅值,φ表示相位。令采样频率为fs,经过采样以后得到的离散信号表示为(公式2):
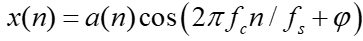
对其做离散傅里叶变换,转化为频域表示为(公式3):
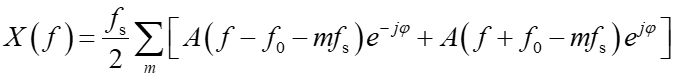
从上式可以看出,带通信号经过采样后,频谱图形表现为在原始频谱的基础上以采样频率为周期向左右两侧进行周期性拓展。假设原始信号的频谱图形如图1(a)所示,则经过采样率fs的采样后频谱为图1(b)所示:
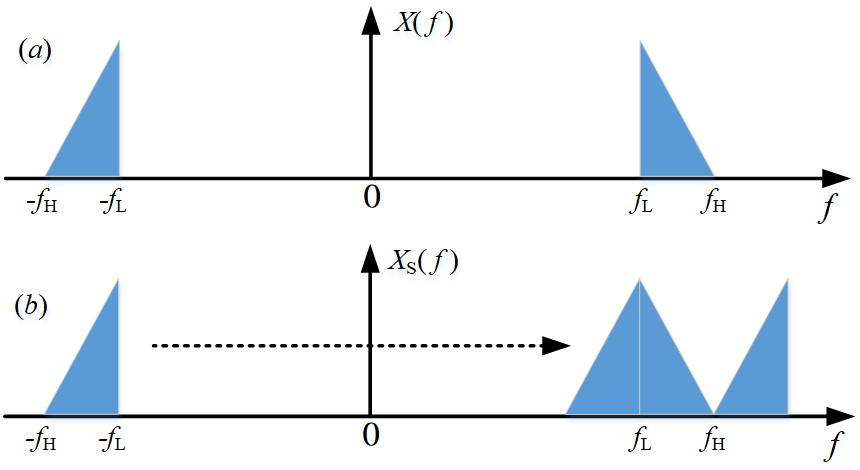
图1:带通信号采样前后频域变化图
由上图可以看出,为使采样后的频域不发生混叠,需要使信号负频域的分量经过m-1和m次平移后得到的频谱曲线不能与信号原本的正频域分量重叠,因此必须满足以下不等式(公式4):
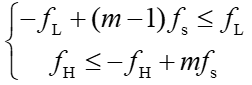
由(4)式进行变换,可得(公式5):
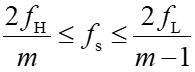
在整个推导过程中m是整数,因此m取值需要满足如下要求(公式6):
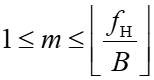
其中⌊*⌋表示向下取整。
从上面的结论可以看出,当m=1时,正好是Nyquist采样。对于带通信号,不必要使采样频率高于信号频率上限的2倍,若采样频率为信号带宽的整数倍时,只需大于信号带宽的2倍即可。在一些文献中,带通采样定理也有另一种表述方式(公式7):
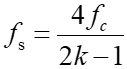
其中,fc为被采样信号的中心频率,k可以取任意能够使fs≥2B的正整数,它表示被采样的中频信号在当前采样频率的第k个Nyquist区域。下面对这样的结论进行推导。
将原始信号用如下方式表示(公式8):
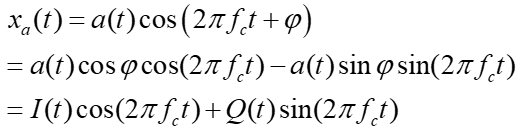
其中I(t)=a(t)cos(φ)、Q(t)=a(t)sin(φ),分别表示基带信号的同相分量和正交分量。令Ts表示采样周期,则采样后的信号表示为(公式9):
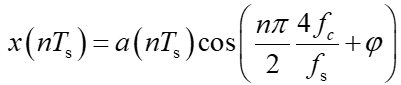
若4fc/fs为奇数,即4fc/fs=2k-1,其中k=1,2,3...),当n为偶数时有(公式10):
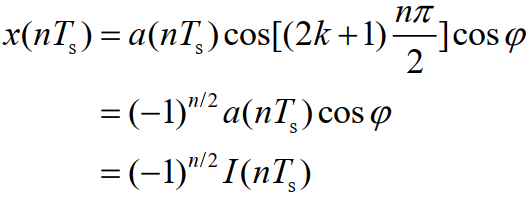
当n为奇数时有(公式11):
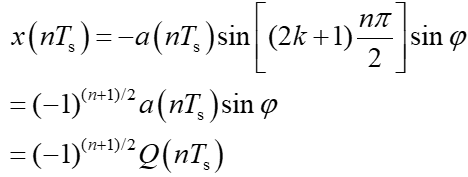
从式(10)和式(11)中可以看出,若4fc/fs为奇数,则采样后信号表现为I、Q两路以奇偶的形式交替出现。如果对其采用合理的插值滤波算法,校正采样后两路在时域上的延迟,就可以恢复出完整的I、Q两路信号。由此可见,使4fc/fs为奇数是可行的。当采样率为fs时,第k个Nyquist区域是[(k-1)fs/2,kfs/2],而信号的中心频率为fc=(2k-1)fs/4,刚好是Nyquist的中间位置。所以第二种带通采样的表达方式使被采样的信号的中心频谱刚好落到Nyquist区域的中心位置,可以最大限度的保证采样后的频谱不发生混叠。也就是说,带通采样定理的式(7)的表达方式是式(5)的一种最佳的特殊情况,所以得到广泛使用。
3 基于MATLAB Simulink的仿真验证
这部分以外差干涉信号解调为例来简要说明带通采样定理的具体应用。假设待解调的外差干涉信号时域表达式如下(公式12):
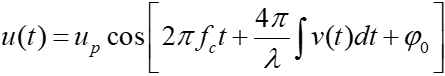
其中有(公式13):
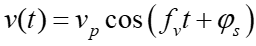
式(12)与(13)中,up,fc,φ0分别为u(t)的峰值、载波频率及初相。λ为激光波长;vp与fv及φv分别为激励速度v(t)的峰值与频率及初相。
不妨令fc=40 MHz,φ0=0,up=32767(即2^15-1),vp=0.6(即峰峰值为1.2),fv=400 kHz,φv=0,λ=632.8 nm(氦氖激光器波长)。
取以上参数时,在Nyquist采样条件下(采样率为250 MSPS时)的外差信号频域结果如下图所示(局部放大):
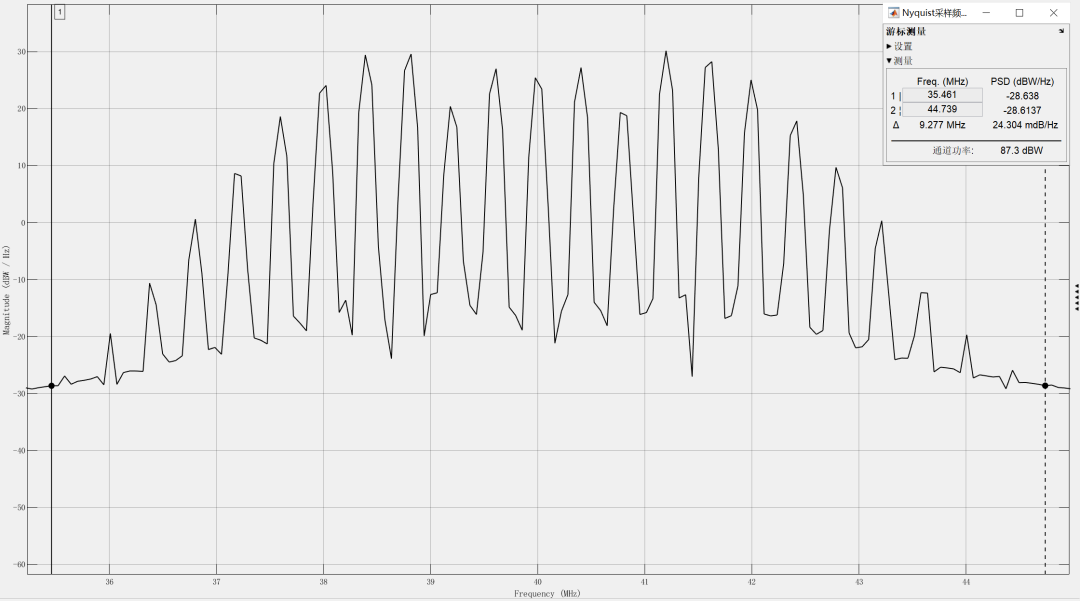
图2:Nyquist采样条件下的外差信号频域结果
由图2可知,上述外差干涉信号属于带通信号,因此可在较低采样率下对信号进行带通采样。根据图2可以保守地估计信号的频率范围为(35 MHz,45 MHz),根据前文的带通采样推导,可以取m=4,此时带通采样的最佳采样率范围为:22.5 MSPS≤fs≤23.3 MSPS,不妨取fs=22.8 MSPS,此时可得到采样后的信号频域结果如下:
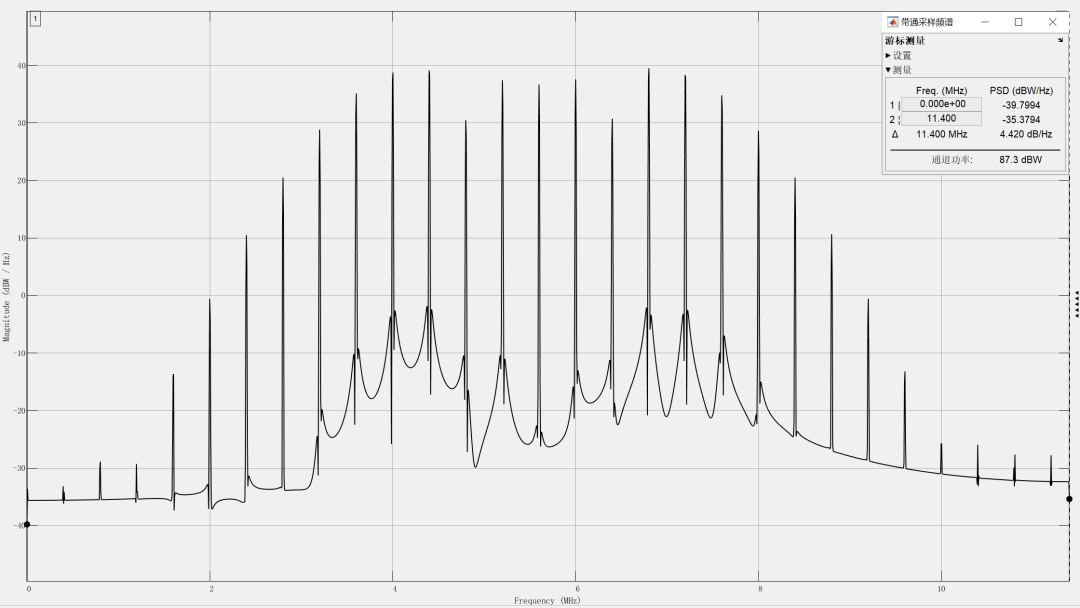
图3:带通采样条件下的外差信号频域结果
上图可知,原来中心频率为40 MHz的信号经过带通采样后,中心频率变成了5.6 MHz。在此条件下对外差干涉信号进行解调,解调程序如下图所示:
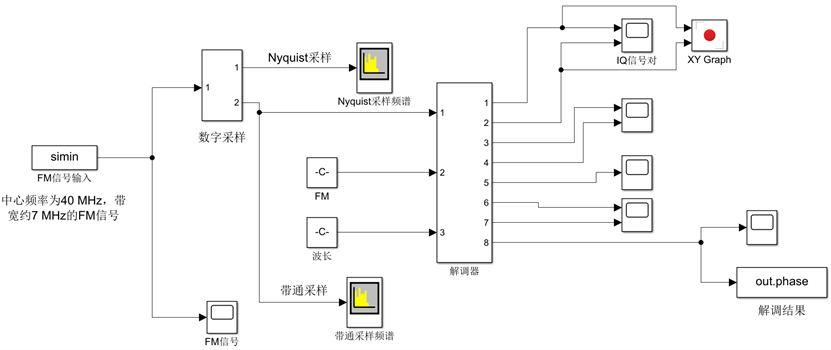
图4:解调程序
最终的解调结果(频域和时域)如下所示:
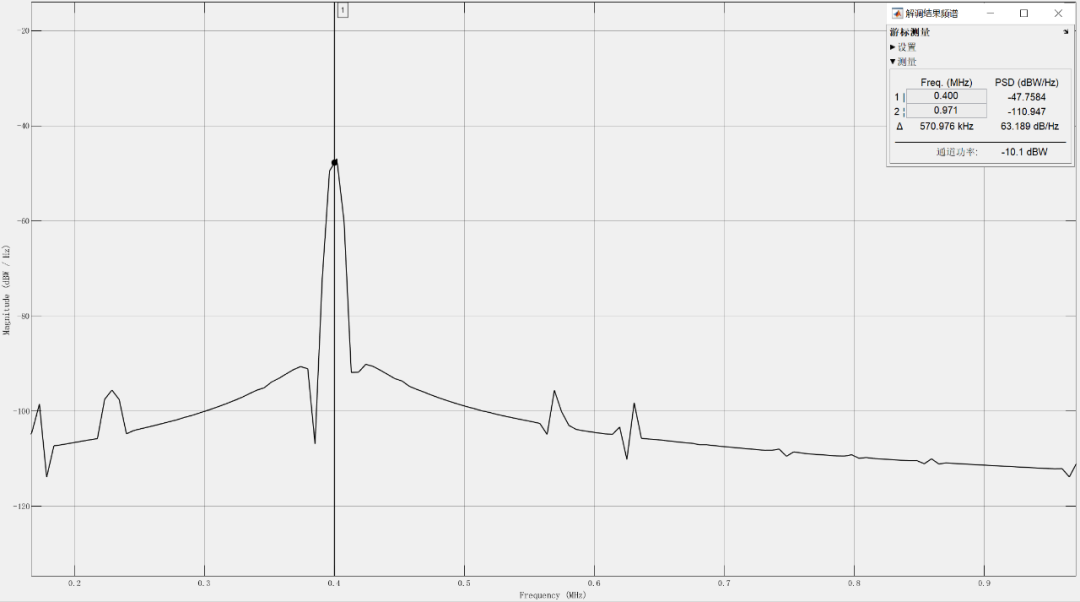
图5(a) 解调结果频域图
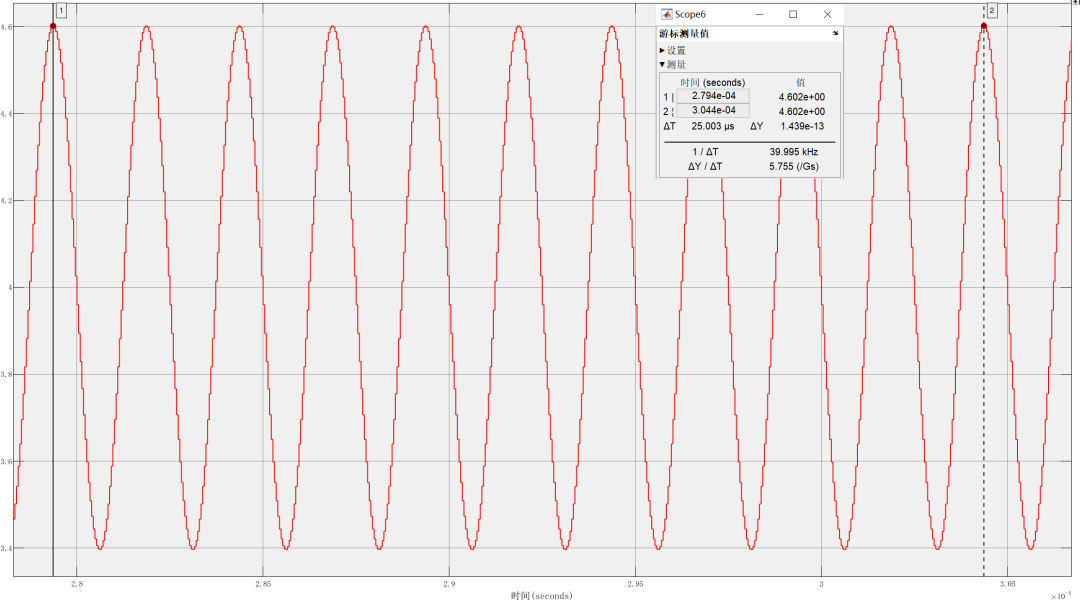
图5(b) 解调结果时域图
图5解调结果为:波形频率约为400kHz,峰峰值为1.2(后续还可以对解调完成的信号进行内插滤波)。上述解调结果与设定值一致,这表明在带通采样条件下正确地恢复了原始相位信息。
4 结论
本文简要地介绍了带通采样定理,并以外差干涉信号的频率解调为例,借助MATLAB的Simulink工具实现了在带通采样条件下对外差干涉信号的解调。上述解调结果表明,在满足带通采样条件时,使用带通采样可以在极大地降低采样率的情况下正确地恢复出原始相位信息。
5 参考文献
[1] 张诚. 宽带复杂雷达信号合成技术研究[D].西安电子科技大学,2014.

长按识别二维码关注我们
微信号 :RPIBMEPhD

微信号|RPIBMEPhD



写在后面
这是一群致力于科研传播的faculty & PhD记录分享点滴思考的平台,这里有我们在各自领域(机器学习,医疗影像,材料科学,凝聚态物理,生物信息,光学成像等)涉猎研究的点滴感悟,有我们在国内,海外求学工作奋斗的酸甜苦辣,亦有偶尔的风月和我们的诗与远方。
——纯真学者团队




