基于图形剪切的图像分割
点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达
图像分割技术是计算机视觉领域的一个重要研究方向,也是图像语义理解的重要组成部分。图像分割是指将图像分割为具有相似属性的几个区域的过程。从数学的角度来看,图像分割是将图像分割成不相交区域的过程。该区域可以是图像的前景和背景,也可以是单个对象。可以使用颜色、边缘或邻域的相似性等要素构造这些区域。
图形切割算法是组合图形理论的经典算法之一。近年来,许多学者将之应用于图像和视频分割,取得了良好的效果。本文简要介绍了图形切割算法和交互式图像分割技术,以及图形切割算法在交互式图像分割中的应用。
01.基本概念
运用图形理论领域的理论和方法将图像映射到加权无定向图形中,将像素视为节点,将图像分割问题视为图形的顶点分割问题,利用最小的切割标准获得图像的最佳分割。
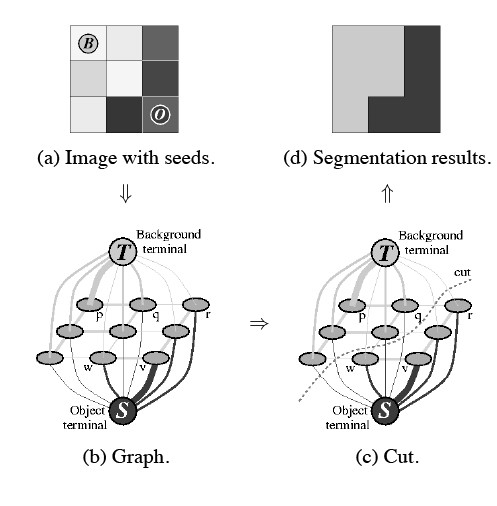
这种方法将图像分割问题与MIN-CUT问题关联在一起。通常的方法是将要分割的图像映射到加权无方向图形 G=(V,E),其中 , V 是顶点集,E 是边集。每个两个相邻顶点的连接形成的边称为 n 链接,每个普通顶点和两个终端顶点之间的连接称为 t 链接。每个节点对应于图像中的每个像素,每个边 ∈ E 连接一对相邻像素,并且边缘的权重为 w(i,j)表示相邻像素之间的灰色、颜色或纹理的非负相似性。
博伊科夫和乔利最初提议计算标记像素的直方图,以近似概率密度函数,并让
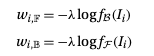
例如,如果 fB 非常低,则 wi,F 将非常高,因此更有可能剪切 i 和 B 之间的边缘。使用简单的相似性度量计算节点间权重
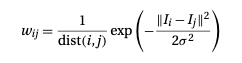
Blake 等人演示了如何σ图像样本的局部对比度来估计参数。
我们以两类除法为例,将G = (V,E) 分成两个子集 A、B 。这两个子集对应于前景像素集和图像的背景像素集,这相当于完成图像分割,其中:
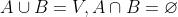
图像的分割 S 是图像的剪切,分割的每个区域 C ∈ S 对应于图像中的子图像。在组合优化中,将切割成本定义为其切断的边缘成本之和是正常的。
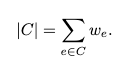
切割的成本是边集 C 中所有边的重量的总和。
02. Maxflow-Mincut 理论
图形中的流
我们考虑一个定向图(S,A),具有一组无限顶点S和一组弧线,连接其中一些顶点。
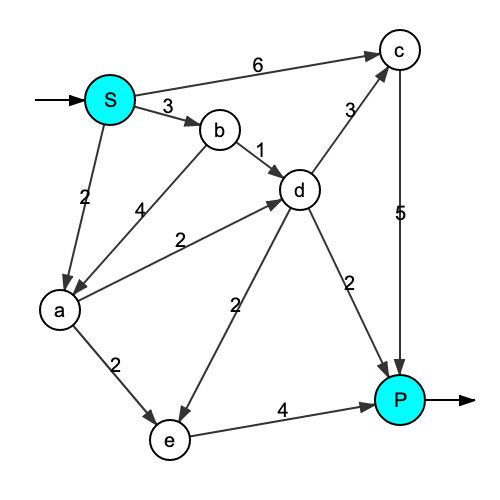
顶点中区分为源S,井P.与每个弧线关联一个严格的正实数,称为电容。
我们寻求通过液体的最大流量,从源头到井——每个弧线中的流量不超过其容量。换句话说,我们正在寻找 R 中一组弧的函数 f,以便:
对于任何弧 a,0≤f (a) ≤ c (a),其中 c (a) 是弧的容量。
对于源或井以外的任何顶点,传入圆弧的流速之和等于传出圆弧的流的总和。
我们谈到这样的应用程序的流程。我们寻求确定最大流量,在意义上
离开源的弧的流速之和为最大值。
下面是一个流的示例。
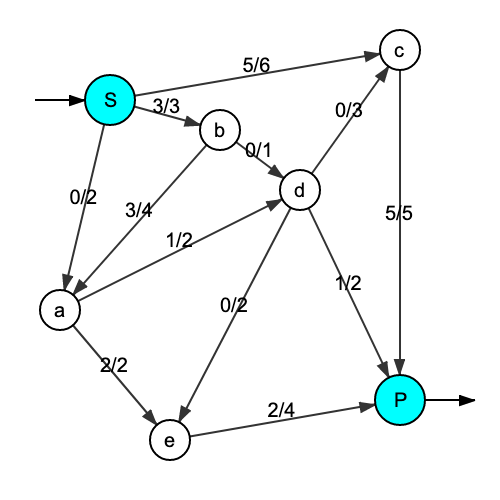
然而,它不是最大值,例如,可以通过在S-a-b-d-e-P路径上添加1的比特率来改进。
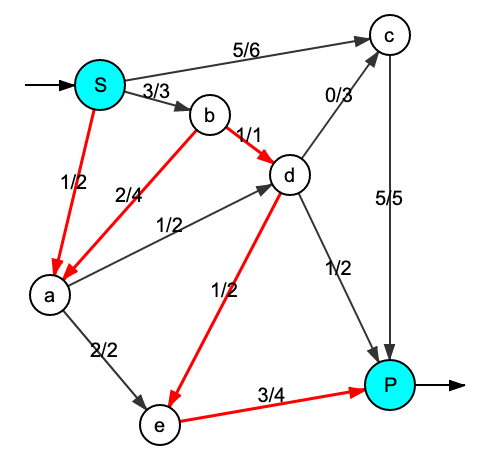
有几种算法可以实现最大流量,例如 Dinic 或 ISAP 算法。
最小切割
最大流量的值等于最小切入的值。
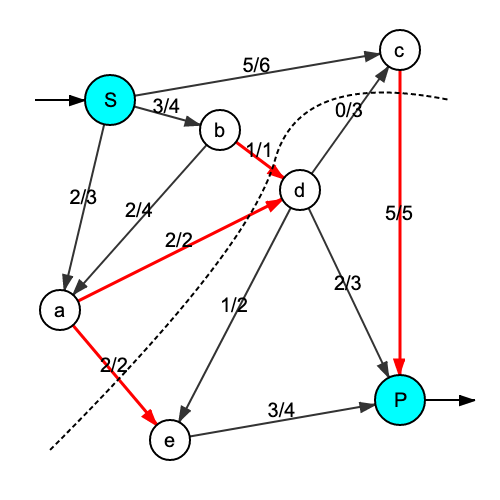
此外,如果 (A, B) 是最小切口,并且 a 是弧线,其起点为 A,结束为 B,则由任何最大流量饱和。
03.结论
本课介绍图像处理的基本低级操作和工具,这些操作和工具是理解大多数常用的计算机视觉方法和工具所必需的。
04,参考文献
1. Yuri Y. Boykov Marie-Pierre Jolly.Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in N-D Images
2. A. Blake, C. Rother, M. Brown, P. Pérez, and P. Torr. Interactive image segmentation usingan adaptive GMMRF model. InEuropean Conference on Computer Vision (ECCV), 2004.
3. Yuri Boykov, Vladimir Kolmogorov: An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision. IEEE Trans. Pattern Anal. Mach. Intell. 26(9): 1124–1137 (2004)
4. Adelson, Edward H., and James R. Bergen (1991), “The plenoptic function and the elements of early vision”, Computational models of visual processing 1.2 (1991).
5. Boykov, Y., Veksler, O., and Zabih, R. (2001), “approximate energy minimization via graph cuts,” IEEE Transactions on Pattern Analysis and Machine Intelligence, 23(11): 1222–1239.
6. D.M. Greig, B.T. Porteous and A.H. Seheult (1989), Exact maximum a posteriori estimation for binary images, Journal of the Royal Statistical Society, Series B, 51, 271–279.
7. D. Geman and S. Geman (1984), Stochastic relaxation, Gibbs distributions and the Bayesian restoration of images, IEEE Trans. Pattern Anal. Mach. Intell., 6, 721–741.
8. J.E. Besag (1986), On the statistical analysis of dirty pictures (with discussion), Journal of the Royal Statistical Society Series B, 48, 259–302.
交流群
欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~
