终于把时间序列分析的关键点全讲清楚了！-轻识

编辑：机器学习研习院

时间序列的定义

一个时间序列过程(time series process)定义为一个随机过程，这是一个按时间排序的随机变量的集合，也就是将每一个时刻位置的点作为一个随机变量。是索引集合(index set)，决定定义时序过程以及产生观测值的一个时间集合。其中假定

随机变量的取值是连续的。
时间索引集合是离散且等距的。

在整个过程中，都采用以下符号

随机变量(Random variables)用大写字母表示，即，同时随机变量的值是从一个分布中采样给出。而且可以为无限多个时间点定义随机变量。
观测(Observations)用小写字母表示，即，观测可以认为是随机变量的实现。但通常在实际中，我们的观测点是有限的，因此定义个观测是。

时间序列分析的目标

给定一组时间序列数据，通常会要求回答一个或多个有关它的问题。时间序列数据出现的主要问题类型取决于数据的上下文以及收集数据的原因，下面给出一些常见的目标：

描述：描述时间序列的主要特征，例如：序列是递增还是递减；是否有季节性模式（例如，夏季较高，冬季较低）；第二个解释变量如何影响时间序列的值？
监控：检测时间序列行为何时发生变化，例如销售额突然下降，或者突然出现峰值。
预测：从当前值预测时间序列的未来值，并量化这些预测中的不确定性，比如根据今天的气温预测未来几天的温度。
回归：给定多个时间序列以及与这些序列对应的一个额外的值，找到其中的关系。
分类：给定多个时间序列，将它们按照相似性进行分类。
......

时间序列的建模

时间序列数据通常被分解为以下三个组成部分。

趋势（Trend）- 趋势体现的是时间序列数据均值随时间的长期变化。如果趋势存在，它的形状通常会引起人们的兴趣，尽管它可能不是线性的。
季节性影响（Seasonal effect）- 季节性影响是时间序列中以固定间隔重复的趋势。严格来说，季节性效应只是每年都会重复的效应，但在更一般的情况下，可以更广泛地使用该术语来表示任何定期重复的模式。
无法解释的变化（Unexplained variation）- 无法解释的变化是在任何趋势和季节性变化被去除后时间序列中其余的变化。这种无法解释的变化可能是独立的，也可能表现出短期相关性。

因此，时间序列数据的简单模型可以用两种方式表示，分别为

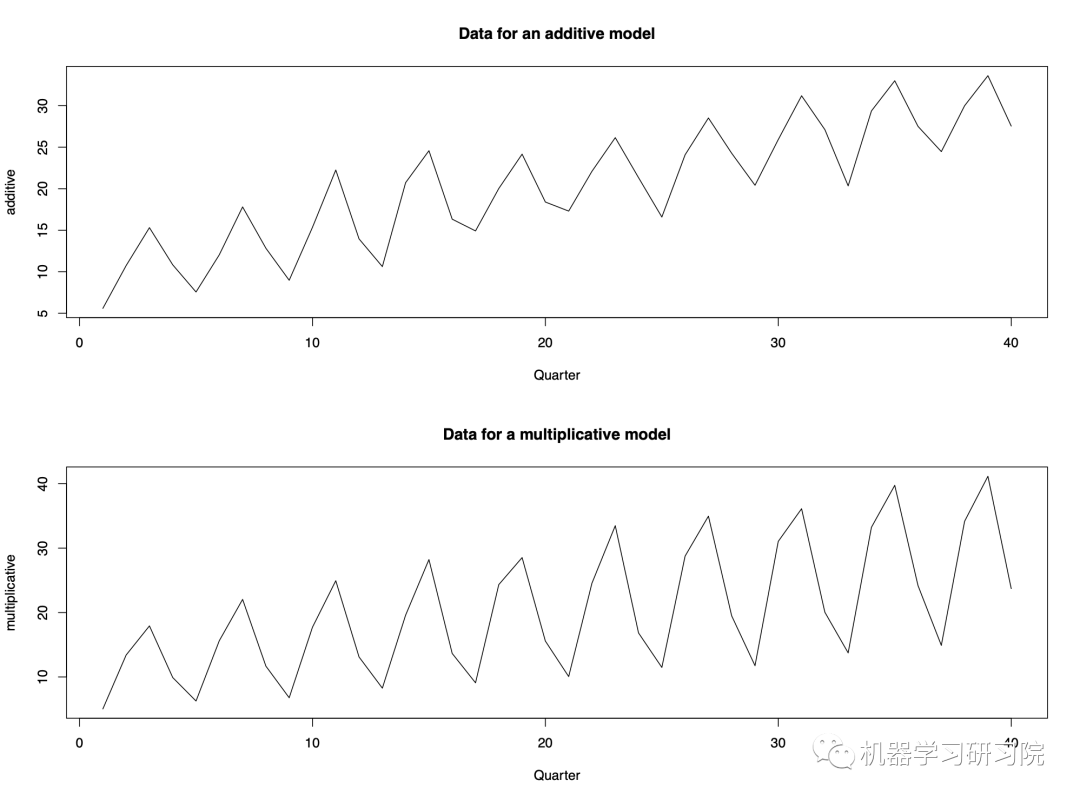
加法模型（Additive）：
乘法模型（Multiplicative）：

其中表示趋势，表示季节，表示无法解释的变化。在此教程中，给出了两个例子。即当趋势和季节性变化独立作用时，加法模型是合适的，而如果季节性效应的大小取决于趋势的大小，则需要乘法模型。当趋势和季节性变化独立作用时，加法模型是合适的，而如果季节性效应的大小取决于趋势的大小，则需要乘法模型，简单的示意图如下：

Example of additive model

时间序列的特性

(均值、方差、自协方差函数、自相关函数)

给定一个时间序列过程和观测，通常我们会使用以下属性描述其特征。

均值(Mean function)

对所有的，时间序列过程的均值函数（mean function）定义为

对于真实的数据，通常我们假定均值为一个常数，因此可以估计均值为

如果数据的平均值不是恒定的，例如由于趋势或季节性变化的存在，则应该用其他方法进行估计，这部分内容后面再讲。

方差(Variance function)

对所有的，时间序列过程的方差函数（variance function）定义为

标准差函数定义为

对于真实的数据，通常我们假定方差也为一个常数，因此可以估计方差为

自协方差和自相关函数(Autocovariance and autocorrelation functions)

回忆对任意的随机变量和，协方差以及相关性测量通过以下定义给出

协方差：

lag=0

在滞后 0 （lag=0）处样本的自协方差函数定义为，它是与之间的协方差。根据上面的公式，计算方式为

因此，滞后 0 处的样本自协方差函数是样本方差。类似地，滞后0处的自相关性为

lag=1

在滞后 1（lag=1）处的样本自协方差函数是时间序列和协方差。它是序列与自身移动一个时间点序列的协方差，根据以上公式，协方差和自相关系数计算方式为

及

其中

是后个观测值；

在实际应用中，通常假设前 n-1 个观测值的均值和方差等于最后 n-1 个观测值的均值和方差，这样可以简化上述表达式。此外，对于协方差公式，使用除数 n 而不是无偏 n-2。显然，当 n 很大时，改变除数对计算几乎没有实际影响。

lag=

时间序列的样本自协方差函数 (ACVF)定义为：

样本自相关函数 (ACF) 定义为

以下链接中找到有助于理解自协方差和自相关函数的交互式示例。

https://shiny.maths-stats.gla.ac.uk/gnapier/Time_Series_ACF/shiny.maths-stats.gla.ac.uk/gnapier/Time_Series_ACF/

Correlogram图的解释

Correlogram讲自相关函数的计算结果作为纵轴，将滞后作为横轴的一种图。可以很直观的看出时间序列不同lag之间的相关性。Correlogram会告诉时间序列分析师很多关于时间序列的信息，包括趋势的存在、季节性变化和短期相关性。这里用一些例子来说明。

Example - purely random data

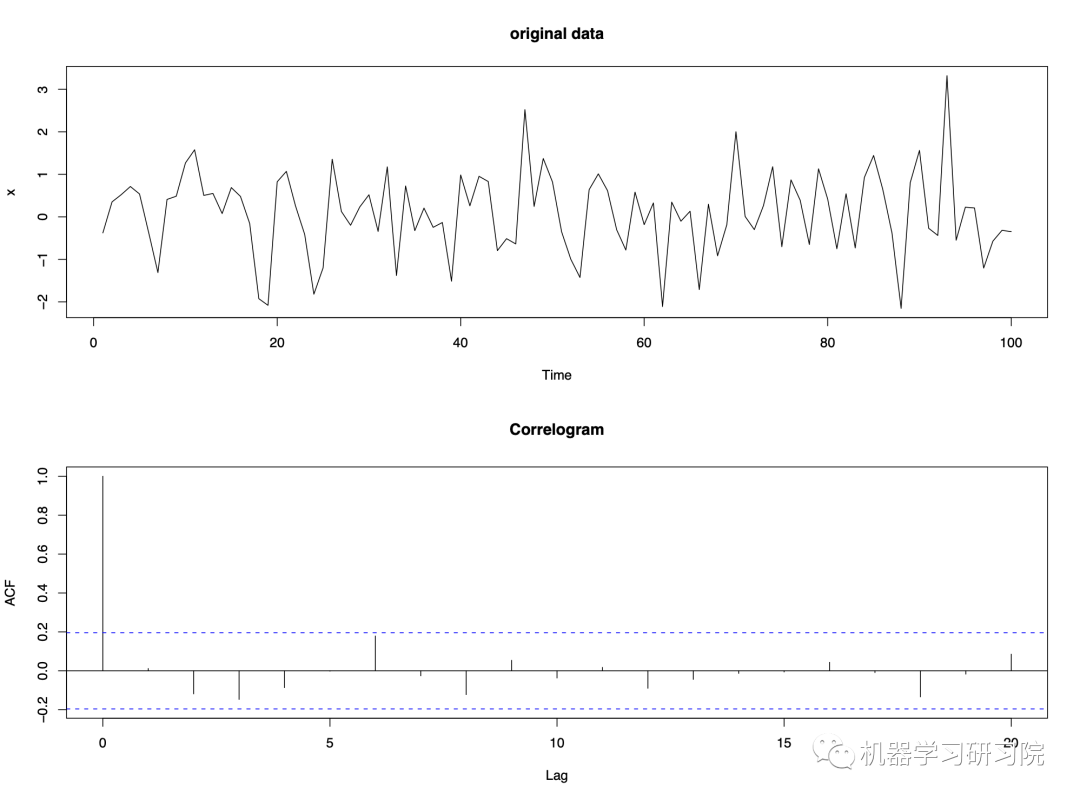
考虑由纯随机过程生成的时间序列，它没有趋势、季节性或短期相关性。原始数据和自相关图如下所示：

当时，，因为它是序列与其自身的相关性，通常忽略该值。
对于没有相关性的纯随机序列，通常在滞后 0 处等于 1，但在其他滞后处没有明显的相关性证据。

Example - short-term correlation

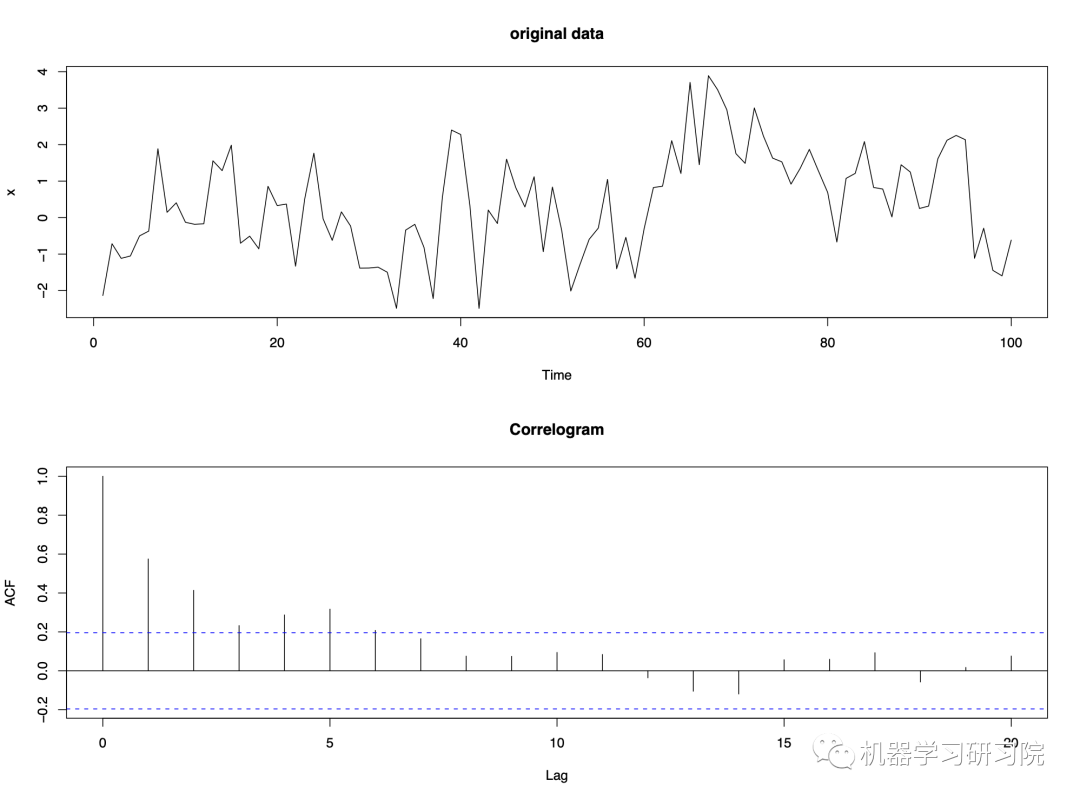
没有趋势或季节性但具有短期相关性的时间序列数据如下图所示，并且在前几个滞后时具有显着正的自相关，随后在较大滞后时值接近零。

Example - alternating data

没有趋势或季节性但在大值和小值之间交替的时间序列数据显示下图中，并且在奇数滞后时具有负自相关，在偶数滞后时具有正自相关。随着滞后的增加，自相关越来越接近于零。

Example - data with a trend

具有趋势的时间序列数据如下图所示，并且在滞后偏大时仍然具有正自相关。如果趋势随时间下降，则会观察到相同的相关图。

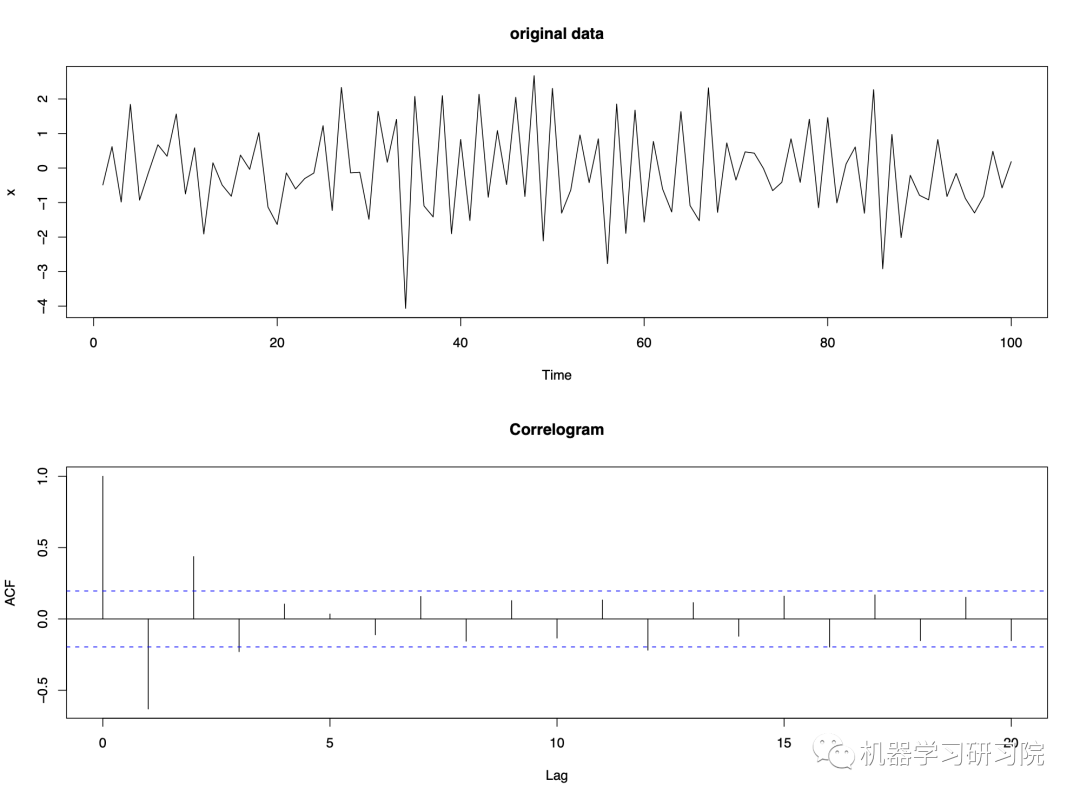
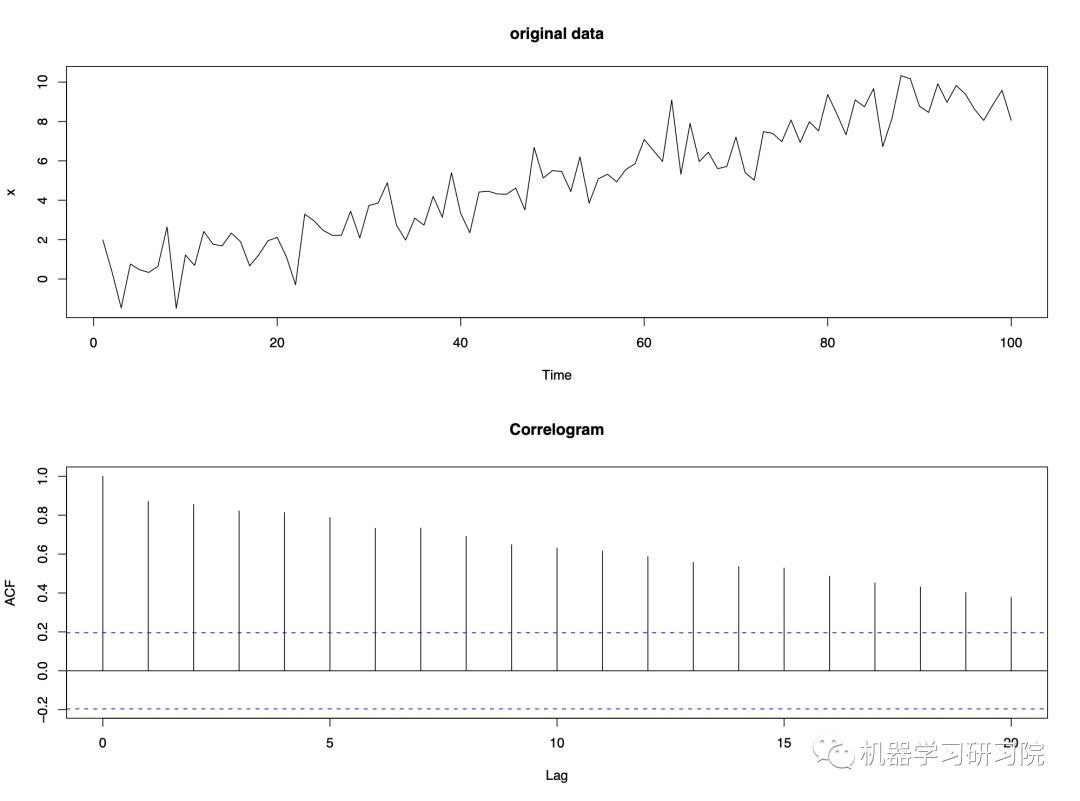
Example - data with a seasonal effect

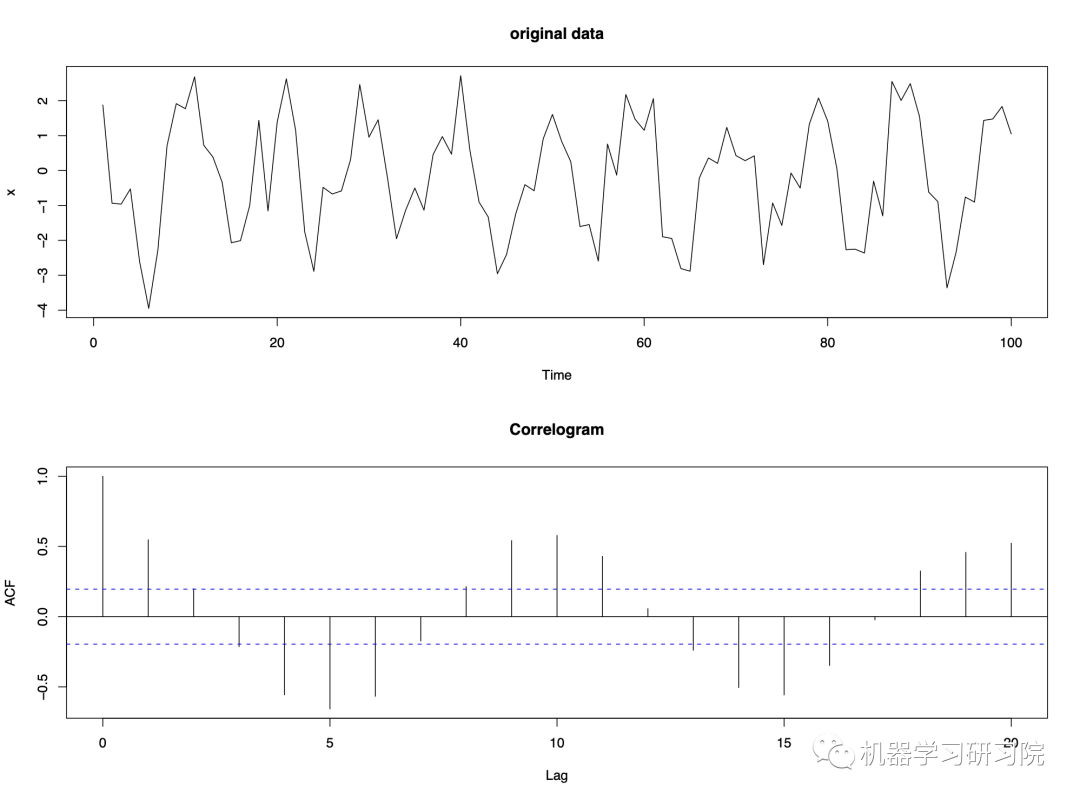
具有季节性影响的时间序列数据如下图所示，并且在相关图中具有规则的季节性模式。

Example - data with a trend and a seasonal effect

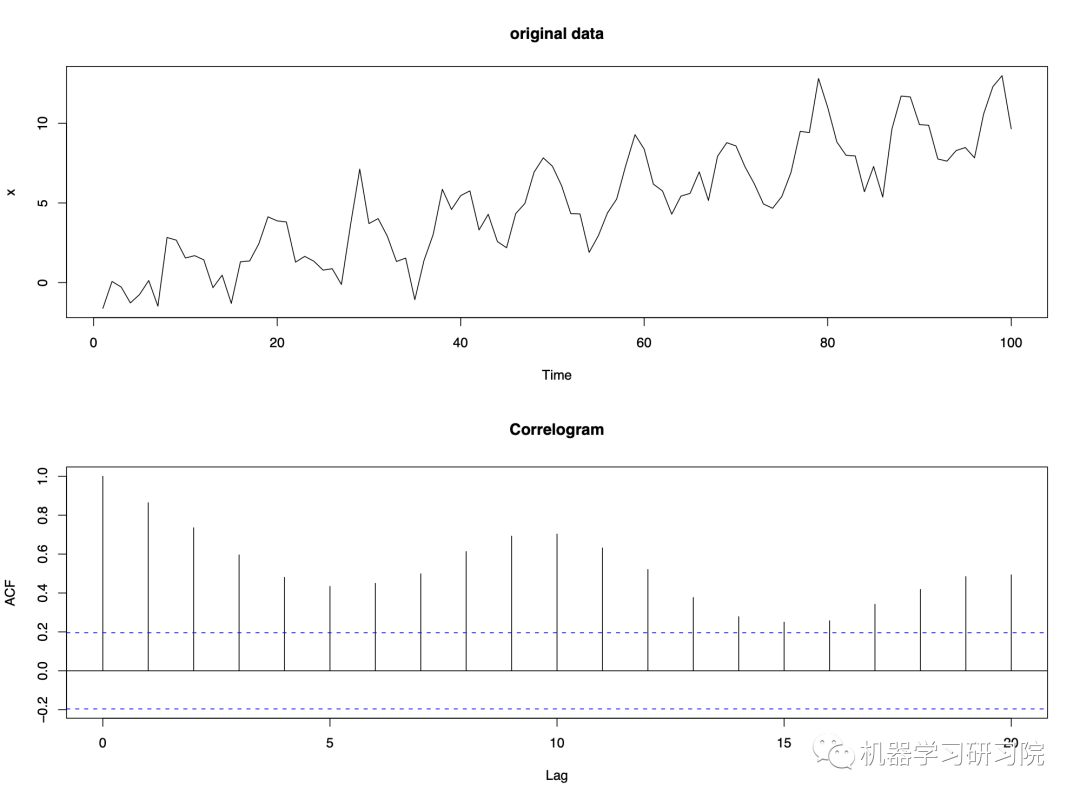
具有趋势和季节性影响的时间序列数据显示在下图中，并且在相关图中具有规则的季节性模式，由于趋势的存在，相关图通常具有正值。

平稳性分析

严格平稳
strictly stationary or strongly stationary

严格平稳是一种非常苛刻的条件，给定时序过程，对于所有的以及值，如果联合分布与相同，则该序列是严格平稳的。换句话说，换句话说，将序列的时间原点移动对其联合分布没有影响。

当，严格平稳意味着对于所有的，都有。这也说明时间序列的均值和方差为常数，即

和 , 当，严格平稳意味着对于所有的，都有

联合分布只取决于滞后

这反过来意味着理论协方差和相关函数只取决于滞后而不是原始位置。

严格平稳是非常严格的，而真实过程很少符合。一般只有纯粹的随机过程严格平稳，因此使用的更多的是弱平稳。

弱平稳

weakly stationary

给定时序过程，如果该时间序列过程是弱平稳的的，那么它需要满足以下条件：

均值是常数和有限的，即
方差是常数和有限的，即
自协方差和自相关函数仅取决于滞后，即以及

严格平稳性和弱平稳性之间的区别在于，后者仅假设前两个矩（均值和方差）随时间是恒定的，而前者假设较高的矩也是恒定的。

Example

定义一个随机游走过程，，且

其中是均为为 0 且方差为的随机过程。那么是非平稳的。因为

这说明方差是随时间变化的。

作者：daydaymoyu
来源：https://zhuanlan.zhihu.com/p/424609116
参考：https://bookdown.org/gary_a_napier/time_series_lecture_notes/ChapterOne.html#time-series-modelling