画一个带统计检验的PCoA分析结果
前情回顾
PERMANOVA原理解释:这个统计检验可用于判断PCA/PCoA等的分群效果是否显著!
经过前面的铺垫,下面来实战一下,理论应用于实际看看会出现什么问题?
PERMANOVA 实战 (一)
采用vegan包自带的一套数据(也解释了如何自己准备数据)看下PERMANOVA的具体代码和应用。
dune数据集描述
dune是一套包含了20个样品和30个物种丰度数据的统计表。其格式是常见OTU表转置后的格式,每一行是一个样品,每一列是一个物种 (检测指标)。
library(vegan)
data(dune)
dim(dune)
## [1] 20 30
head(dune)
## Achimill Agrostol Airaprae Alopgeni Anthodor Bellpere Bromhord Chenalbu Cirsarve Comapalu Eleopalu Elymrepe Empenigr Hyporadi
## 1 1 0 0 0 0 0 0 0 0 0 0 4 0 0
## 2 3 0 0 2 0 3 4 0 0 0 0 4 0 0
## 3 0 4 0 7 0 2 0 0 0 0 0 4 0 0
## 4 0 8 0 2 0 2 3 0 2 0 0 4 0 0
## 5 2 0 0 0 4 2 2 0 0 0 0 4 0 0
## 6 2 0 0 0 3 0 0 0 0 0 0 0 0 0如果我们有一个OTU丰度表,怎么转成这个格式呢?
otu_table <- read.table("otutable_rare",sep="\t", row.names=1, header=T)
as.data.frame(t(otu_table))
## OTU1 OTU2 OTU3
## Samp1 2 12 22
## Samp2 13 13 10
## Samp3 14 8 14
## Samp4 15 10 11dune.env是元数据信息,包含数据的分子信息、生存环境信息等,记录了5个因素 (同时包含连续变量信息和分组变量信息):
A1: 土壤厚度信息 a numeric vector of thickness of soil A1 horizon.Moisture: 湿度等级信息,分4个等级,1 < 2 < 4 < 5.Management: 分组信息,不同的管理方式 a factor with levels: BF (Biological farming), HF (Hobby farming), NM (Nature Conservation Management), and SF (Standard Farming).Use: 一个分组信息 an ordered factor of land-use with levels: Hayfield < Haypastu < Pasture.Manure: 一个分组信息,0 < 1 < 2 < 3 < 4.
data("dune.env")
head(dune.env)
## A1 Moisture Management Use Manure
## 1 2.8 1 SF Haypastu 4
## 2 3.5 1 BF Haypastu 2
## 3 4.3 2 SF Haypastu 4
## 4 4.2 2 SF Haypastu 4
## 5 6.3 1 HF Hayfield 2
## 6 4.3 1 HF Haypastu 2
summary(dune.env)
## A1 Moisture Management Use Manure
## Min. : 2.800 1:7 BF:3 Hayfield:7 0:6
## 1st Qu.: 3.500 2:4 HF:5 Haypastu:8 1:3
## Median : 4.200 4:2 NM:6 Pasture :5 2:4
## Mean : 4.850 5:7 SF:6 3:4
## 3rd Qu.: 5.725 4:3
## Max. :11.500这个文件就是我们常用的metadata文件,组织格式也一致,每一行是一个样品,每一列对应样品的不同属性。
绘制一个PcOA的图看一下
# 计算加权bray-curtis距离
dune_dist <- vegdist(dune, method="bray", binary=F)
dune_pcoa <- cmdscale(dune_dist, k=3, eig=T)
dune_pcoa_points <- as.data.frame(dune_pcoa$points)
sum_eig <- sum(dune_pcoa$eig)
eig_percent <- round(dune_pcoa$eig/sum_eig*100,1)
colnames(dune_pcoa_points) <- paste0("PCoA", 1:3)
dune_pcoa_result <- cbind(dune_pcoa_points, dune.env)
head(dune_pcoa_result)
## PCoA1 PCoA2 PCoA3 A1 Moisture Management Use Manure
## 1 -0.35473182 -0.25667235 0.31129225 2.8 1 SF Haypastu 4
## 2 -0.29462318 -0.18609437 0.03355954 3.5 1 BF Haypastu 2
## 3 -0.07276681 -0.29087086 -0.01169171 4.3 2 SF Haypastu 4
## 4 -0.06925423 -0.26419764 -0.01634735 4.2 2 SF Haypastu 4
## 5 -0.30706200 0.03031589 -0.09124310 6.3 1 HF Hayfield 2
## 6 -0.25302974 0.09420852 0.02814297 4.3 1 HF Haypastu 2
library(ggplot2)
ggplot(dune_pcoa_result, aes(x=PCoA1, y=PCoA2, color=Management)) +
labs(x=paste("PCoA 1 (", eig_percent[1], "%)", sep=""),
y=paste("PCoA 2 (", eig_percent[2], "%)", sep="")) +
geom_point(size=4
) + stat_ellipse(level=0.6) +
theme_classic()
## Too few points to calculate an ellipse
## Warning: Removed 1 row(s) containing missing values (geom_path).
样品中重复太少了,做不出置信椭圆。换个方式,用ggalt包中的geom_encircle把样品包起来。
# install.packages("ggalt")
library(ggalt)
ggplot(dune_pcoa_result, aes(x=PCoA1, y=PCoA2, color=Management, group = Management)) +
labs(x=paste("PCoA 1 (", eig_percent[1], "%)", sep=""),
y=paste("PCoA 2 (", eig_percent[2], "%)", sep="")) +
geom_point(size=5) +
geom_encircle(aes(fill=Management), alpha = 0.1, show.legend = F) +
theme_classic() + coord_fixed(1)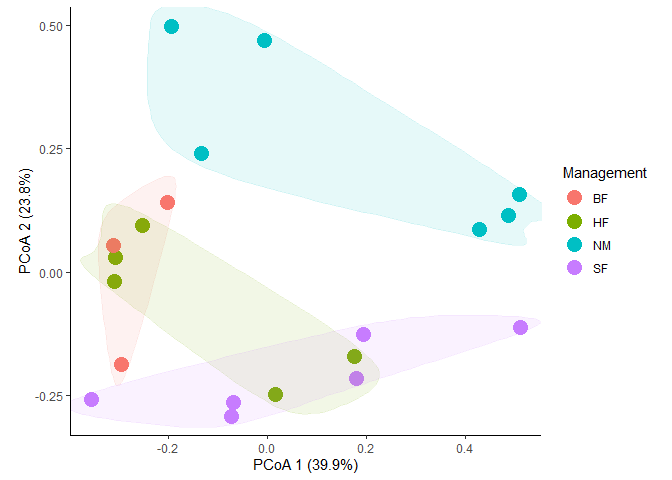
那么不同管理风格对物种组成是否有显著影响呢?
关注不同管理风格对物种组成是否有显著影响
假如关注的问题是:不同的管理风格对物种组成是否有显著影响?这就是一个典型的单因素非参多元方差分析。因素就是Management。
基于bray-curtis距离进行PERMANOVA分析,代码和结果如下:
dune是转置后的物种丰度表 (抽平或相对比例都行)Management是dune.env中的列名字,代表一列信息,可以是任意样品属性信息或分组信息permutations设置置换次数method指定距离计算方法R2值显示Management可以解释总体差异的34.2%,且P<0.05,表示不同的管理风格下的物种组成差异显著。当然还有
65.8%的差异是其它因素造成的。这通常是我们对
PcOA等降维图标记统计检验P值的常用方式。
注意:因为是随机置换,在未指定随机数种子时,每次执行的结果都会略有不同,但通常对结论没有影响。
# 基于bray-curtis距离进行计算
dune.div <- adonis2(dune ~ Management, data = dune.env, permutations = 999, method="bray")
dune.div
## Permutation test for adonis under reduced model
## Terms added sequentially (first to last)
## Permutation: free
## Number of permutations: 999
##
## adonis2(formula = dune ~ Management, data = dune.env, permutations = 999, method = "bray")
## Df SumOfSqs R2 F Pr(>F)
## Management 3 1.4686 0.34161 2.7672 0.004 **
## Residual 16 2.8304 0.65839
## Total 19 4.2990 1.00000
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1注意:因为是随机置换,在未指定随机数种子时,每次执行的结果都会略有不同,但通常对结论没有影响。也可以如下设置随机数种子,则结果稳定。
# 基于bray-curtis距离进行计算
set.seed(1)
dune.div <- adonis2(dune ~ Management, data = dune.env, permutations = 999, method="bray")
dune.div
## Permutation test for adonis under reduced model
## Terms added sequentially (first to last)
## Permutation: free
## Number of permutations: 999
##
## adonis2(formula = dune ~ Management, data = dune.env, permutations = 999, method = "bray")
## Df SumOfSqs R2 F Pr(>F)
## Management 3 1.4686 0.34161 2.7672 0.002 **
## Residual 16 2.8304 0.65839
## Total 19 4.2990 1.00000
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1把统计检验结果加到PcOA的图上。
dune_adonis <- paste0("adonis R2: ",round(dune.div$R2,2), "; P-value: ", dune.div$`Pr(>F)`)
# install.packages("ggalt")
library(ggalt)
ggplot(dune_pcoa_result, aes(x=PCoA1, y=PCoA2, color=Management, group = Management)) +
labs(x=paste("PCoA 1 (", eig_percent[1], "%)", sep=""),
y=paste("PCoA 2 (", eig_percent[2], "%)", sep=""),
title=dune_adonis) +
geom_point(size=5) +
geom_encircle(aes(fill=Management), alpha = 0.1, show.legend = F) +
theme_classic() + coord_fixed(1)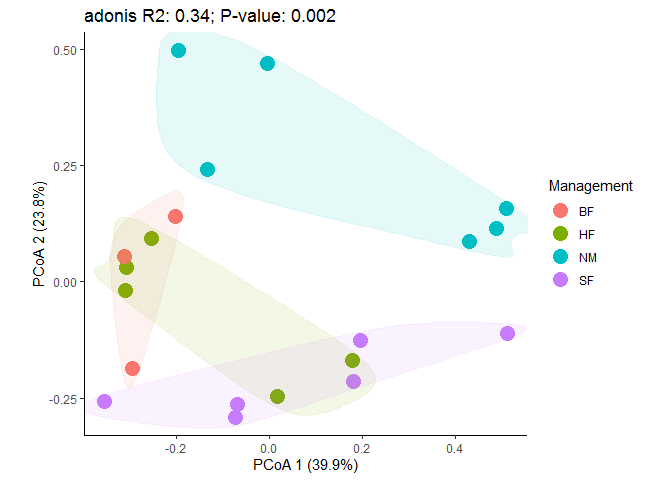
整体有差异了,后面就看看具体那两组之间有差异,哪两组之间无差异~~~
往期精品(点击图片直达文字对应教程)
后台回复“生信宝典福利第一波”或点击阅读原文获取教程合集