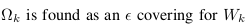【图神经网络】GCN-1（谱图卷积）-轻识

一、Address

Spectral Networks and Deep Locally Connected Networks on Graphs

地址：https://arxiv.org/pdf/1312.6203.pdf

作者提出了两种结构，一种是基于时域的层次聚类，并使用它们定义“局部”连接和池化

另一种是谱结构，利用了卷积在傅里叶域中的性质，通过找到相应的“傅里叶”基，可以将卷积扩展到一般的图。

作者通过实验证明，对于低维图，我们可以学习到独立于输入大小的卷积层参数，从而得到有效的深层结构。

局部性

加权图G=（Ω，W），其中Ω是大小为m的离散集，W是m×m对称非负矩阵。

利用图的权重定义局部性：例如，在W上定义邻域的一种简单方法是设置一个阈值δ>0，然后取邻域

深度局部连接网络

k代表第k个卷积层，表示第k层的输入节点数目，为第k层的聚类类数

代表第k-1层的滤波器数目以及第k层中每个节点的特征维数。代表输入数据，的shape为（）。表示第k层第j个滤波器的第i个值，h为激活函数，L为pooling操作

对于当前节点，按照如下方法取邻居：

这里体现了局部性（只取每个节点前k个邻居）（supp是支撑集，如果x和y节点不是邻域关系，的值为0）

连接体现在层与层之间的神经元数目是通过聚类得到的，上一层的聚类对应为下一层的神经元

第k层需要学习的参数个数为：

为 average support of the neighborhoods

F为权重的对角矩阵，V是拉普拉斯矩阵的特征向量矩阵，h为激活函数。是第K层上所有节点的第i个特征拼接形成的向量,是滤波器。

推导过程

离散卷积：

离散傅里叶变换：

离散傅里叶逆变换：

step 1

(上述推导来源于知乎回答：https://www.zhihu.com/question/47883434/answer/286401230)

(此处符号略不同，简单对比一下就可以理解了)

最后可得结论：f和g的卷积（时域）等于 f和g的频域乘积

step 2

根据亥姆霍兹方程有

其中是拉普拉斯算子

根据拉普拉斯的谱分解可得为拉普拉斯矩阵的特征值

代表时域信号,代表频域信号，有：

step 3

将step 2代入卷积公式：

令

得

FCN为全连接层（with N outputs），LRF为局部连接， MP 为max-pooling layer， SP为spectral层