「@Author：Runsen」

排序可能是所有的算法中最最基础和最最常用的了。排序是一个非常经典的问题，它以一定的顺序对一个数组（或一个列表）中的项进行重新排序。

排序算法有很多种，每个都有其自身的优点和局限性。

今天我们来学习最最简单的冒泡排序算法。

冒泡排序

要学习冒泡排序必须知道它的原理：

所谓冒泡，就是将元素两两之间进行比较，谁大就往后移动，直到将最大的元素排到最后面，接着再循环一趟，从头开始进行两两比较，而上一趟已经排好的那个元素就不用进行比较了。

下面，我们就进入代码环节。

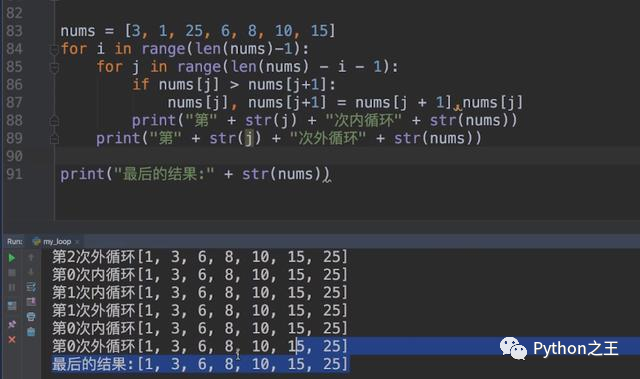
Python实现冒泡排序 现在，我给你一个nums = [3,1,25,6,8,10,15]，要求你用Python将nums实现冒泡排序。

看上去很难入手，其实很简单，我先给出代码

nums = [3,1,25,6,8,10,15]
for i in range(len(nums)-1):
    for j in range(len(nums) - i -1):
        if nums[j] > nums[j+1]:
            nums[j],nums[j+1] =  nums[j+1],nums[j]
        print("第"+str(j)+"次内循环"+str(nums))
    print("第"+str(i)+"次外循环"+str(nums))
print("最后的结果"+str(nums))

我们先遍历nums，这不就是我们的range(len(nums)-1)，至于为什么是range(len(nums)-1)，其实就是我们的下标从0开始的，len(nums)返回是7，range是左开右闭，但是冒泡排序，我们只需要取到nums[5] = 10 就足够了，所以这里range(len(nums)-1)，取到[3,1,25,6,8,10]。

然后，我们在遍历之后的nums，比如i = 0，我们将j取值范围到len(nums) - i -1，用nums[j] > nums[j+1]判断两两的大小, 每次内循环将最大的移到最右边。

每一次内循环的目的就是将当中最大的移到最右边，而每一次外循环的目的就是当最大的移到最右边后，缩小范围，再寻找最大的数，再把它移到最右边。

我们执行上面的代码的结果如下：

第0次内循环[1, 3, 25, 6, 8, 10, 15]
第1次内循环[1, 3, 25, 6, 8, 10, 15]
第2次内循环[1, 3, 6, 25, 8, 10, 15]
第3次内循环[1, 3, 6, 8, 25, 10, 15]
第4次内循环[1, 3, 6, 8, 10, 25, 15]
第5次内循环[1, 3, 6, 8, 10, 15, 25]
第0次外循环[1, 3, 6, 8, 10, 15, 25]
第0次内循环[1, 3, 6, 8, 10, 15, 25]
第1次内循环[1, 3, 6, 8, 10, 15, 25]
第2次内循环[1, 3, 6, 8, 10, 15, 25]
第3次内循环[1, 3, 6, 8, 10, 15, 25]
第4次内循环[1, 3, 6, 8, 10, 15, 25]
第1次外循环[1, 3, 6, 8, 10, 15, 25]
第0次内循环[1, 3, 6, 8, 10, 15, 25]
第1次内循环[1, 3, 6, 8, 10, 15, 25]
第2次内循环[1, 3, 6, 8, 10, 15, 25]
第3次内循环[1, 3, 6, 8, 10, 15, 25]
第2次外循环[1, 3, 6, 8, 10, 15, 25]
第0次内循环[1, 3, 6, 8, 10, 15, 25]
第1次内循环[1, 3, 6, 8, 10, 15, 25]
第2次内循环[1, 3, 6, 8, 10, 15, 25]
第3次外循环[1, 3, 6, 8, 10, 15, 25]
第0次内循环[1, 3, 6, 8, 10, 15, 25]
第1次内循环[1, 3, 6, 8, 10, 15, 25]
第4次外循环[1, 3, 6, 8, 10, 15, 25]
第0次内循环[1, 3, 6, 8, 10, 15, 25]
第5次外循环[1, 3, 6, 8, 10, 15, 25]
最后的结果[1, 3, 6, 8, 10, 15, 25]

我们可以看到，第0次外循环，已经将25放在了最右边，第1次外循环确定把15放到最右边，这样从右往左，从大到小，这就是完整的冒泡排序。

冒泡排序的时间复杂度是：假设被排序的数列中有N个数。遍历一趟的时间复杂度是，需要遍历多少次呢？N-1次！因此，冒泡排序的时间复杂度。

冒泡排序是稳定的算法：它满足稳定算法的定义；所谓算法稳定性指的是对于一个数列中的两个相等的数a[i]=a[j]，在排序前,a[i]在a[j]前面，经过排序后a[i]仍然在a[j]前，那么这个排序算法是稳定的。

下面是Java冒泡排序代码。

public class Sort {
  public static void sort() {
    Scanner input = new Scanner(System.in);
    int sort[] = new int[10];
    int temp;
    System.out.println("请输入10个排序的数据：");
    for (int i = 0; i < sort.length; i++) {
      sort[i] = input.nextInt();
    }
    for (int i = 0; i < sort.length - 1; i++) {
      for (int j = 0; j < sort.length - i - 1; j++)       {
        if (sort[j] < sort[j + 1]) {
          temp = sort[j];
          sort[j] = sort[j + 1];
          sort[j + 1] = temp;
        }
      }
    }
    System.out.println("排列后的顺序为：");
    for(int i=0;i      System.out.print(sort[i]+"   ");
    }
  }
  public static void main(String[] args) {
    sort();
  }
}

JavaScript冒泡排序代码。

function sort(arr) {
    for (var i = 0; i < arr.length - 1; i++) {  //外部for循环
        for (var j = 0; j < arr.length - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                var temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
    return arr;
}

//举例如下
var arr = sort([1, 7, 4, 97, 23, 45]);
console.log(arr);

❝

本文已收录 GitHub，传送门~^[1] ，里面更有大厂面试完整考点，欢迎 Star。

❞

Reference