深度学习必须掌握的 13 种概率分布

转自 | 深度学习前沿

作为机器学习从业者，你需要知道概率分布相关的知识。这里有一份最常见的基本概率分布教程，大多数和使用 python 库进行深度学习有关。

一 概率分布概述

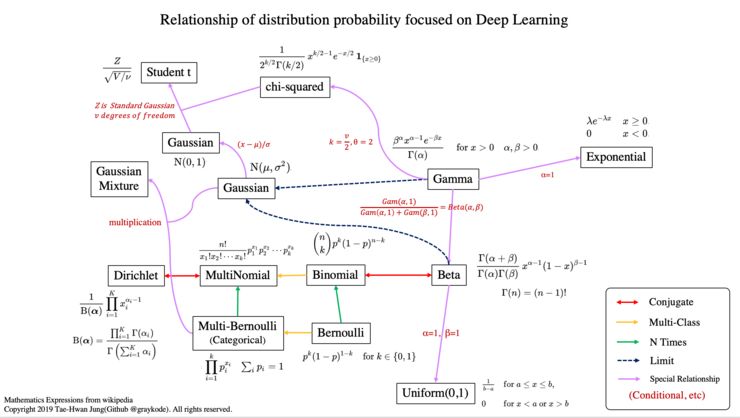
• 共轭意味着它有共轭分布的关系。
  

在贝叶斯概率论中，如果后验分布 p（θx）与先验概率分布 p（θ）在同一概率分布族中，则先验和后验称为共轭分布，先验称为似然函数的共轭先验。共轭先验维基百科在这里（https://en.wikipedia.org/wiki/Conjugate_prior）。

• 多分类表示随机方差大于 2。
  

• n 次意味着我们也考虑了先验概率 p（x）。
  

• 为了进一步了解概率，我建议阅读 [pattern recognition and machine learning，Bishop 2006]。

二 分布概率与特征

1.均匀分布（连续）

代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/uniform.py

均匀分布在 [a，b] 上具有相同的概率值，是简单概率分布。

2.伯努利分布（离散）

代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/bernoulli.py

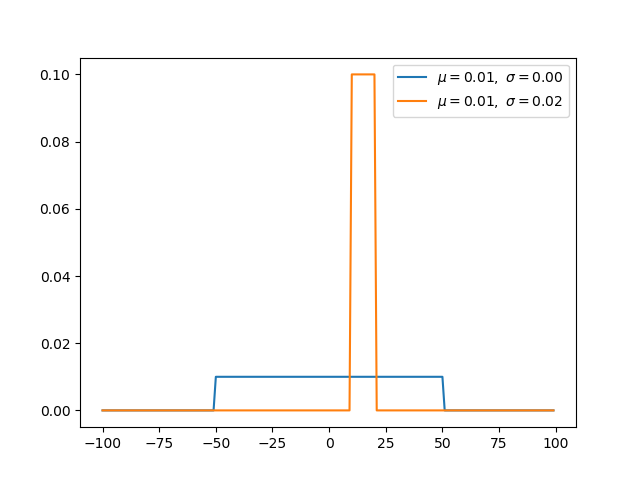
• 先验概率 p（x）不考虑伯努利分布。因此，如果我们对最大似然进行优化，那么我们很容易被过度拟合。
  

• 利用二元交叉熵对二项分类进行分类。它的形式与伯努利分布的负对数相同。

3.二项分布（离散）

代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/binomial.py 

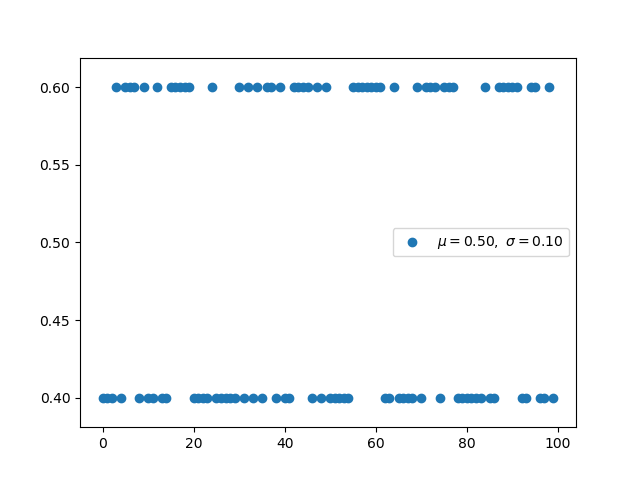
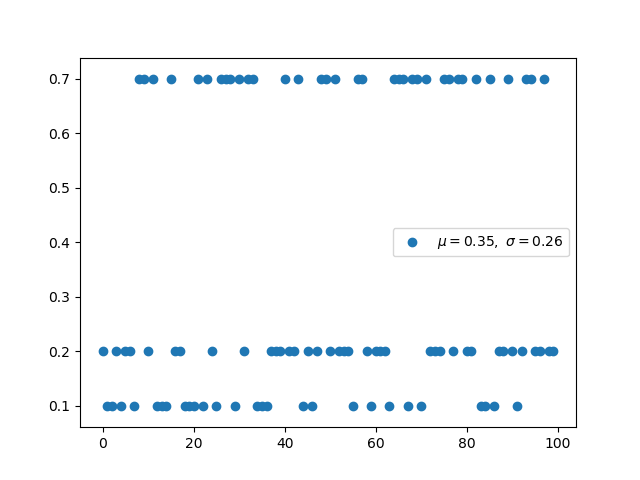
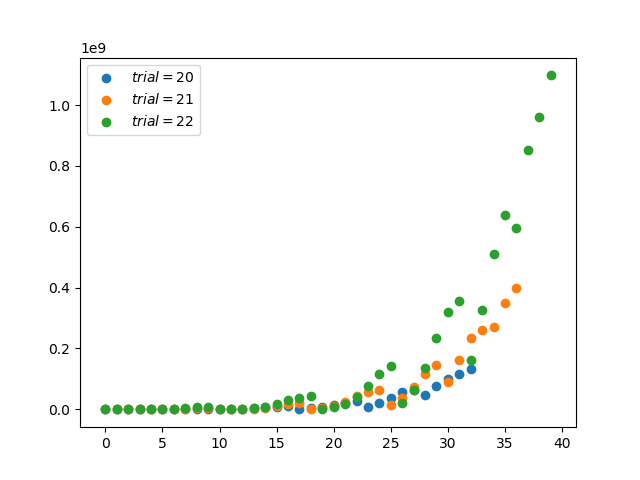
• 参数为 n 和 p 的二项分布是一系列 n 个独立实验中成功次数的离散概率分布。
  
• 二项式分布是指通过指定要提前挑选的数量而考虑先验概率的分布。

4.多伯努利分布，分类分布（离散）

代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/categorical.py

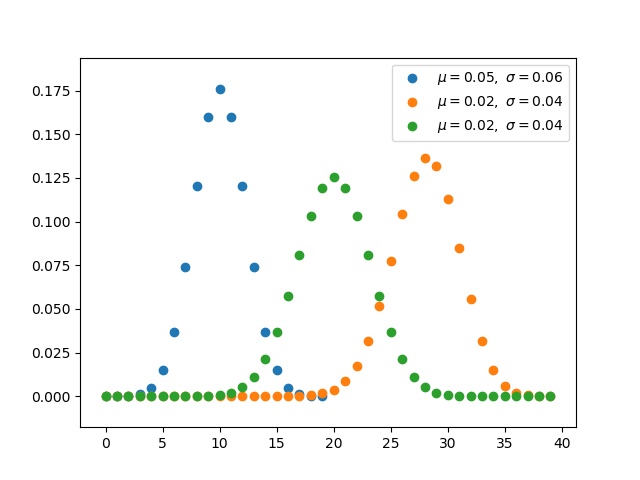
• 多伯努利称为分类分布。
  
• 交叉熵和采取负对数的多伯努利分布具有相同的形式。

5.多项式分布（离散）

代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/multinomial.py

多项式分布与分类分布的关系与伯努尔分布与二项分布的关系相同。

6.β分布（连续）

代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/beta.py

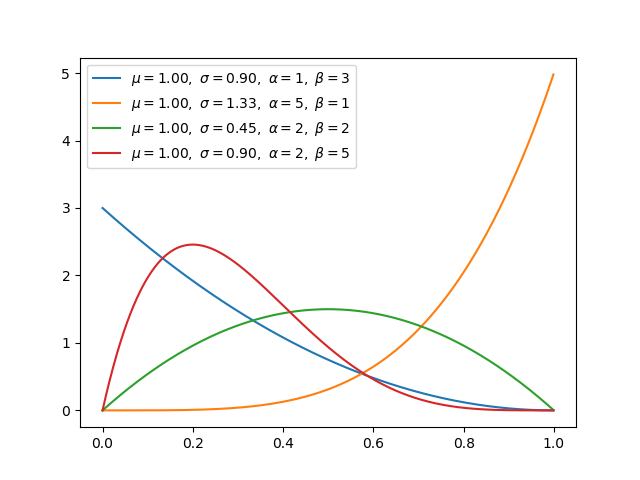
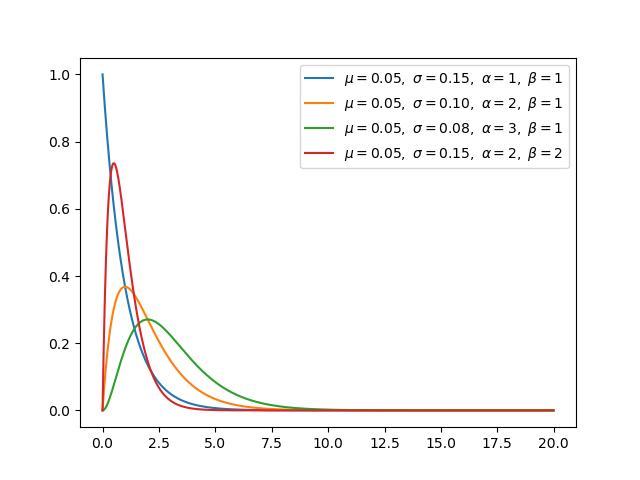
• β分布与二项分布和伯努利分布共轭。
  
• 利用共轭，利用已知的先验分布可以更容易地得到后验分布。
  
• 当β分布满足特殊情况（α=1，β=1）时，均匀分布是相同的。

7.Dirichlet 分布（连续）

代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/dirichlet.py 

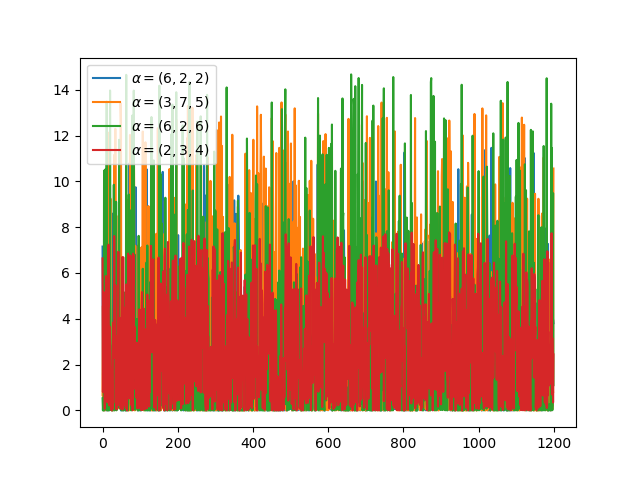
• dirichlet 分布与多项式分布是共轭的。
  
• 如果 k=2，则为β分布。

8.伽马分布（连续）

代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/gamma.py

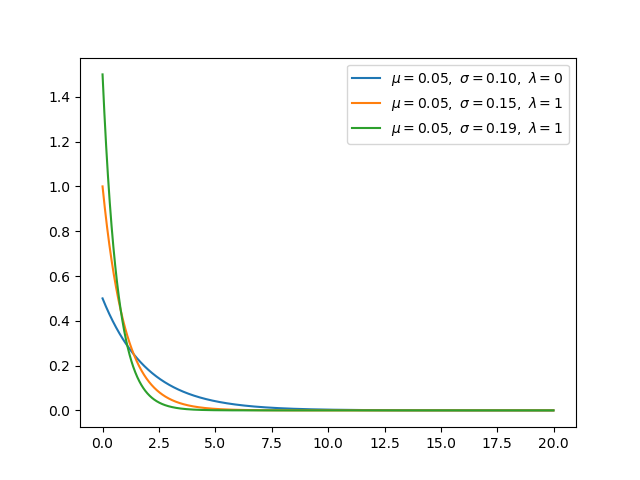
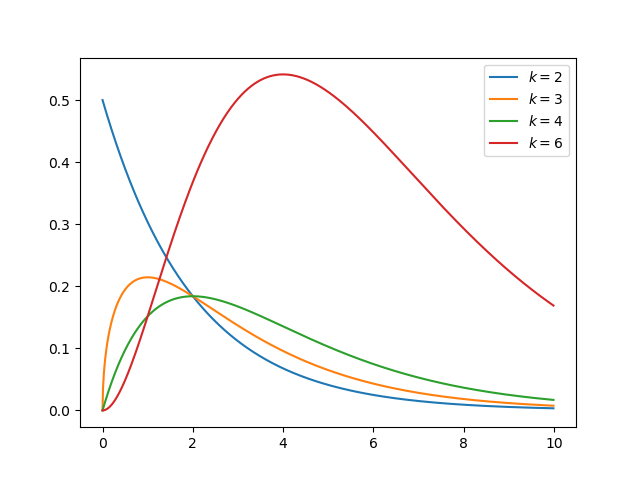
• 如果 gamma（a，1）/gamma（a，1）+gamma（b，1）与 beta（a，b）相同，则 gamma 分布为β分布。
  
• 指数分布和卡方分布是伽马分布的特例。

9.指数分布（连续）

代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/exponential.py

指数分布是 α 为 1 时 γ 分布的特例。

10.高斯分布（连续）

代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/gaussian.py

高斯分布是一种非常常见的连续概率分布。

11.正态分布（连续）

代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/normal.py

正态分布为标准高斯分布，平均值为 0，标准差为 1。

12.卡方分布（连续）

代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/chi-squared.py

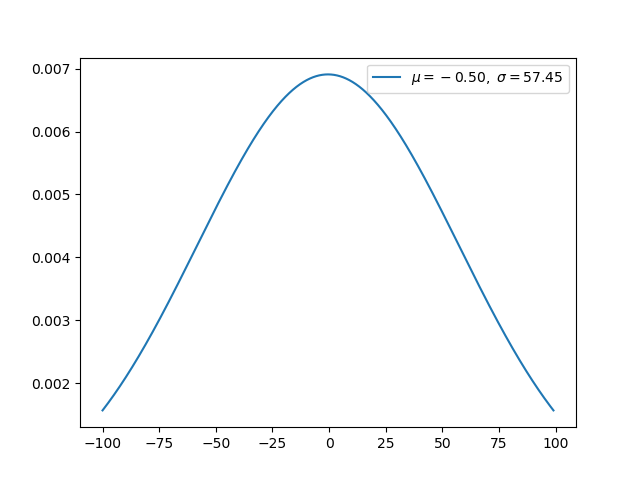
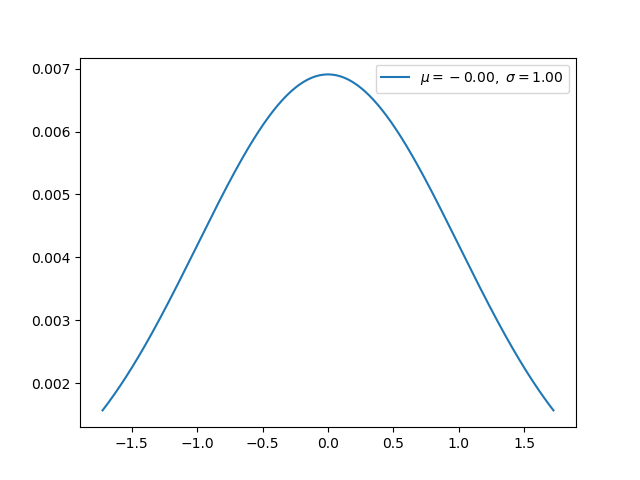
• k 自由度的卡方分布是 k 个独立标准正态随机变量的平方和的分布。
  

• 卡方分布是 β 分布的特例

13.t 分布（连续）

代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/student-t.py

t 分布是对称的钟形分布，与正态分布类似，但尾部较重，这意味着它更容易产生远低于平均值的值。

via：https://github.com/graykode/distribution-is-all-you-need