七十五、栈+双指针，头条当年接雨水问题

「@Author：Runsen」

❝

编程的本质来源于算法，而算法的本质来源于数学，编程只不过将数学题进行代码化。「---- Runsen」

❞

清晨的时候，熟睡中的我被咯吱咯吱作响的窗子吵醒，起身一看，窗外正是狂风大作，不一会儿便下起了爆雨，来也快，去也快，不一会儿天亮便放晴了，院子被雨水洗刷得很干净，猛的吸一口气，灌入的是满鼻的泥土芳香。

不知不觉我唱起了烟花易冷

雨纷纷，旧故里草木深。
我听闻，你始终一个人。

看着雨水，于是，我打开Leetcode，刷上了Leetcode  42  接雨水。

Leetcode 第42 题  接雨水

题目不说了，给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

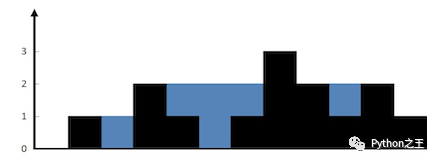
本题的关键点在于，具备什么条件的格子可以存水？

「(1) 空间未被柱子占据；(2) 左右两侧均有比当前位置高或者等于的柱子。」

其实就是寻找凹陷的地方。

知道这个就是好办了。看看我标题就知道了方法就是栈+双指针。此题不建议用dp，这种dp还是挺难想的。

常规做法

最朴素的想法是暴力法。针对每一个数组的值，遍历数组以获得当前位置对雨水的贡献量，这种方式的时间复杂度为，空间复杂度为。

就是找到最高的柱子，分成两份，寻找凹陷的地方，计算面积即可。

# @Author：Runsen
# @Date：2020/09/30

class Solution:
    def trap(self, height: List[int]) -> int:
      # 寻找最大的柱子
        maxindex = maxvalue = 0
        n = len(height)
        for i in range(n):
            if height[i] > maxvalue:
                maxvalue = height[i]
                maxindex = i
        # 左边找凹槽
        a = res = 0
        for i in range(maxindex):
            if a < height[i]:
                a = height[i]
                continue
            res = res + a - height[i]
        # 右边找凹槽
        b = 0 
        for i in range(n-1,maxindex,-1):
            if b < height[i]:
                b = height[i]
                continue
            res = res + b - height[i]
        return res

双指针

双指针的做法计算柱子不是一个一个的计算，而是按照一层一层的算。

我们可以通过左右指针的状态，遍历出来每个高度下的最大接水宽度。当左右指针指向的区域高度小于high时，左右指针都向中间移动，直到指针指向区域大于等于high的值。若不小于high，则指针不移动。

# @Author：Runsen
# @Date：2020/09/30

class Solution:
    def trap(self, height: List[int]) -> int:
        n = len(height)
        left, right = 0, n - 1
        result, high = 0, 1
        while (left <= right):
         # 这里需要注意left <= right，如果出现了一层只有一个的情况
            while (left <= right and height[left] < high):
                left += 1
            while (right >= left and height[right] < high):
                right -= 1
            high += 1
            result += right - left + 1
        return result - sum(height)

栈

产生凹陷的地方才能存储雨水，那么高度一定是先减后增，所以思路就是维护一个高度递减的栈。

步骤非常简单：① 设置一个高度递减的栈

② 找出先增后减的转折点的位置

③ 求出那部分凹陷的面积

④ 遍历，继续求出其他的面积

# @Author：Runsen
# @Date：2020/09/30

class Solution:
    def trap(self, height: List[int]) -> int:
        length=len(height)
        if length < 3:
            return 0
        res = 0
        # 设置一个高度递减的栈
        stack=[]
        for index in range(0, length):  # 遍历index
         # 当栈>0并且index位置的值>栈里最后的一个元素的值
            while len(stack)>0 and height[index] > height[stack[-1]]:   
             # 弹出栈中最后一个元素
                top=stack.pop()     
                if len(stack) == 0:
                    break
                # 计算凹陷的高度
                h = min(height[stack[-1]], height[index]) - height[top]  
                # 计算凹陷的宽度
                dist = index - stack[-1] - 1   
                # 求出存水的量
                res += (dist * h)       
            stack.append(index)
        return res

想不到的做法

正当我用上面三种完成了AC，看了下别人的做法，

想到了一种绝妙的方法，代码精简。如下图所示：

一次循环中，用左右两个指针，左指针记录左边遇到的最大值，右指针记录右边遇到的最大值， 每轮循环将两个最大值加起来，并且减去当前柱子的高度。

当循环结束时，可以发现，我们多加了一个大矩形的面积，所以最后返回的时候把这个矩形面积减掉就是我们要的结果。

class Solution:
    def trap(self, height: List[int]) -> int:
        lmax, rmax, res = 0, 0, 0
        for i in range(len(height)):
            lmax = max(lmax, height[i])
            rmax = max(rmax, height[-1-i])
            res += lmax + rmax - height[i]
        return res - lmax * len(height)

我把作者和链接写了上去

作者：821218213
链接：https://leetcode-cn.com/problems/trapping-rain-water/solution/42py3liang-chong-fang-fa-yi-ji-xiang-xi-si-lu-by-8/

看到这样的做法，发现自己就是一条菜。今天的算法到了这里差不多了。

❝

本文已收录 GitHub，传送门~^[1] ，里面更有大厂面试完整考点，欢迎 Star。

❞

Reference