【LM】线性代数的几何理解
以前读初高中的时候懒到不行,数理化公式从来不背,还好手速够快,每到考试就现场推导,久了也就记住了。到了大学背了许多公式,却没理解其中本质,反而捏在手里使不出来。
去年在做人体模型渲染,其中有三维坐标点的旋转平移。弱智的我还在把各维度坐标代入变换公式,再组合成新坐标。
然后看了眼文档..
好家伙,矩阵这玩意儿怕是啥也想不起来了。索性重新回来复习一下线性代数,顺便做个学习笔记。
之前看了刘剑平老师的《线性代数及其应用》,翻开后密密麻麻的代数式和文字直接劝退我了。这次参考3Blue1Brown的《线性代数本质》,以几何的角度来理解线性代数。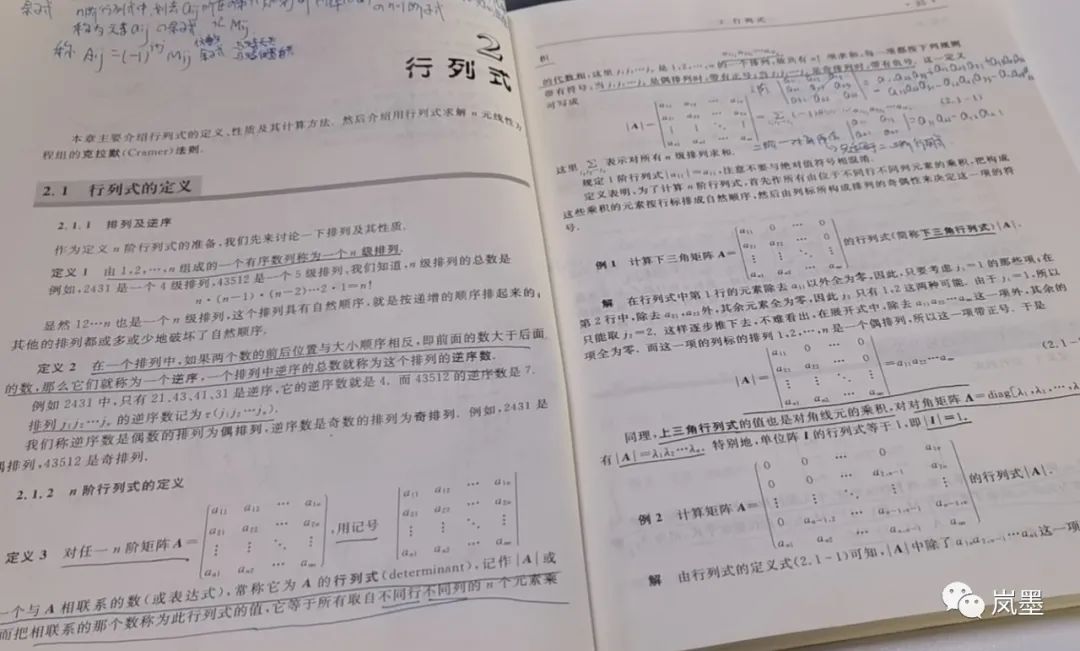
线性组合:所有向量都可以看成是由一组基底向量缩放再相加而成。空间:即两个向量所有线性组合形成的区域。例如两个线性无关的向量可以形成平面,三个线性无关的向量可以组成空间。
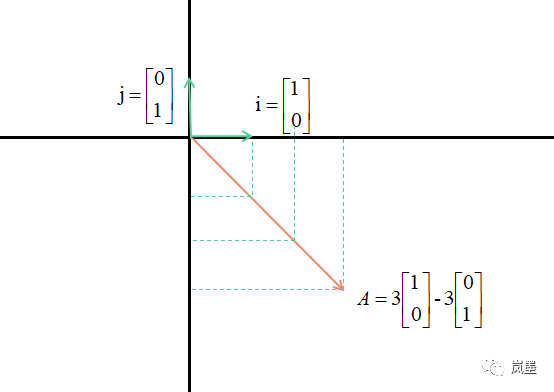
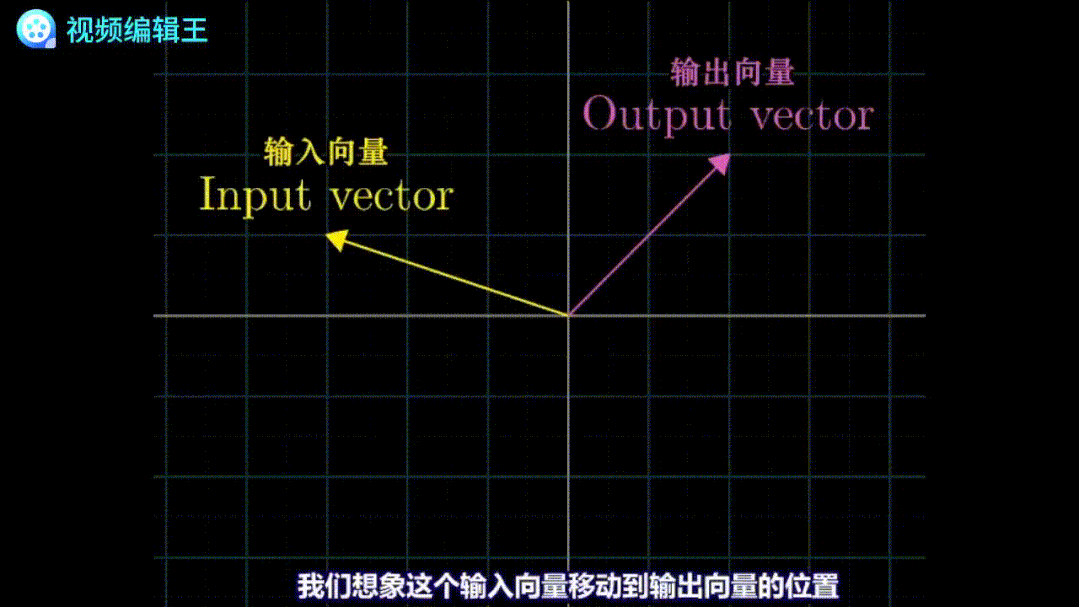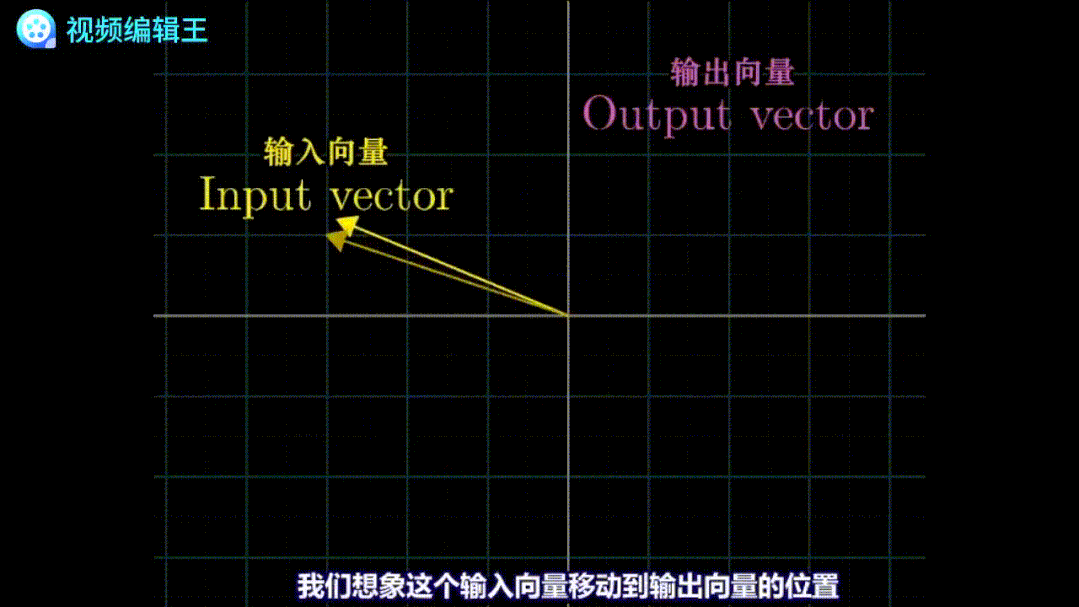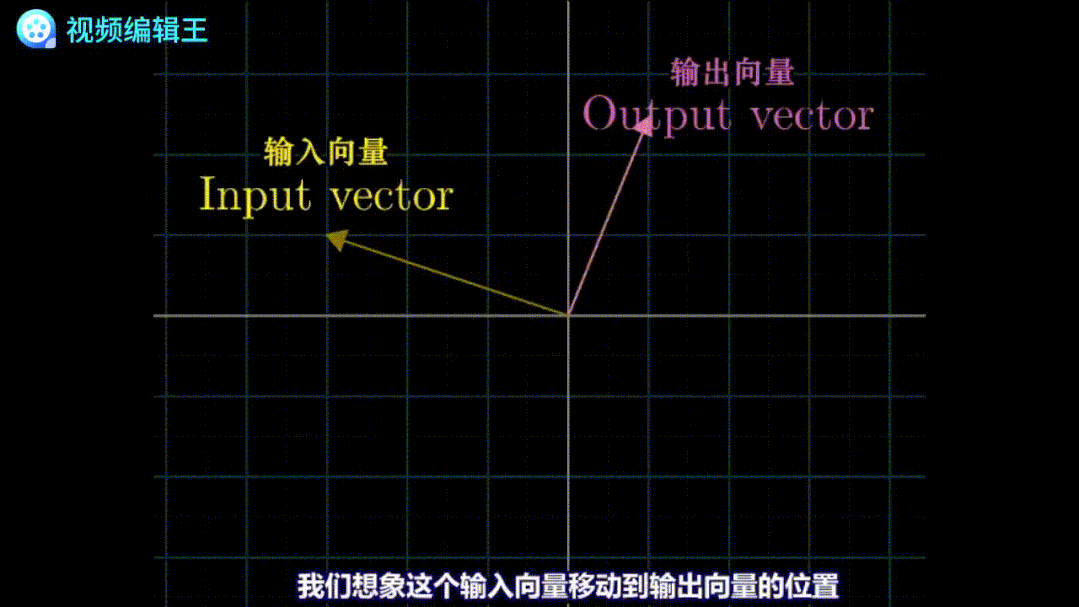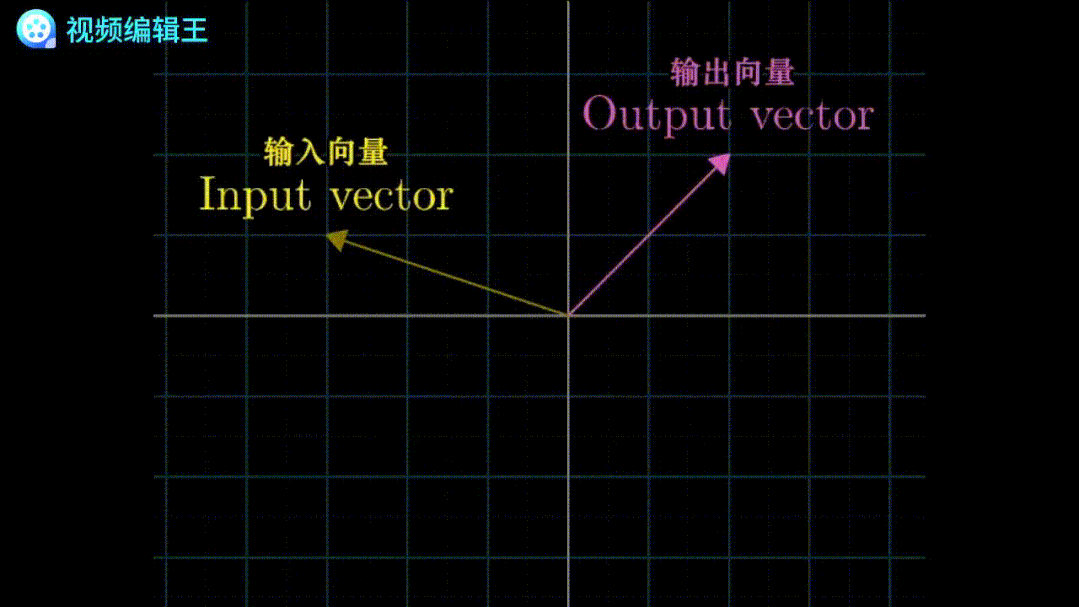
线性变换线性变换可以类比函数的定义:输入一个向量,经过某种变换,输出另一个向量。线性变换可以看作是关于向量的函数,也可以看作是一种可视化函数。
将一个线性变换,运用到整个维度中,即可以看成是把整个空间变换。
例如一个二维线性变换,可以把一个平面进行伸缩或剪切。
线性变换和非线性变换的几何区别在于:线性变换必须保持原点不动,且直线变换后依旧是直线。

线性变换的好处在于,变换前后的某个向量A,可以用相同的式子表示为基底向量的组合。
在二维平面中,只需要追踪两个基底[1, 0]和[0, 1]变换后的位置,就可以推断出任意向量经过变换后的位置。举个例子,假如二维平面内的两个基底[1, 0]和[0, 1],变换后成了[1, -2]和[3, 0],那任意一个向量[x,y],经过变换后都可以表示为:
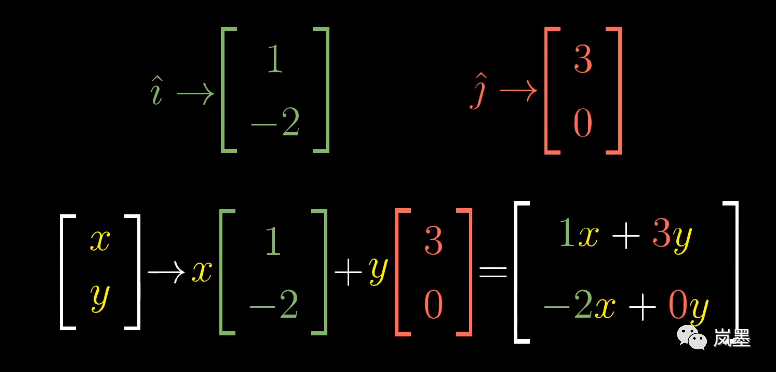
也就是说,一个二维线性变换,可以简单的用四个数字表示,即变换后的基底向量[1, -2]和[3, 0]。

矩阵:用来描述线性变换的信息。描述一个二维线性变换需要用到两个基底向量。把这两个向量写到一起,它就变成了一个2x2的矩阵。
例如下面这个矩阵,向我们描述了一个线性变换的信息:基底[1, 0]变换到了[a, c],基底[0, 1]变换到了[b, d]。
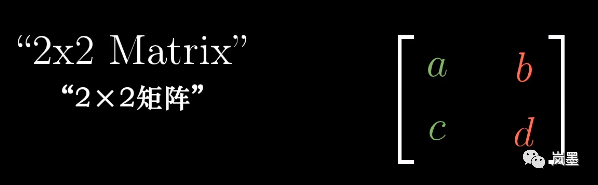
旋转:绕着原点旋转空间的一种变换。例如矩阵
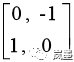 代表基底[1,0]和[0,1]各自旋转90°。
代表基底[1,0]和[0,1]各自旋转90°。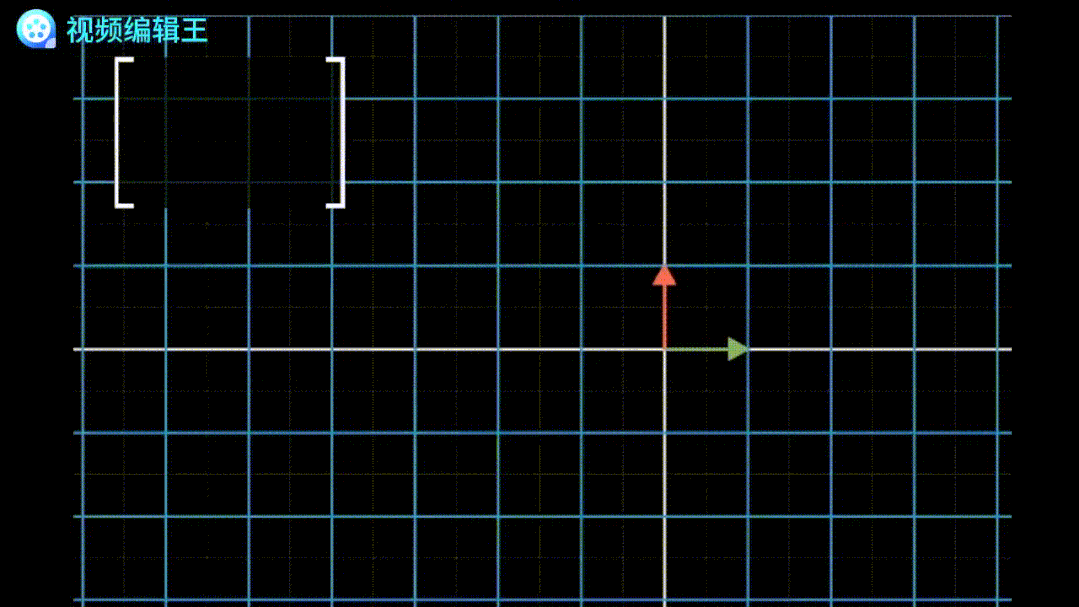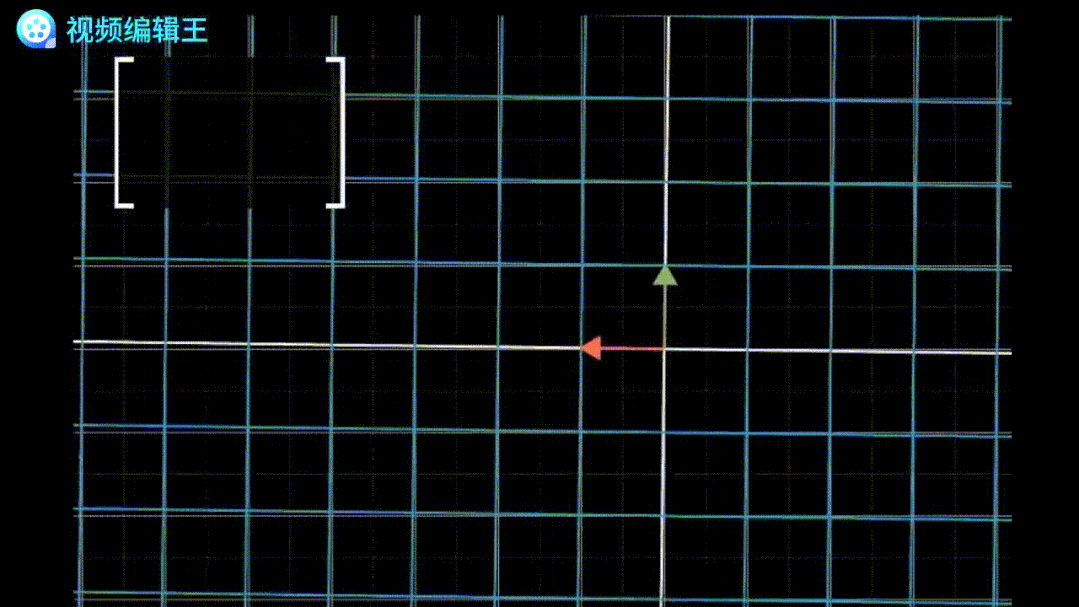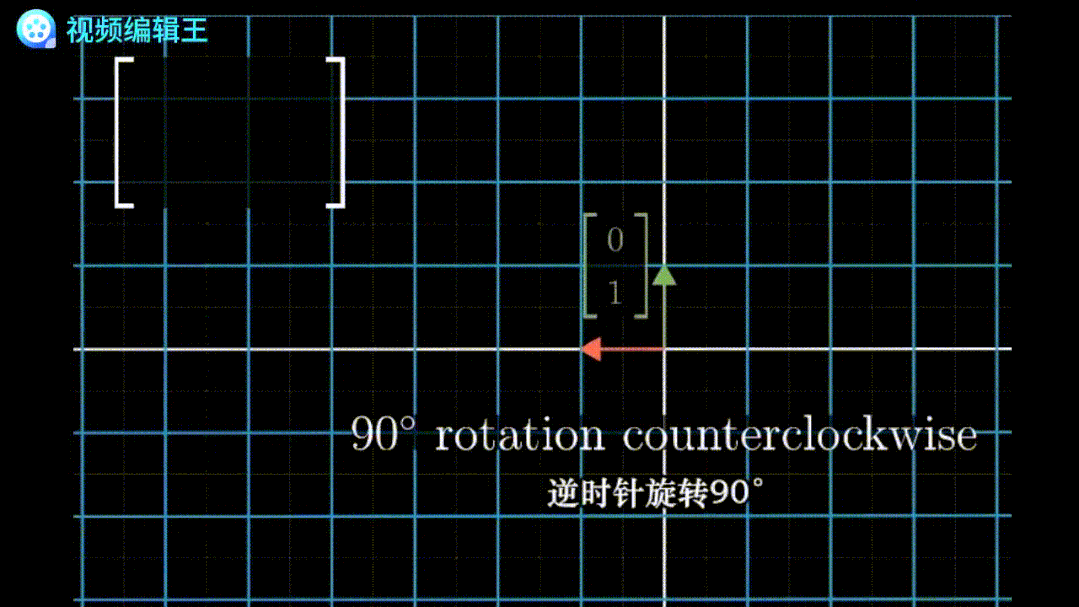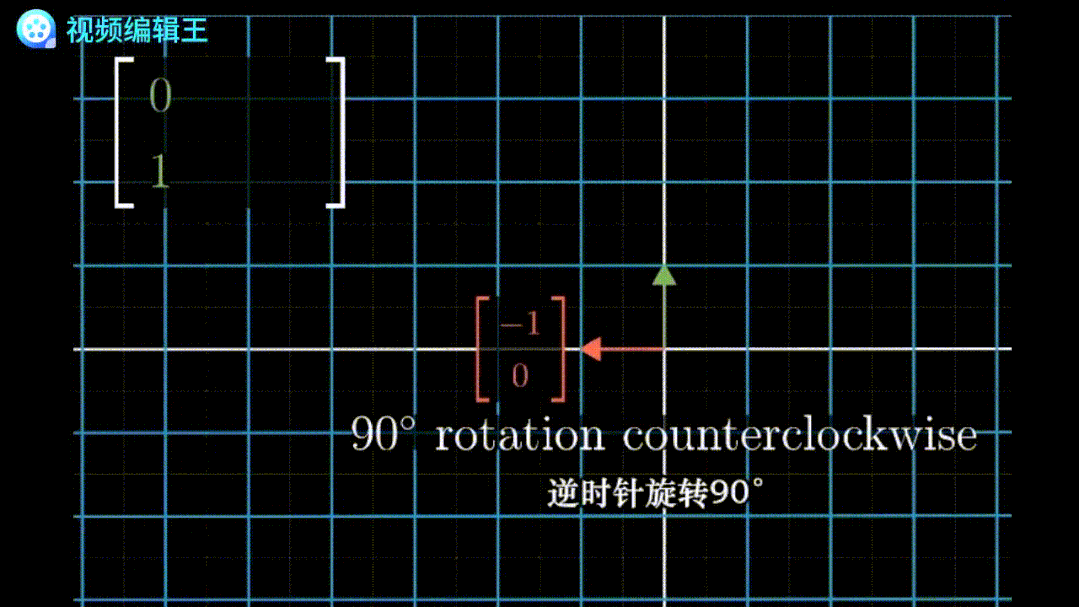 剪切:保持一个基底不变,移动另一个基底。例如矩阵
剪切:保持一个基底不变,移动另一个基底。例如矩阵 表示基底[0,1]平移到了[1,1]的位置,从而将整个平面扭曲。
表示基底[0,1]平移到了[1,1]的位置,从而将整个平面扭曲。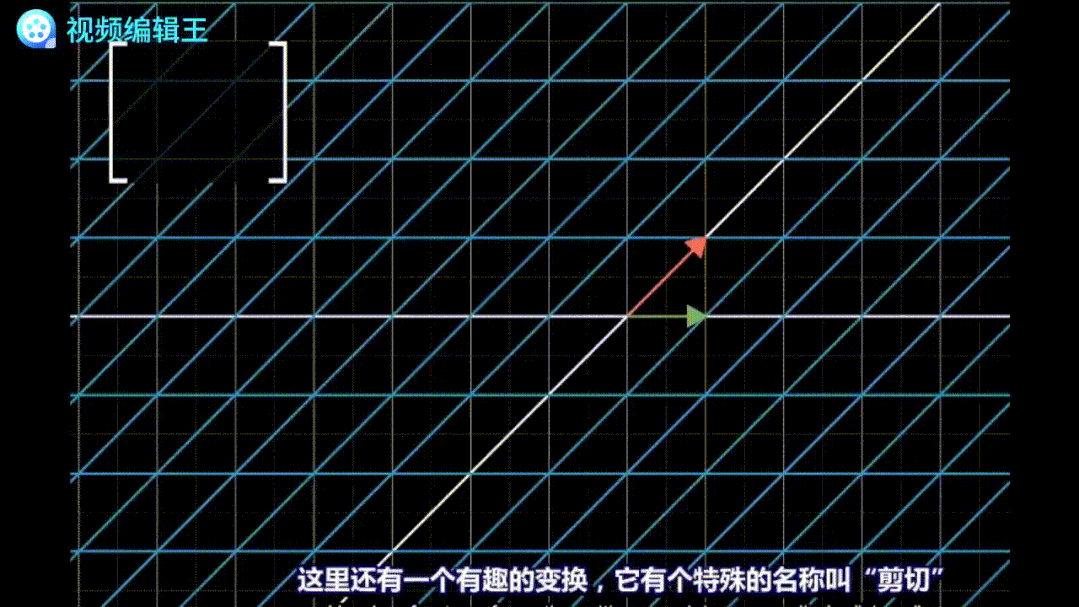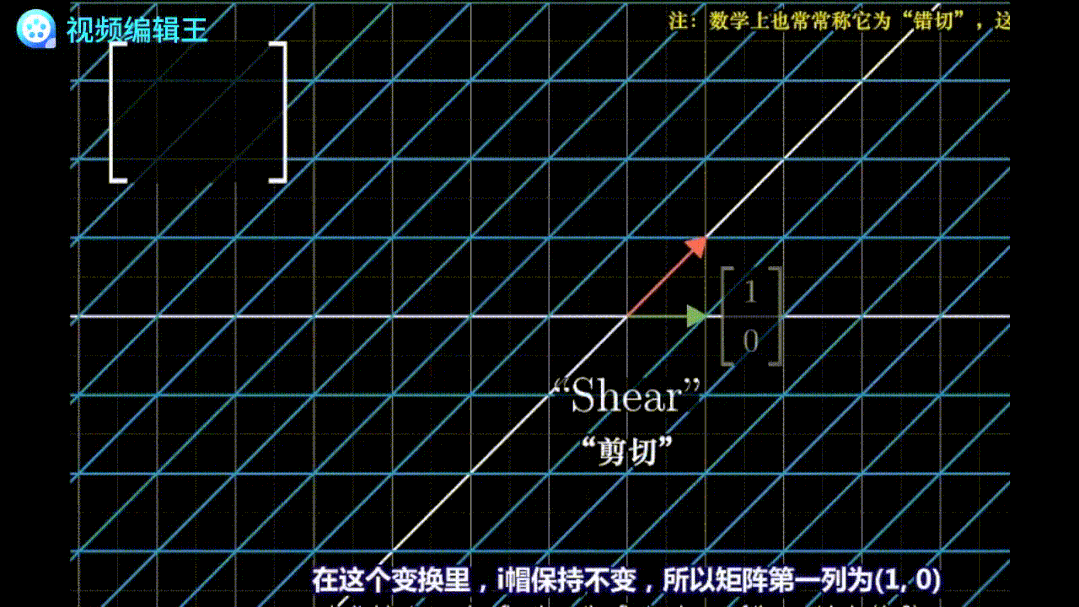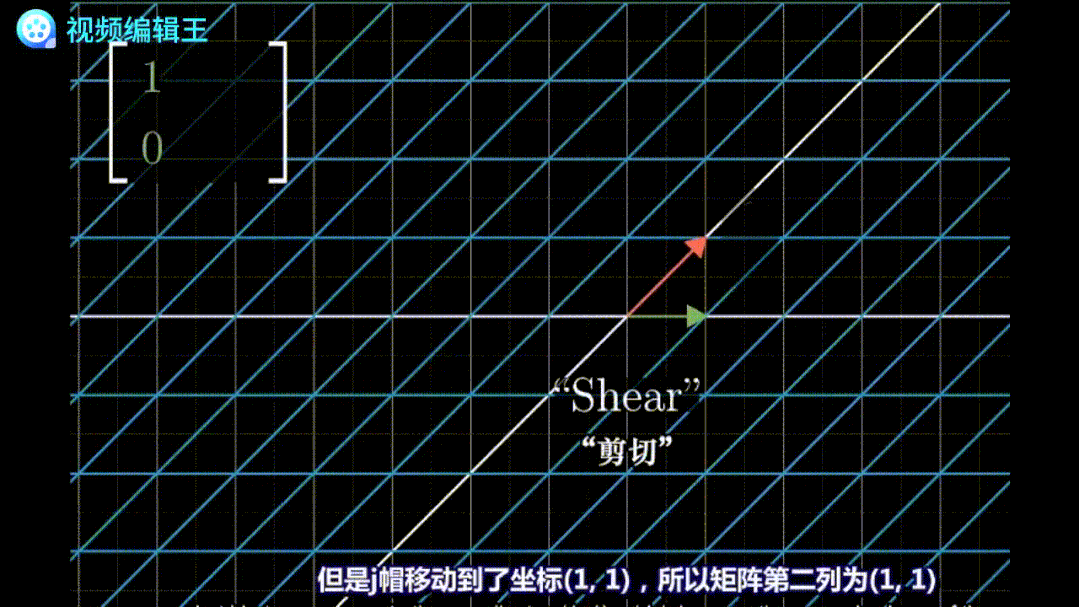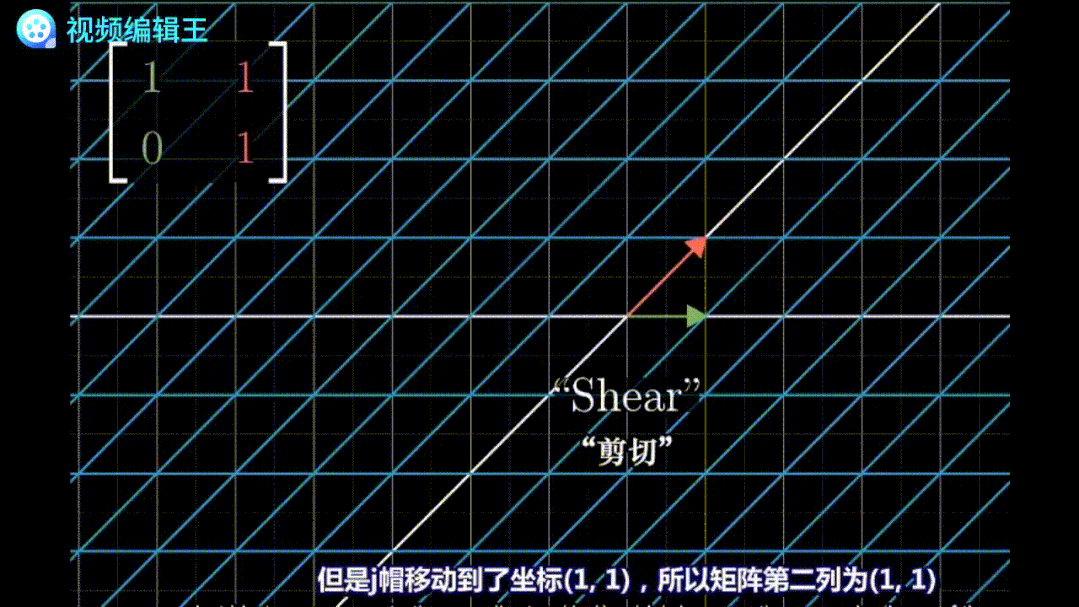
理解了上面的线性变换和矩阵的几何意义后,矩阵向量乘法就能一眼看穿了。
 矩阵向量乘法可以理解为:一个向量经过线性变换后的结果。乘法左边的矩阵代表变换信息,乘法右边的矩阵代表输出的信息,类似于函数f(x)。只要用几何变换的思想去看,就自然到不知道如何解释了...
矩阵向量乘法可以理解为:一个向量经过线性变换后的结果。乘法左边的矩阵代表变换信息,乘法右边的矩阵代表输出的信息,类似于函数f(x)。只要用几何变换的思想去看,就自然到不知道如何解释了...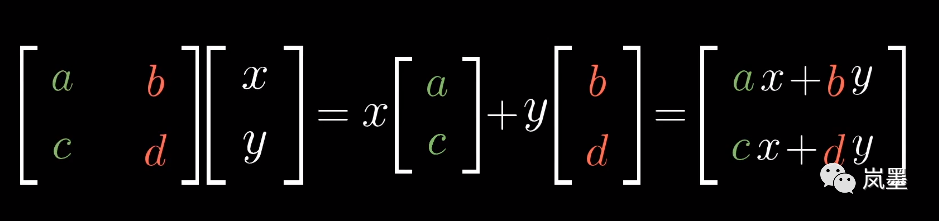
将一个二维平面逆时针旋转90°,再进行剪切,可以表示为如下的式子:用任意向量左乘旋转矩阵,再将得到的向量左乘剪切矩阵。这与复合函数的运算规则类似:F[g(x)]先将自变量x经过函数g处理,再将结果放入函数F中处理。
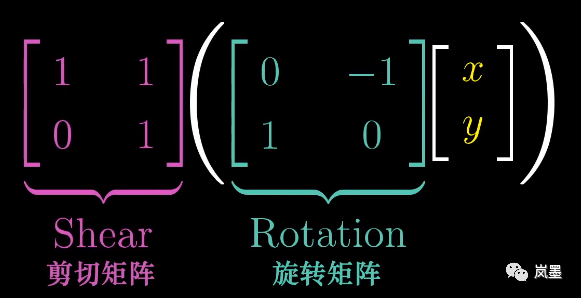
上面的两步,明显可以用一步来代替。这个新的矩阵,就可以称为线性变换复合。就像一个人往前走了两步,往后退了一步,可以用往前走了一步来代替总体效果。

上面的线性变换复合,就可以写成两个矩阵的乘积了。
矩阵乘积的几何意义:两个线性变换的复合作用。
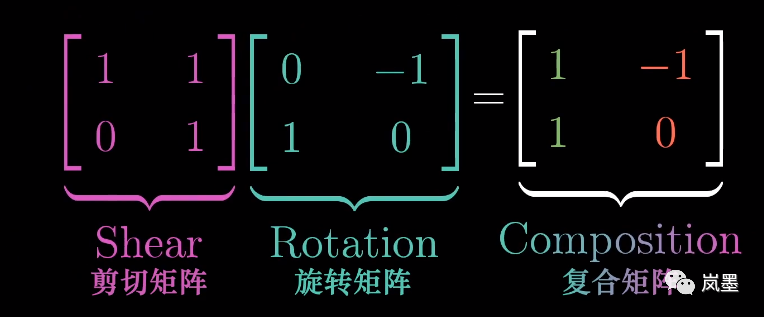
从几何的角度来欣赏矩阵乘积公式,也就非常容易了,只要找到两个基底的去向,就可以描述整个线性变换复合:
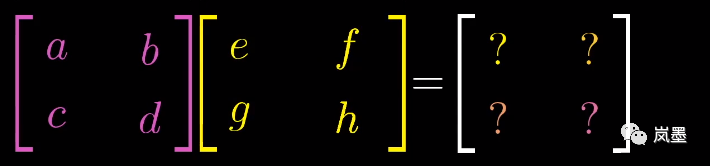 首先,基底i[1, 0]经过旋转矩阵,变换到了[e, g]。接下去基底i[e, g]经过剪切矩阵,变换为:
首先,基底i[1, 0]经过旋转矩阵,变换到了[e, g]。接下去基底i[e, g]经过剪切矩阵,变换为: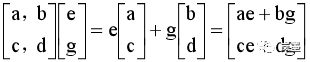 同样的,基底j[0, 1]经过旋转矩阵,变换到了[f, h]。接着基底j[f, h]经过剪切矩阵,变换为:
同样的,基底j[0, 1]经过旋转矩阵,变换到了[f, h]。接着基底j[f, h]经过剪切矩阵,变换为: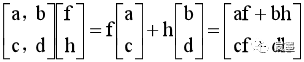 得到了两个基底的去向,就可以描述整个线性变换复合了:
得到了两个基底的去向,就可以描述整个线性变换复合了: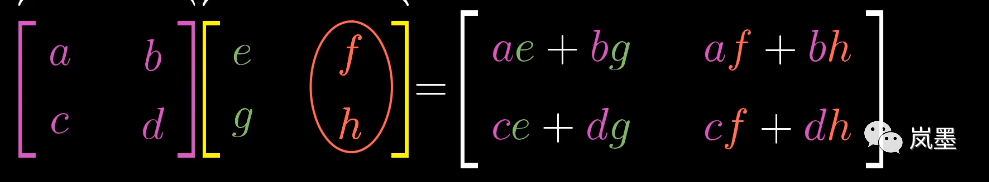 对比一下教材上的天书,从几何角度理解真的太舒服了...
对比一下教材上的天书,从几何角度理解真的太舒服了...
行列式用来测量线性变换后的空间被缩放的程度。
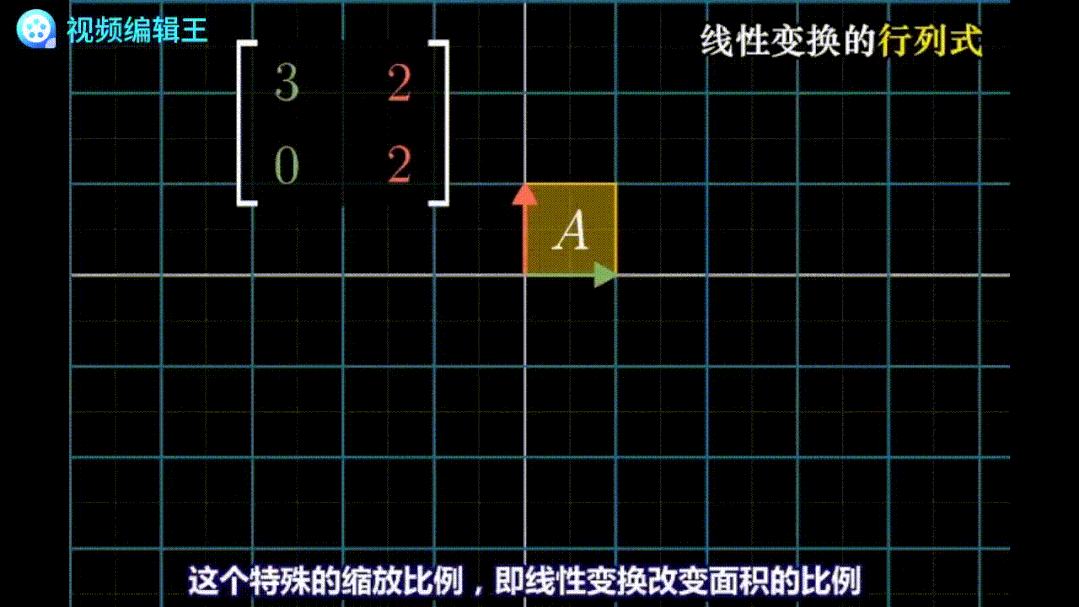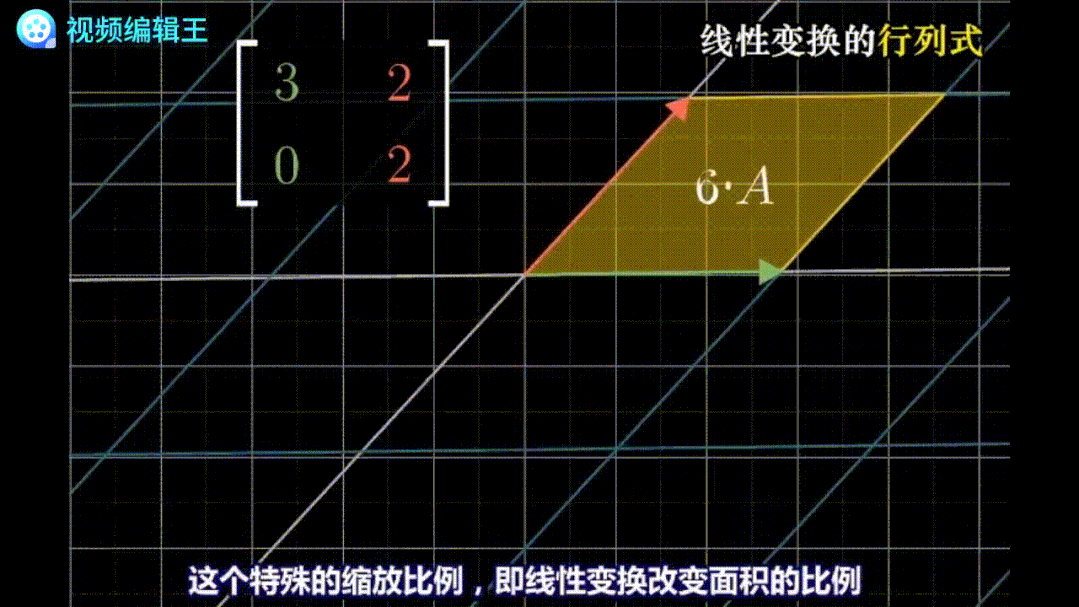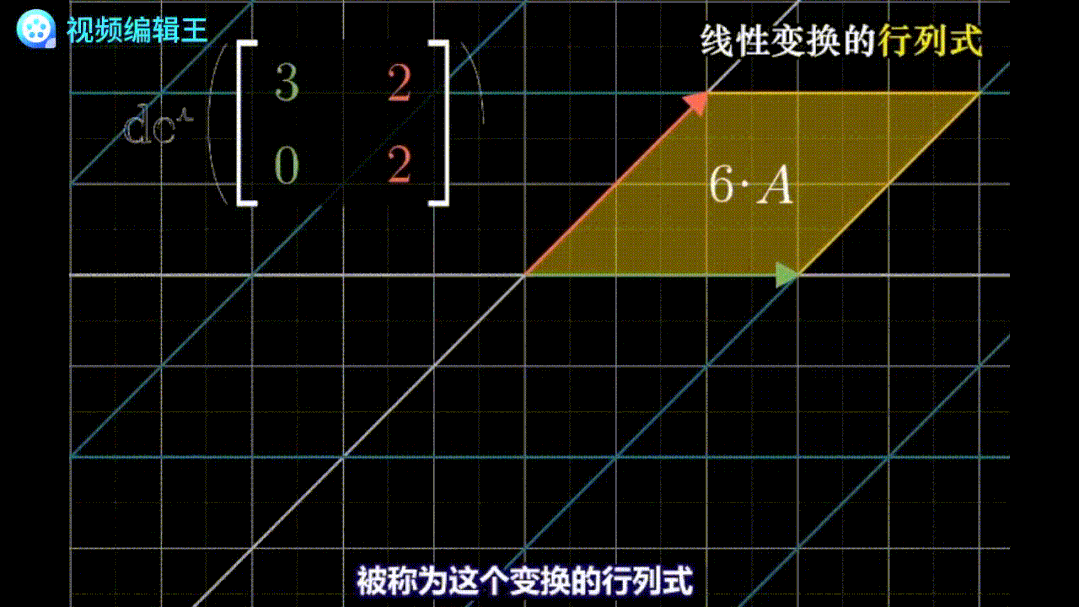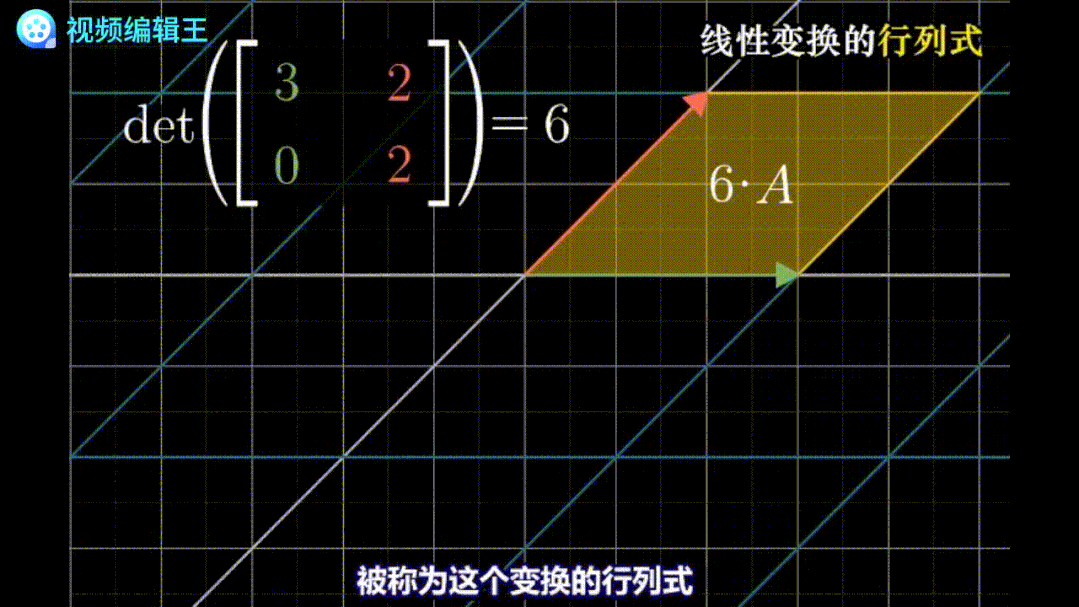
例如在二维空间,由于线性变换保持网格线平行且等距分布,所以只要知道基底向量构成的面积,在变换前后的比例,就能推算出任意空间在变换后的面积。三维空间中,行列式就代表体积的变化比例。
行列式为负,代表面积计算的方向发生了改变,像一张纸从背面看出来一样。行列式为零,意味着空间的维度下降了。二维空间面积为零,说明平面变成了点或线;三维空间体积为零,说明空间被压缩成了平面或者点线。从这个方向来理解行列式公式,也就比较容易了:
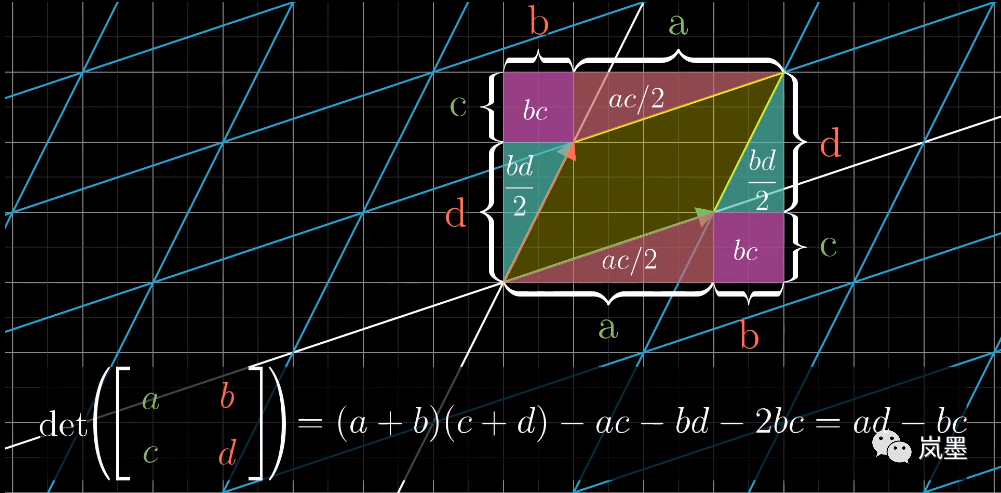
先截个图:
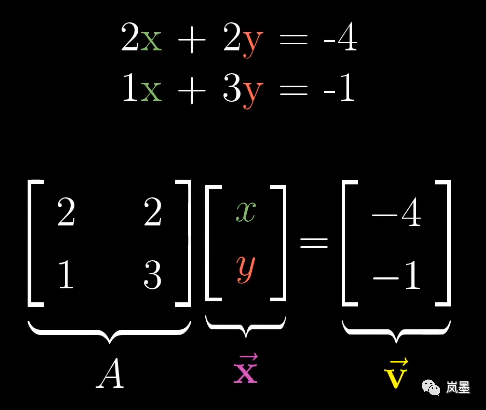
线性方程组:一个向量经过某种线性变换,把这个过程写成方程组的形式。把左边线性方程组中的系数项、未知数分别写成一个矩阵,组合为矩阵与向量的乘积,就能了解这个线性方程组的几何意义了。
为了求这个变换中的原始向量[x, y],我们可以把这个变换倒放一遍:
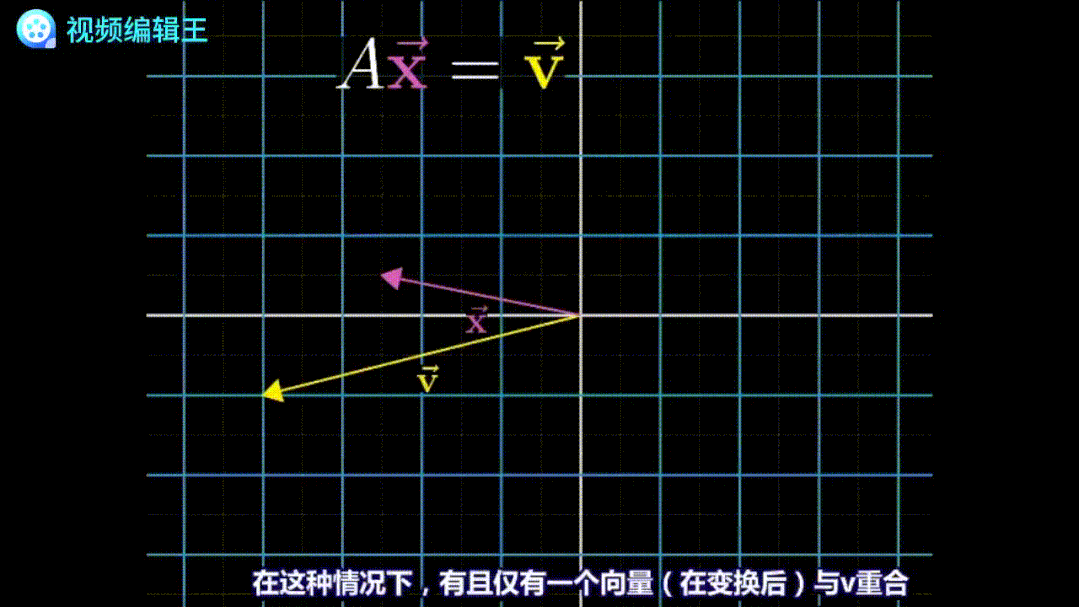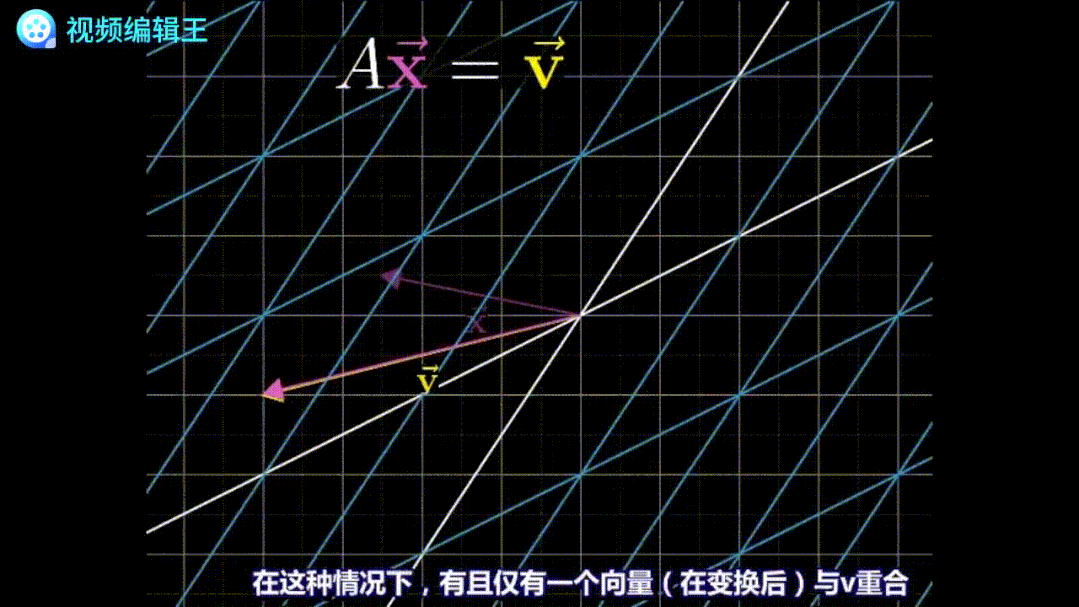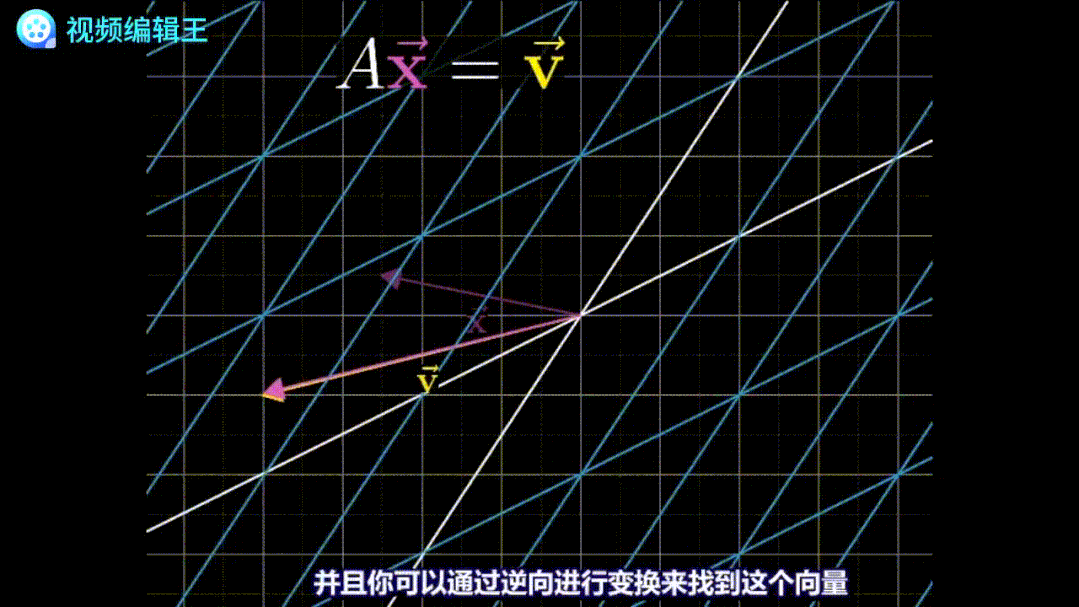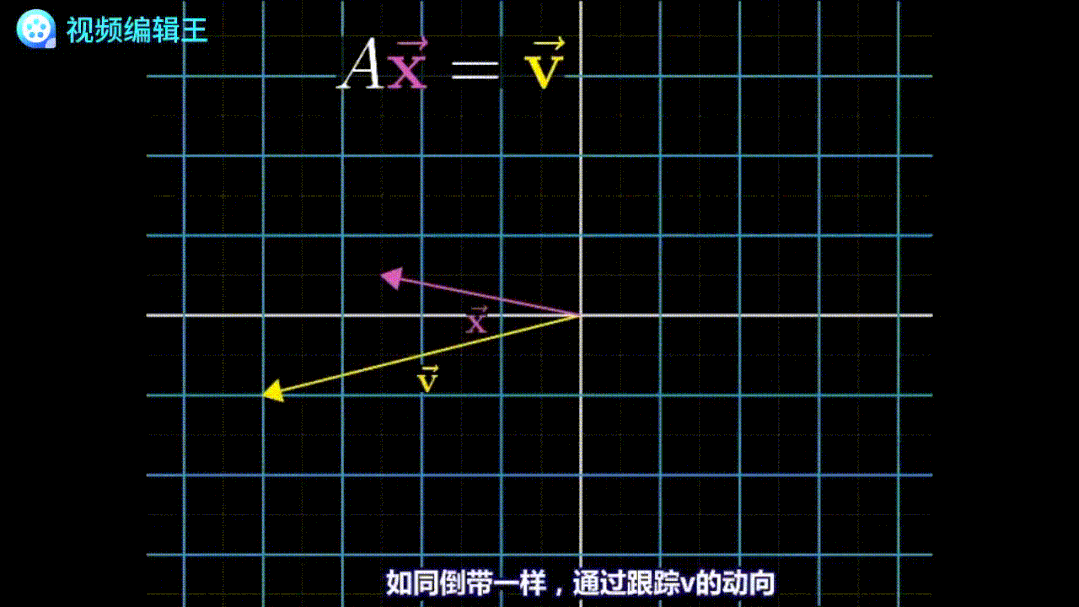
倒放过程中,原先的线性变换也会被反过来。这个反过来的变换,就叫逆矩阵。比如逆时针旋转90°的变换,它的逆矩阵就是顺时针旋转90°。很显然,两个互为逆矩阵的矩阵相乘,几何意义就是“啥也不做”:

现在再来解线性方程组,只要两边同时乘上A的逆矩阵,即把整个变换还原,就可以找到原始向量[x, y]。这里还有另一种情况:当线性变换A把二维平面压缩到了一维时(即A的行列式为零),这个线性方程组就无解了,因为我们无法把低纬度的东西,变换到高维度上。
教材上的定义非常严谨,但是看得让人脑壳疼...
 从几何方向来理解,矩阵的秩就是线性变换后空间的维度。例如2x2矩阵的最大秩是2,3x3矩阵的最大秩是3。若某个3x3矩阵的秩是2,说明这个矩阵代表的线性变换,将三维空间压缩到了二维平面。
从几何方向来理解,矩阵的秩就是线性变换后空间的维度。例如2x2矩阵的最大秩是2,3x3矩阵的最大秩是3。若某个3x3矩阵的秩是2,说明这个矩阵代表的线性变换,将三维空间压缩到了二维平面。同样的,从几何角度来理解特征向量,会变得非常舒坦。
以二维平面为例子,在一个线性变换中,有可能会出现这种情况:某个向量经过变换后,仍然在原先的直线上,仅仅是被拉伸或缩放了。

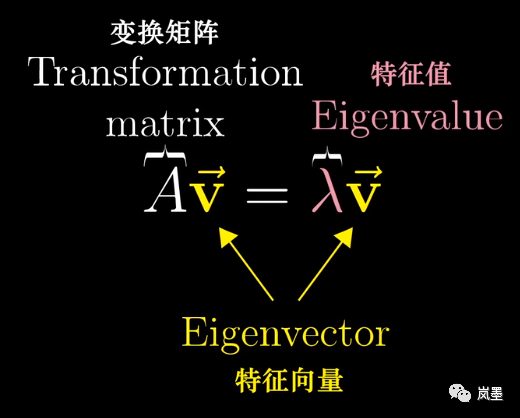
线性代数令人兴奋的地方在于,赋予了一种操控空间维度的方法。降维变换、旋转扭曲、压缩剪切..
真正的线性代数远不止这么点东西,也更深刻。
学呗。

评论
