CV岗位面试题:简述正则化与奥卡姆剃刀原则

文 | 七月在线
编 | 小七
解析:
正则化 Regularization
正则化最主要的功能是防止网络过拟合,主要有L1正则和L2正则:
L2正则化(岭回归)可能是最常用的正则化方法了,以通过惩罚目标函数中所有参数的平方来防止过拟合。即对于网络中的每个权重,在目标函数中增加一个项,其中是正则化惩罚系数。
加上后该式子关于梯度就是而不是了。L2正则化可以直观理解为它对于大数值的权重向量进行严厉惩罚,倾向于更加分散的权重向量。由于输入和权重之间的乘法操作,使网络更倾向于使用所有输入特征,而不是严重依赖输入特征中某些小部分特征。最后需要注意在梯度下降和参数更新的时候,使用L2正则化意味着所有的权重都以w += -lambda * W向着0线性下降。
L1正则化(套索回归)是另一个相对常用的正则化方法。对于每个我们都向目标函数增加一个项。L1和L2正则化也可以进行组合:,这也被称作弹性网络回归。L1正则化有一个有趣的性质,它会让权重向量在最优化的过程中变得稀疏(即非常接近0)。
也就是说,使用L1正则化的神经元最后使用的是它们最重要的输入数据的稀疏子集,同时对于噪音输入则几乎是不变的了。相较L1正则化,L2正则化中的权重向量大多是分散的小数字。在实践中,如果不是特别关注某些明确的特征选择,一般说来L2正则化都会比L1正则化效果好。
最大范式约束(Max norm constraints)是另一种形式的正则化,给每个神经元中权重向量的量级设定上限,并使用投影梯度下降来确保这一约束。在实践中,与之对应的是参数更新方式不变,然后要求神经元中的权重向量必须满足这一条件,一般值为3或者4。有研究者发文称在使用这种正则化方法时效果更好。这种正则化还有一个良好的性质,即使在学习率设置过高的时候,网络中也不会出现数值“爆炸”,这是因为它的参数更新始终是被限制着的。
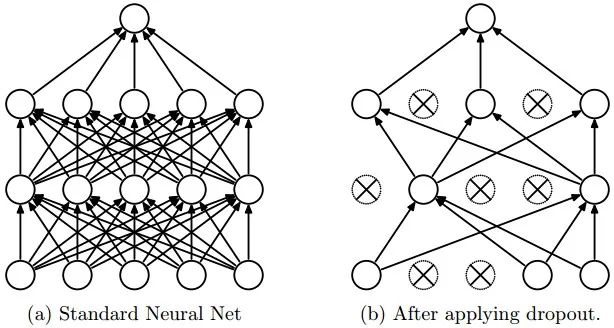
随机失活(Dropout)是一个简单又极其有效的正则化方法。该方法由Srivastava在论文Dropout: A Simple Way to Prevent Neural Networks from Overfitting中提出的,与L1正则化,L2正则化和最大范式约束等方法互为补充。在训练的时候,随机失活的实现方法是让神经元以超参数的概率被激活或者被设置为0。
图片展示了其核心思路:在训练过程中,随机失活可以被认为是对完整的神经网络抽样出一些子集,每次基于输入数据只更新子网络的参数(然而,数量巨大的子网络们并不是相互独立的,网络之间参数共享)。在推理阶段不使用随机失活,可以理解为是对数量巨大的子网络们做了模型集成(model ensemble),以此来计算出一个平均的预测。
奥卡姆剃刀原理:
这个原理称为"如无必要,勿增实体", 即"简单有效原理"。
奥卡姆剃刀原理是指,在科学研究任务中,应该优先使用较为简单的公式或者原理,而不是复杂的。应用到机器学习任务中,可以通过减小模型的复杂度来降低过拟合的风险,即模型在能够较好拟合训练集(经验风险)的前提下,尽量减小模型的复杂度(结构风险)。

评论