【机器学习基础】范数与正则化

前言

本文讨论了机器学习中正则化这个话题，对于L1正则项为什么稀疏也是面试中经常涉及的。

概要

正则化是机器学习中防止过拟合的一种重要技术。从数学上讲，它增加了一个正则化项，以防止系数如此完美地拟合而过度拟合。

为什么需要正则化

定义样本，为样本空间，模型函数，故预测值为，损失函数为。因此机器学习的训练过程可以转换为一个在泛函空间内，找到一个使得全局损失最小的模型，此时的损失函数又叫做「经验风险」（empirical risk），即损失函数的期望：

但上述损失函数只考虑了训练集上的经验风险，会出现过拟合的现象。为什么会出现过拟合？因为「模型参数过多或者结构过于复杂」。故我们需要一个函数来「描述模型的复杂程度」，即，也就是机器学习中常说到的「正则化项」（regularizer）。为了对抗过拟合，我们需要结合损失函数和正则化项，使他们的和最小，就可以将经验风险最小化问题转化为结构风险最小化，即机器学习中定义的「目标函数」（objective function）：

其中，目标函数，用于控制正则项的参数。若模型过度复杂使得更小，但正则化项却更大，总体的目标函数值不一定会降低。所以，总结来说，「正则化项起到了平衡偏差与方差的作用」。

以上便是以机器学习的角度，来讲述为什么需要正则化。总的来说主要是在原有的损失中加入描述模型复杂度的项，将经验风险（损失函数）转化为结构风险（目标函数），「综合考虑模型预测与真实的差距和模型复杂度」，以达到抑制过拟合的作用。接下来将具体的讲述范数与正则化的关系。

范数

一般来说，「损失函数是一个具有下确界的函数」，当预测值与真实值足够接近时，则损失值也会越接近下确界，这保证我们可以求出模型的最优解。当我们加入正则化项，变成目标函数，则也需要能够进行最优化求解。这也就要求「正则化项也应该是一个具有下确界的函数」，而范数则很好的满足了这个条件。

❝

范数（norm）：是具有“长度”概念的函数。简单来说，就是将向量投影到的值。

❞

我们假设某向量为，范数满足长度的三条基本性质：

• 非负性：；
• 齐次性：
• 三角不等式：

因此，范数也是一个具有下确界的函数，这是由「非负性和齐次性」所保证的。这一特性使得-范数天然适合做正则项，因为目标函数仍可用梯度下降等方式求解最优化问题。-范数作为正则项时被称为-正则项。

❝

范数的非负性保证了范数有下界。当齐次性等式中的取零时可知，零向量的范数是零，这保证了范数有下确界。

❞

-范数定义如下：

其中，应用较多的是范数（Taxicab distance，也称曼哈顿距离）、范数（欧几里得距离）。两者的区别，简单用一幅曼哈顿街道图来说明：

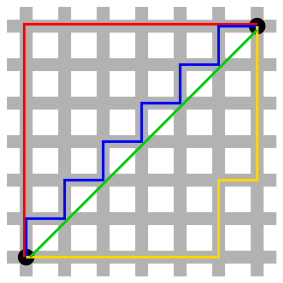
范数对应的是两点之间的移动，有多个解，而范数是欧几里得距离，关于如何最快到达两点之间总是有一个正确答案。

接下来介绍范数对应的正则化项，首先从正则化开始。

正则化项

以下对进行描述。其中，这里讨论的稀疏性只从最能理解的【导数的角度】进行解释。当然最为常见的应该是从优化的角度，还有一种是从概率论的角度（正则项相当于为加入拉普拉斯分布的先验，正则项相当于加入高斯分布的先验），具体见[3]。

正则化

我们简单定义一个线性模型：

其中，为样本的个数，为特征的个数，。

当训练集中存在统计噪声时（这里我们假设一种可能会发生过拟合的条件），冗余的特征可能会成为过拟合的来源。

❝

统计噪声：指的是某些特征为统计特征，如均值、求和、标准差等。它们加入在特征中，会在一定程度上加快模型的收敛，但它们也同样可以在一个线性模型中得到，对于统计噪声，模型无法从有效特征当中提取信息进行拟合，故而会转向冗余特征。

❞

为了对抗过拟合，如上述所说，我们可以通过降低模型的复杂度。最简单的方法就是令某些学习到的特征参数为0，即。因此，可以引入-范数。

❝

-范数：指的是向量中不为0的个数。

❞

-正则项为：

通过引入-正则项，则对原优化过程加入了一种我们常说的「惩罚机制」：当优化算法希望增加模型复杂度（此处特指将原来为零的参数更新为非零的情形）以降低模型的经验风险（即降低损失函数的）时，在结构风险上进行大小为（因为增加了1个非零参数）。由于结构风险（目标函数）是综合考虑损失函数和正则化项，「若当增加模型复杂度在经验风险的收益不足时，则结构化风险依旧会上升，而此时优化算法也会拒绝此更新」。

引入-正则化项会使模型参数稀疏化，使得模型易于解释。但是正常机器学习中并不使用-正则化项，因为它有无法避免的问题：非连续、非凸、不可微。所以，我们引入了-范数。

正则项

-正则项（亦称LASSO-正则项）为：

目标函数为：

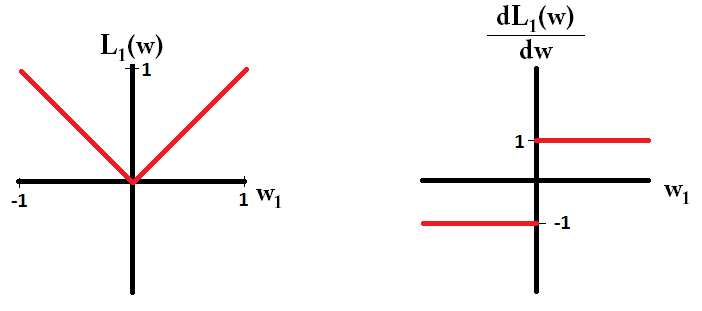
我们对目标函数进行对求偏导，计算其梯度：

❝

sgn：符号函数，

❞

如下图所示【简单起见，仅有一个参数组成】：

故参数更新为：

可以观察最后项，我们发现它始终让（，为负，，为正），因此L1正则化将「以相同的步长」（注意这里）将任何权重移向0，而不管权重的值是多少。所以可以「实现参数稀疏化」。

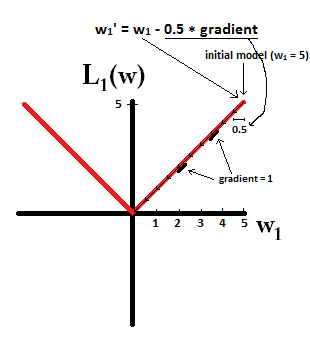
对于上图，我们忽略原损失函数对参数的梯度，当，，迭代多次，发现最终。

所以正则项的特点是：

• 不容易计算,在零点连续但不可导,需要分段求导；
• L1可以将一些权值缩小到零（稀疏），所以是一个天然的「特征选择器」；
• 由于它可以提供稀疏的解决方案，因此通常是「建模特征数量巨大时的首选正则项」。在这种情况下，获得稀疏解决方案具有很大的计算优势,因为可以简单地忽略具有零系数的特征。它任意选择高度相关的特征中的任何一个，并将其余特征对应的系数减少到零。
• L1范数函数对异常值更具抵抗力。

正则项

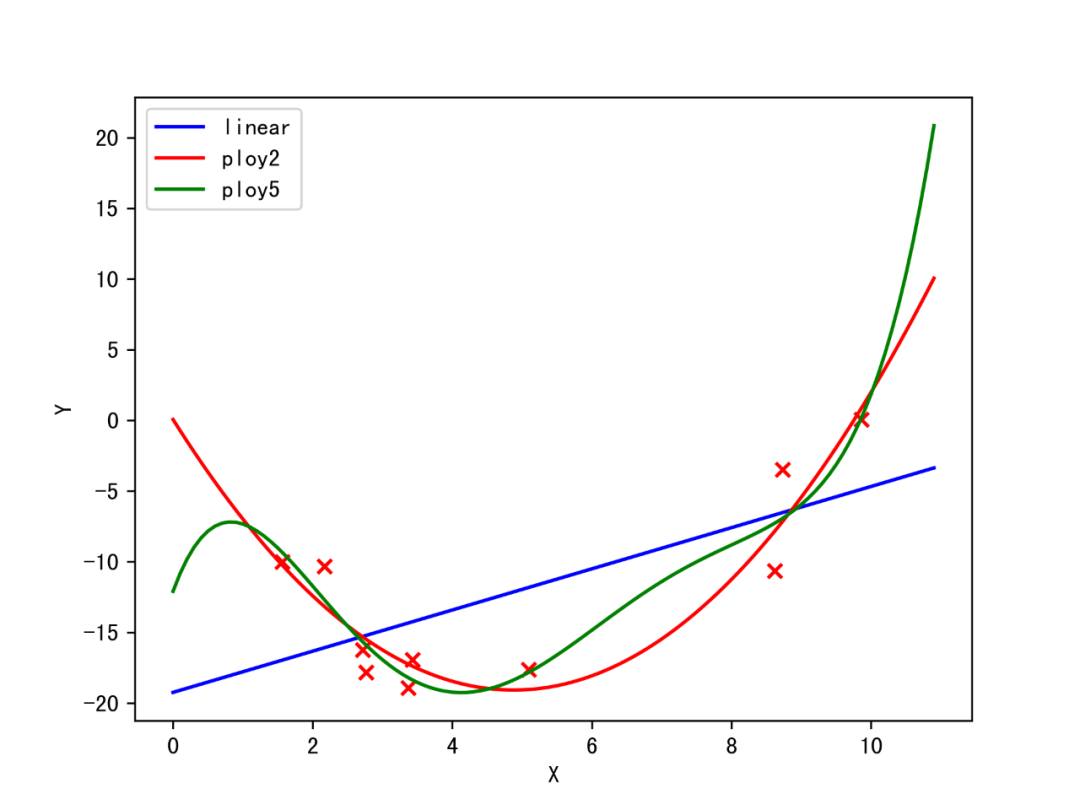
如上图所示，我们发现，当模型发生过拟合时，模型相对于其他模型，曲线函数更加的弯曲，这说明在「局部弯曲的部分，切线斜率特别大」，（即模型导数的绝对值特别大），对于整个模型来说，我们可以理解为所有的参数的绝对值之和特别大【梯度计算】。因此，如果我们有办法「使得这些参数的值，比较稠密均匀地集中在零附近」，就能有效地抑制过拟合。于是，便引入了范数。

-正则项为：

目标函数为：

对求偏导：

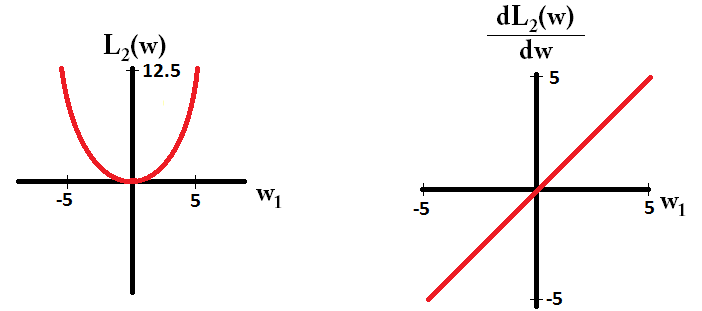
故参数更新为：

我们可以通过调整学习率和正则化参数，使得为0～1之间的数，从而衰减的权重，所有的参数接近于0，从而抑制过拟合。

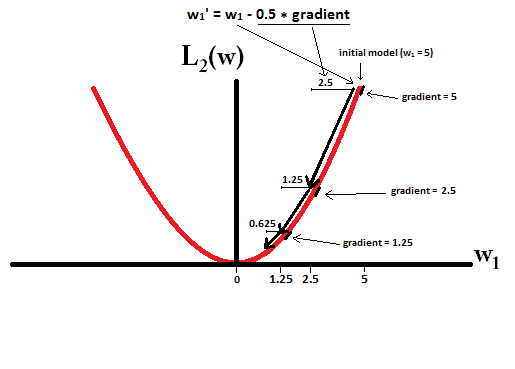
如上图所示，解释了为什么不会像那样产生稀疏解，而只是让权值接近0（当权值接近0时，它会采取越来越小的步骤）。

正则项的特点是：

• 容易计算，可导，适合基于梯度的方法将一些权值缩小到接近0；
• 相关的预测特征对应的系数值相似当特征的数量巨大时，计算量会比较大；
• 对outliers(异常值)非常敏感；
• 相对于L1正则化会更加精确；

参考资料

[1] https://www.kaggle.com/residentmario/l1-norms-versus-l2-norms

[2] https://stats.stackexchange.com/questions/45643/why-l1-norm-for-sparse-models

[3] https://www.zhihu.com/question/37096933/answer/475278057

往期精彩回顾




适合初学者入门人工智能的路线及资料下载
机器学习及深度学习笔记等资料打印
机器学习在线手册
深度学习笔记专辑
《统计学习方法》的代码复现专辑
AI基础下载
机器学习的数学基础专辑
本站qq群851320808，加入微信群请扫码：