来聊聊几种数据压缩算法
前言
当我们数据量大的时候，离不开数据压缩技术，不管是大数据量的传输和存储不进行压缩处理都会带来很大的挑战。例如我们常见的文件压缩包，几个G的文件可能经过压缩就只有几百M，可以为我们节省几倍甚至十几倍的空间，让我们硬盘能存储更多文件，带来了极大的便利和成本节约。
在项目开发上，当遇到文件传输或者一些大数据传输的时候就需要使用到数据压缩技术了，数据包得到成倍的减少，意味着我们同样的带宽、同样的磁盘可以更快处理更多的数据包。今天就来聊聊下面5种数据压缩算法的原理、实现以及性能测试。
- Deflate
- GZIP
- LZO
- LZ4
- Snappy
以上压缩算法底层实现大多基于LZ77算法和Huffman编码，咱们先来看看这两种算法的原理。
LZ77算法
如果文件中有两块内容相同，那么只要知道前一块的位置和大小，我们就可以确定后一块的内容，我们可以用（两者之间的距离，相同内容的长度）这样的信息来替换后一块内容。由于（两者之间的距离，相同内容的长度）这一信息的大小小于被替换内容的大小，所以文件得到了压缩。例如有一个文件的内容如下：http://www.baidu.comhttp://www.qq.com其中有些部分的内容，前面已经出现过了，下面用()括起来的部分就是相同的部分：http://www.baidu.com (http://www.)qq(.com)我们使用 (两者之间的距离，相同内容的长度) 这样一对信息，来替换后一块内容：http://www.baidu.com (21,12).qq(18,4)
(21,11)中，21[是21，图片上写错了]为相同内容块与当前位置之间的距离，11为相同内容的长度，即是：http://www.的长度；(18,4)中，18为相同内容块与当前位置之间的距离，4为相同内容的长度，即是：.com的长度；由于（两者之间的距离，相同内容的长度）这一对信息的大小，小于被替换内容的大小，所以文件得到了压缩。通过以上例子可以了解到LZ77算法的基本实现核心，下面来深入理解一下。要理解这种算法，需要对3个关键词有所了解。前向缓冲区每次读取数据的时候，先把一部分数据预载入前向缓冲区。为移入滑动窗口做准备滑动窗口一旦数据通过缓冲区，那么它将移动到滑动窗口中，并变成字典的一部分。短语字典从字符序列S1...Sn，组成n个短语。比如字符(A,B,D) ,可以组合的短语为{(A),(A,B),(A,B,D),(B),(B,D),(D)},如果这些字符在滑动窗口里面，就可以记为当前的短语字典，因为滑动窗口不断的向前滑动，所以短语字典也是不断的变化。LZ77的主要算法逻辑就是，先通过前向缓冲区预读数据，然后再向滑动窗口移入（滑动窗口有一定的长度），不断地寻找能与字典中短语匹配的最长短语，然后通过标记符标记。当压缩数据的时候，前向缓冲区与移动窗口之间在做短语匹配的是后会存在2种情况：找不到匹配时：将未匹配的符号编码成符号标记（多数都是字符本身）找到匹配时：将其最长的匹配编码成短语标记短语标记包含3个部分信息：滑动窗口中的偏移量（从匹配的地方开始计算）、匹配中的符号个数、匹配结束后的前向缓冲区的第一个符号。我们采用图例来看:1、开始
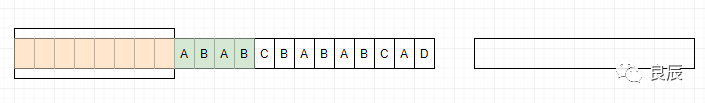2、滑动窗口中没有数据，所以没有匹配到短语，将字符A标记为A
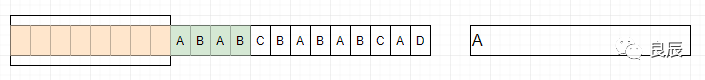3、滑动窗口中有A,没有从缓冲区中字符（BABC）中匹配到短语，依然把B标记为B
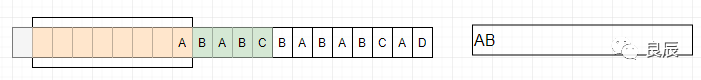4、缓冲区字符（ABCB）在滑动窗口的位移6位置找到AB,成功匹配到短语AB,将AB编码为(6,2,C)
5、缓冲区字符（BABA）在滑动窗口位移4的位置匹配到短语BAB,将BAB编码为(4,3,A)
6、缓冲区字符（BCAD）在滑动窗口位移2的位置匹配到短语BC，将BC编码为（2,2,A）
7、缓冲区字符D,在滑动窗口中没有找到匹配短语，标记为D
8、缓冲区中没有数据进入了，结束
解压类似于压缩的逆向过程，通过解码标记和保持滑动窗口中的符号来更新解压数据。· 当解码字符标记：将标记编码成字符拷贝到滑动窗口中· 解码短语标记：在滑动窗口中查找响应偏移量，同时找到指定长短的短语进行替换我们还是采用图例来看下:1、开始
2、符号标记A解码
3、符号标记B解码
4、短语标记(6,2,C)解码
5、短语标记(4,3,A)解码
6、短语标记(2,2,A)解码
7、符号标记D解码
大多数情况下LZ77压缩算法的压缩比相当高，当然了也和你选择滑动窗口大小，以及前向缓冲区大小有关系。其压缩过程是比较耗时的，因为要花费很多时间寻找滑动窗口中的短语匹配，不过解压过程会很快，因为每个标记都明确告知在哪个位置可以读取了。Huffman编码
是一种编码方式，哈夫曼编码是可变字长编码的一种，该方法完全依据字符出现概率来构造平均长度最短的码字。我们把文件中一定位长的值看作是符号，比如把8位长的256种值，也就是字节的256种值看作是符号。我们根据这些符号在文件中出现的频率，对这些符号重新编码。对于出现次数非常多的，我们用较少的位来表示，对于出现次数非常少的，我们用较多的位来表示。这样一来，文件的一些部分位数变少了，一些部分位数变多了，由于变小的部分比变大的部分多，整个文件的大小还是会减小，所以文件得到了压缩。要进行Huffman编码，首先要把整个文件读一遍，在读的过程中，统计每个符号（我们把字节的256种值看作是256种符号）的出现次数。然后根据符号的出现次数，建立Huffman树，通过Huffman树得到每个符号的新的编码。对于文件中出现次数较多的符号，它的Huffman编码的位数比较少。对于文件中出现次数较少的符号，它的Huffman编码的位数比较多。然后把文件中的每个字节替换成他们新的编码。哈夫曼树的构造1.根据给定的n个权值{w1,w2,…,wn}构成二叉树集合F={T1,T2,…,Tn},其中每棵二叉树Ti中只有一个带权为wi的根结点,其左右子树为空.2.在F中选取两棵根结点权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为左右子树根结点的权值之和.3.在F中删除这两棵树,同时将新的二叉树加入F中.4.重复2、3,直到F只含有一棵树为止.(得到哈夫曼树)例子，有这样一个文件的内容如下：AAAAABBBBCCCDDEEFG我们统计一下各个符号的出现次数，A(5) B(4) C(3) D(2) E(2) F(1) G(1)建立Huffman树的过程如图：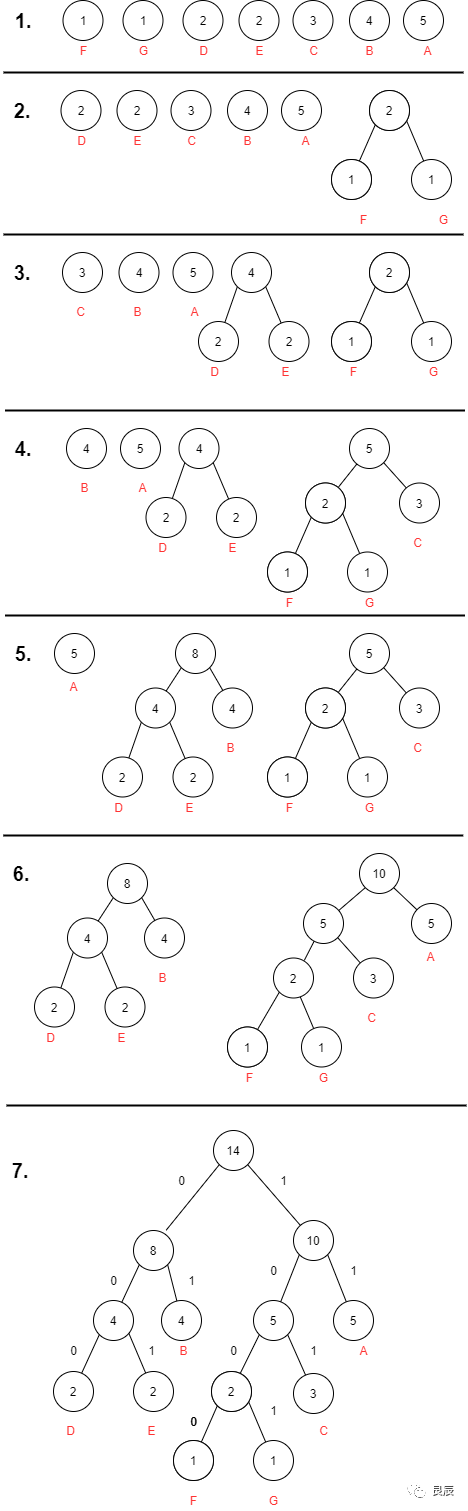
通过最终的Huffman树，我们可以得到每个符号的Huffman编码。A(5):11B(4):01C(3):101D(2):000E(2):001F(1):1000G(1):1001我们可以看到，Huffman树的建立方法就保证了，出现次数多的符号，得到的Huffman编码位数少，出现次数少的符号，得到的Huffman编码位数多。各个符号的Huffman编码的长度不一，也就是变长编码。对于变长编码，可能会遇到一个问题，就是重新编码的文件中可能会无法如区分这些编码。比如，a的编码为000，b的编码为0001，c的编码为1，那么当遇到0001时，就不知道0001代表ac，还是代表b。出现这种问题的原因是a的编码是b的编码的前缀。由于Huffman编码为根结点到叶子结点路径上的0和1的序列，而一个叶子结点的路径不可能是另一个叶子结点路径的前缀，所以一个Huffman编码不可能为另一个Huffman编码的前缀，这就保证了Huffman编码是可以区分的。算法实现和性能测试
这里直接宣布结果，详情可以看我的这篇文章：5种数据压缩算法实现和性能测试以514KB大小的JSON字符串测试为例：Benchmark Mode Samples Mean Mean error Units
o.s.MyBenchmark.testDeflateCompress avgt 10 12.100 0.498 ms/op
o.s.MyBenchmark.testGzipCompress avgt 10 7.434 4.398 ms/op
o.s.MyBenchmark.testLz4Compress avgt 10 3.310 1.096 ms/op
o.s.MyBenchmark.testLzoCompress avgt 10 3.255 1.014 ms/op
o.s.MyBenchmark.testSnappyCompress avgt 10 1.971 0.209 ms/op
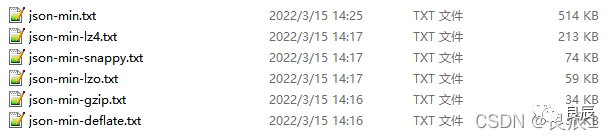
- 压缩耗时：snappy(1.9) < lzo(3.2) < lz4(3.3) < gzip(7.4) < deflate(12.1)，如果数据比较大，lzo的速度比deflate还慢
- 压缩率(越小越好)：deflate(3.3%) < gzip(3.8%) < lzo(8.4%) < snappy(11.5%) < lz4(47.3%)
- deflate压缩耗时最大，但压缩率最好，gzip相对deflate综合性能更好，压缩率相差不多但压缩时间几乎少一半，综合性能最好的要算snappy，它是最快的，压缩率也挺不错，追求速度可以选择它，lzo和lz4综合性能较差，不推荐使用
评论