经典分类:线性判别分析模型!
这几天看了看SVM的推导,看的是真的头疼,那就先梳理基础的线性判别分析模型,加深对SVM的理解。
线性判别分析是一种线性的分类模型。
线性分类模型是指采用直线(或超平面)将样本直接划开的模型,其形式可以表示成 的形式,划分平面可以表示成 。这里可以看出,线性分类模型对于样本的拟合并不一定是线性的,例如逻辑回归(外面套了一层sigmod函数)和感知机(外面套了一层激活函数)。
线性判别分析的基本思想是把所有样本投影到一条直线上,使样本在这条直线上最容易分类。
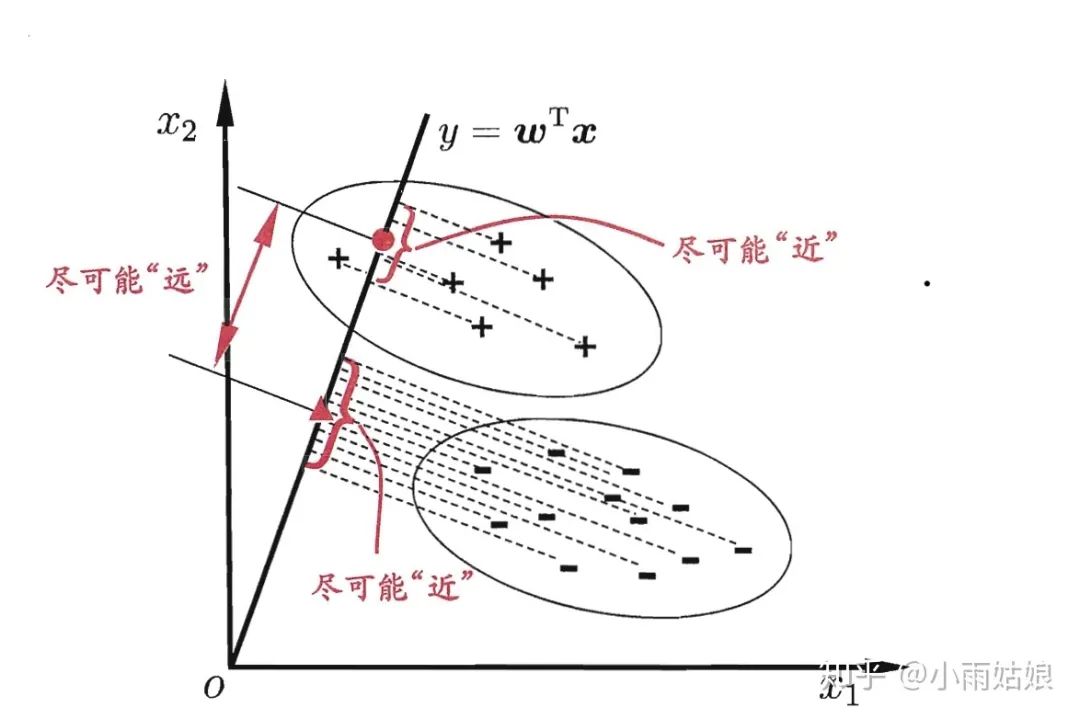
设直线的方向向量为,则样本在直线上的投影为,如图:

我们的目标是使两类样本的中心点在线上的投影距离大(两类样本区分度高),同时使每一类样本在线上投影的离散程度尽可能小(类内样本区分度低)。
令,,分别代表每一类的样本,每一类样本的均值向量,每一类样本的协方差矩阵。
若将所有样本都投影到直线上,则两类样本的中心点可分别表示为, 。
若将所有样本都投影到直线上,则两类样本的协方差可表示为, 。
协方差是什么?协方差表示的是两个变量总体误差的期望。如果两个变量的变化趋势一致,则为正值;若相反则为负值;变化趋势无关时为0,此时两个变量独立。

协方差矩阵是什么?协方差矩阵的元素是任意两个变量之间的协方差。
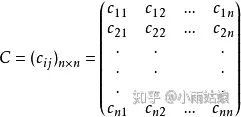
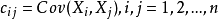
因此我们如果要让两类样本在投影后离散程度尽可能小,我们就应该让他们之间的方差尽可能小。计算每一类元素投影后的方差在做向量化时,中间就是协方差矩阵(不好意思,下面第二个应该加个转置)。
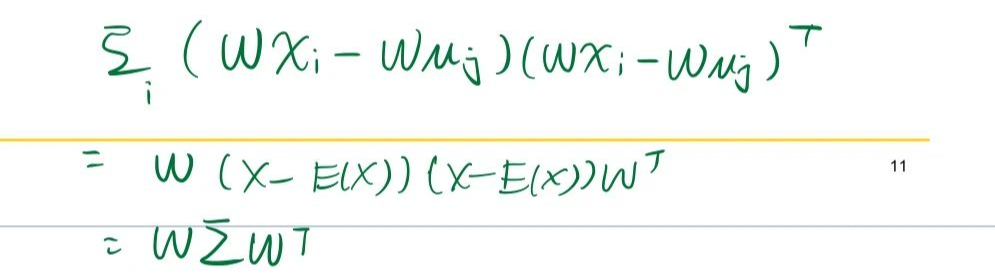
使两类样本的中心点在线上的投影距离大,同时使每一类样本在线上投影的离散程度尽可能小的表达式可以写为:
对于参数的优化问题可以做如下转换:
因为求的是一个方向向量,所以 同样也是所求的解,因此我们可以假定
则问题转换为二次规划问题:
解得:
最后的判别模型可表示为:
其中b由于不在目标函数中,所以要手动去找,一般经验方法是:
Python实现如下:
import numpy as np
# 2 dm vectors
x_0 = np.array([[2.95,6.63],[2.53,7.79],[3.57,5.65],[3.16,5.47]])
x_1 = np.array([[2.58,4.46],[2.16,6.22],[3.27,3.52]])
# mean vectors
u_0 = np.mean(x_0, axis=0)
u_1 = np.mean(x_1, axis=0)
# S_w & S_b
S_w = np.cov(x_0, rowvar=False) + np.cov(x_1, rowvar=False)
S_b = np.matmul((u_0 - u_1).reshape(-1,1), (u_0 - u_1).reshape(1,-1))
# Result
w = np.matmul(np.linalg.inv(S_w), (u_0 - u_1))
b = -1 * np.dot((u_0+u_1)/2, w)
实验结果:
利用 LDA 进行一个分类的问题:假设一个产品有两个参数柔软性 A 和钢性 B,来衡量它是否合格,如下图所示:
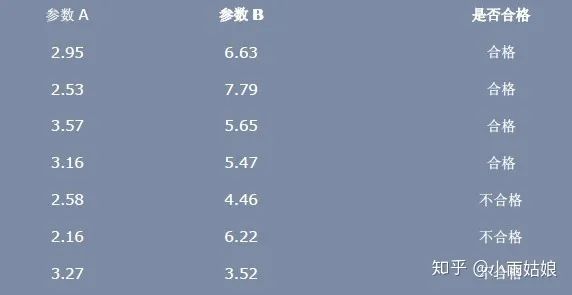
X_0类:
for i in x_0:
print(np.dot(w , i) + b)
# 7.908179218783431
# 8.836977507881144
# 11.047547831774281
# 3.8717837839741094
X_1类:
for i in x_1:
print(np.dot(i , x_0[0]) + b)
# -39.39697440389426
# -28.96717440389427
# -43.59367440389427