算法实战Array类型题目(二)
算法实战Array类型题目
这些题目又很多解法,个人只是针对不同得数据类型进行解答:
1. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:

示例 2:

对于这种题目,第一眼我也是懵逼的,也许你会在纸上列举n从1到10的不同结果找规律,
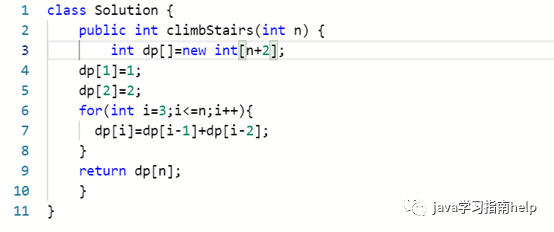
其实这题是斐波那契数列,公式 dp[n] = dp[n-1] + dp[n-2]dp[n]=dp[n−1]+dp[n−2]。
因为你想爬上第n个台阶其实可以分为两个步骤:
1.爬上 n-1 阶楼梯的方法数量。因为再爬1阶就能到第n阶
2.爬上 n-2 阶楼梯的方法数量,因为再爬2阶就能到第n阶
你可能会想,这么考虑会不会遗漏,其实不会。
所以解题如下:
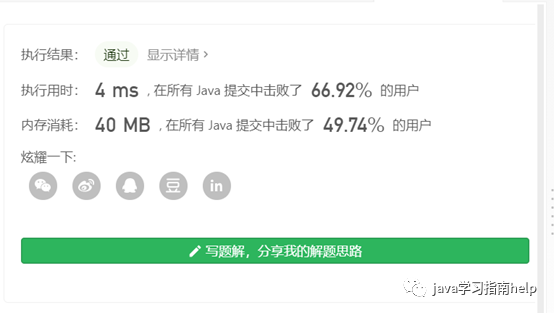
这是在leetcode上面的提交结果:
注意一点,每道题他有很多解法,这里是为了熟悉数组,我们用数组进行解答。
2. 盛最多水的容器
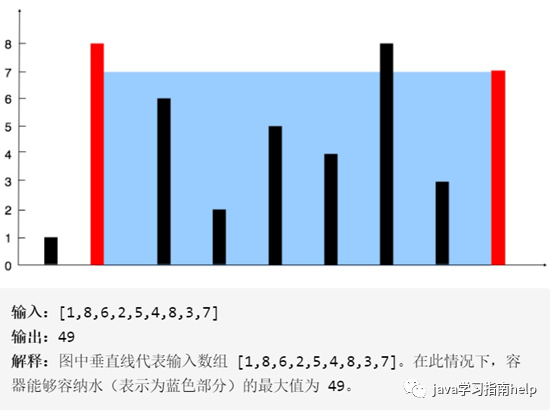
给你 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器。
示例 1:

这题目一开始的思路是暴力法,我们可以遍历数组从下标0一直遍历到数组最后,然后看不同情况下,另外一一个高度不断遍历,求出最大值。但是这种解法算出来的事件复杂度为n的平方。
这时候有个解决方案:
双指针法:
指针每一次移动,都意味着排除掉了一个柱子。
如下图所示我们一开始考虑最远的柱子所能容纳水的面积。水的宽度是两根柱子之间的距离 d = 8;水的高度取决于两根柱子之间较短的那个,即左边柱子的高度 h = 3。水的面积就是 3×8=24。
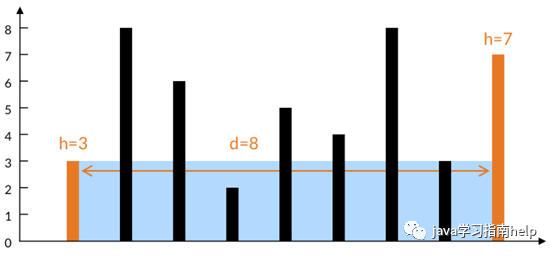
这个时候我们可以选择移动较小的0号柱子,为啥移动0号而不移动最右边的柱子,因为这个时候最右边的柱子比最左边的高,我们为了找到面积最大,高度被最左边的柱子高度控制住了,如果移动右边的柱子,那么高度可能不变或者更小,宽度是可定变小的,所以我们移动左边的柱子(高度较小的柱子)。每次的移动都是选择高度较小的柱子,因为宽度一直在变小。(这就是这题双指针方法的关键,每次移动的规则为高度小的柱子)然后把每次移动后算出的面积进行比较,最后得到最大的。
最后我们得出:
时间复杂度:O(N)O(N),双指针总计最多遍历整个数组一次。
空间复杂度:O(1)O(1),只需要额外的常数级别的空间。
这就是个人写的代码:
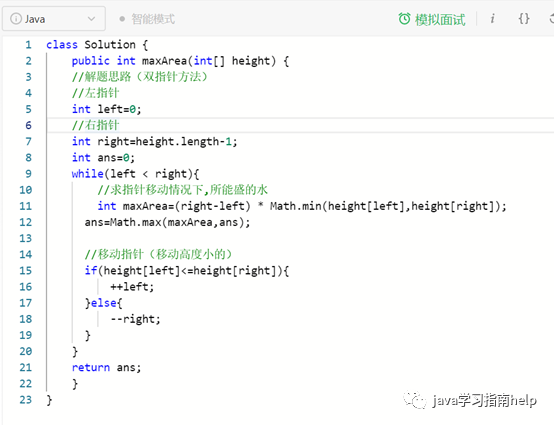
这是提交结果: