一道题目带你搞懂回溯算法
明天就过年了,无论你有没有回到家乡,都祝你新的一年,有所收获。
今天分享一道算法题,希望能让你学会回溯算法的思路。
学会了回溯,你就能解决著名的八皇后问题,数学家高斯穷其一生都没有解出八皇后的解,而借助现代计算机和回溯算法,你分分钟就搞定了,当然,N 皇后也不在话下。
回溯法(back tracking)是一种选优搜素算法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,当然,回溯也是暴力搜索法中的一种。
昨天看到一道回溯算法题目,非常烧脑,不过我很喜欢这种感觉,程序员应该定期刷一刷算法题,只有刷算法题目的时候,我才觉得那是真正意义上的编程,平时的工作在多数情况下,都是熟练调用编程语言或框架的 API 而已。
这道题目是 leetcode 第 93 题,难度为中等,让我们根据一个包含数字的字符串,复原它所有可能的 IP 地址。具体如下:
给定一个只包含数字的字符串,复原它并返回所有可能的 IP 地址格式。
有效的 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
例如:"0.1.2.201" 和 "192.168.1.1" 是有效的 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 是无效的 IP 地址。
示例 1:
输入:s = "25525511135"
输出:["255.255.11.135","255.255.111.35"]
示例 2:
输入:s = "0000"
输出:["0.0.0.0"]
示例 3:
输入:s = "1111"
输出:["1.1.1.1"]
示例 4:
输入:s = "010010"
输出:["0.10.0.10","0.100.1.0"]
示例 5:
输入:s = "101023"
输出:["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/restore-ip-addresses
暴力穷举
这个题目,我相信你大脑里最先想到的就是找三个点来分隔出 4 个字符串,然后判断分隔出的 4 个字符串是否满足 ip 某一段的要求,假如 4 个字符串都在 0 到 255 之间并且没有前导的零,那就是一个合法的 ip 地址。
但是三个点号的位置不太容易穷举,4 个字符串的长度倒是好穷举的,每个字符串的长度至少是 1,至多是 3,只有 3 种可能,,因此可以穷尽 4 个字符串的所有长度,也就是 3 的 4 次方 81 种可能。
如果 4 个字符串的长度加起来等于给定字符串的长度时,就可以按长度分隔,然后分别进行判断了。能想到这一点,就不难写出如下代码:
class Solution(object):
def restoreIpAddresses(self, s):
"""
:type s: str
:rtype: List[str]
"""
result = []
for a in range(1,4):
for b in range(1,4):
for c in range(1,4):
for d in range(1,4):
if a+b+c+d == len(s):
s1 = s[0:a]
s2 = s[a:a+b]
s3 = s[a+b:a+b+c]
s4 = s[-d:]
if self.isValid(s1) \
and self.isValid(s2) \
and self.isValid(s3) \
and self.isValid(s4):
result.append("{}.{}.{}.{}".format(s1,s2,s3,s4))
return result;
def isValid(self,s_sub):
if len(s_sub) > 1 and s_sub.startswith('0'):
return False
if int(s_sub) <= 255: #全部都由数字组成
return True
return False
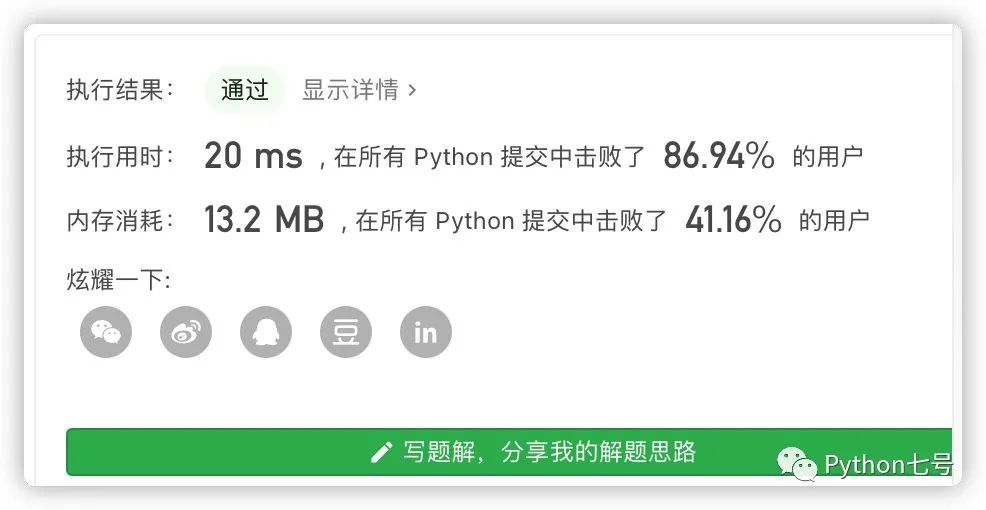
但这种方法非常易懂,但是却不够通用,无法举一反三,比如说题目改成 ipv6 的地址,这种方法就不太合适了。
回溯思想
接下来我们尝试一下回溯的思路。
比如 25525511135,先来确定 ip 的第一段,第一段最多有 3 种可能:2,25,255,这里可以使用一个小循环。假如先选择 2 做为 ip 的第一段,2 小于等于 255,满足要求。
接下来确定 ip 的第二段,也就是说对剩余的字符串 5525511135 重复上述操作,同样的,最多有 3 种可能:5,55,525。假如这里选择 5, 5 是小于等于 255 的,因此满足条件。
接下来确定 ip 的第三段。
接下来确定 ip 的第四段。
每一段的选择,都是同样的操作。这就很像是一个决策树,每做一次选择,都是沿着树的某一分支走到叶子节点的过程,我这里使用脑图来展示一下这个决策树。
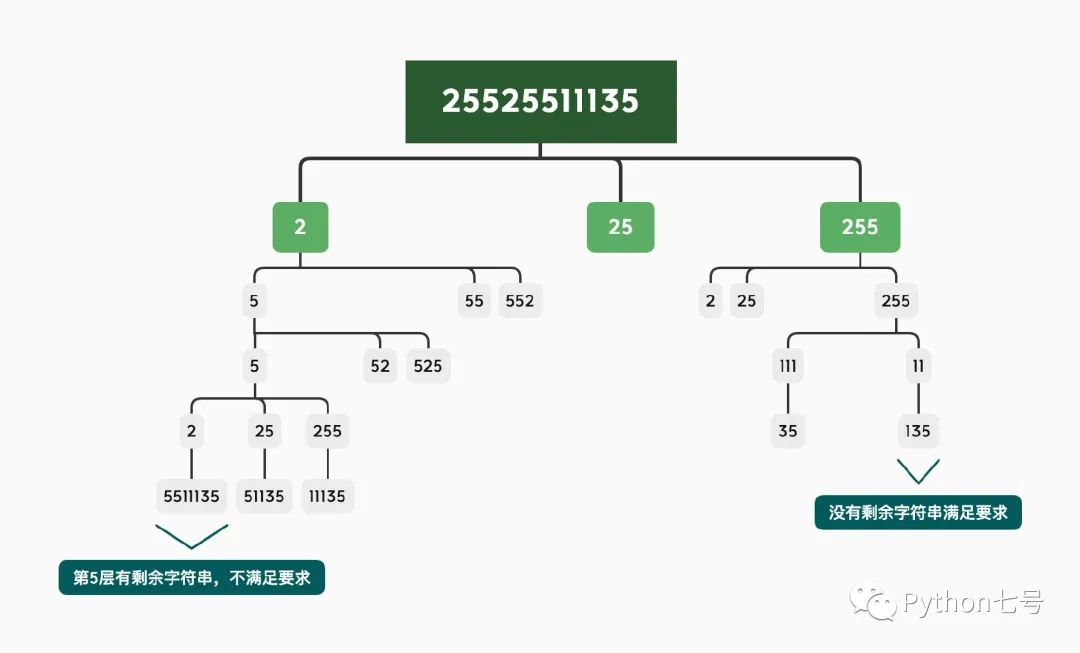
上图中除了叶子节点,其他节点都是 3 个子节点,某些我没有画出,希望不影响你理解。
每一层的检索都是一个递归操作,递归的退出条件就是到第 5 层结束,第 5 层结束后如果没有剩余字符串,说明找到了一个正确的 IP 地址,保存到结果集里即可。
不可避免地需要遍历这棵决策树的每个节点,比如 2.5.5.2,本质就是多叉树的遍历操作,这也就是回溯思想的核心。写代码时我们可以把多叉树的遍历骨架写出来:
def backtrace(root :str) -> None:
"""
有 3 个子节点的多叉树的中序遍历。
"""
if 满足退出条件:
if 满足要求:
加入结果集
退出
for i in range(0,3):
if i < len(root): #索引不能超过字符串的长度
#选择 root[0:i+1]
#具体做法就是 tmp_list.append(root[0:i+1])
backtrace(root[i+1:])
#撤销选择 root[0:i+1]
#具体做法就是 tmp_list.pop()
进入下一轮决策(递归)之前,先做选择,把当前 ip 段加入路径 tmp_list 中,决策(递归)完成后,再撤销选择。
这里有人可能不太理解,为什么需要撤销选择?其实不难理解,看上图决策树的最左边的分支,当遍历到 2.5.5.2 发现不合适的时候,需要回溯到 2.5.5,然后选择 25,也就是说最后的 2 加入 tmp_list 之后,判断不合适,递归返回之后,我们需要把 2 删除,然后腾出空间放 25,这也是为什么叫回溯算法的原因,遇到不符合目标的,就回头重新选择。当然了,遇到合适的,也要重新选择,是因为我们要选出所有合法的 ip 地址。
接下来,为这个骨架填充一点血肉。遍历了每个节点,需要把这些节点的顺序保存下来,这里使用一个 tmp_list 来保存,为了编写退出条件,还需要一个变量指示现在是第几层,为了返回最终结果,再传入一个 result 的数组来保存。
def backtrace(root :str, tmp_list:list, levle: int, result:list ) -> None:
"""
有 3 个子节点的多叉树的中序遍历。
tmp_list 保存遍历的路径,比如 2.5.5.2
level 表示现在是第几层,初始调用时传入 1
"""
##剩余字符串为空,或者遍历到第 5 层,终止递归。
if len(root) == 0 or level == 5:
##同时满足时,说明已经找到了合法的ip
if len(root) == 0 and level == 5:
result.append(".".join(tmp_list))
return
for i in range(0,3):
if i < len(root): #索引不能超过字符串的长度
#选择 root[0:i+1]
part = root[0:i+1]
if isValid(part):
#合法的部分,才去递归
#加入选择
tmp_list.append(part)
backtrace(root[i+1:],tmp_list,level+1,result)
#撤销选择
tmp_list.pop()
else:
pass
组装一下,以下是完整代码,可直接在 leetcode 运行的,提交后看看结果:
class Solution(object):
def restoreIpAddresses(self, s):
"""
:type s: str
:rtype: List[str]
"""
if len(s) < 4:
return []
result = []
tmp_list = []
self.backtrace(s,tmp_list,1,result);
return result
def backtrace(self, root:str , tmp_list:list, level:int, result:list) -> None:
"""
有 3 个子节点的多叉树的中序遍历。
tmp_list 保存遍历的路径,比如 2.5.5.2
level 表示现在是第几层,初始调用时传入 1
"""
if len(root) == 0 or level == 5:
if len(root) == 0 and level == 5:
result.append(".".join(tmp_list))
return
for i in range(0,3):
if i < len(root): #索引不能超过字符串的长度
#选择 root[0:i+1]
part = root[0:i+1]
if self.isValid(part):
#合法的部分,才去递归
#加入选择
tmp_list.append(part)
self.backtrace(root[i+1:],tmp_list,level+1,result)
#撤销选择
tmp_list.pop()
else:
pass
def isValid(self, sub_s : str) -> bool:
if len(sub_s) > 1 and sub_s.startswith('0'):
return False
if 0 <= int(sub_s) <= 255:
return True
return False
运行结果如下:
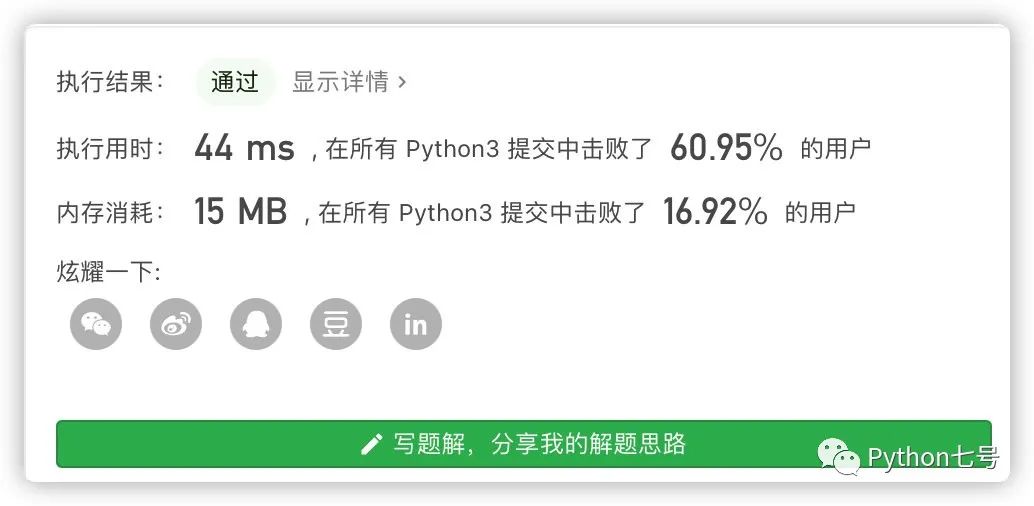
心心苦苦搞了半天,看来还没有第一段暴力解法来得快,别灰心,一定有什么可以优化的地方,其实,只要有某一段 ip 的长度大于 1,且是 0 开头的时候,后面就不需要向下递归了,可以提升点效率。
比如:输入:s = "010010",当 "01"做为第一段时就可以 break 跳出循环了。
优化一下 backtrace 函数和 isValid 函数:
def backtrace(self, root:str , tmp_list:list, level:int, result:list) -> None:
"""
有 3 个子节点的多叉树的中序遍历。
tmp_list 保存遍历的路径,比如 2.5.5.2
level 表示现在是第几层,初始调用时传入 1
"""
if len(root) == 0 or level == 5:
if len(root) == 0 and level == 5:
result.append(".".join(tmp_list))
return
for i in range(0,3):
if i < len(root): #索引不能超过字符串的长度
#选择 root[0:i+1]
part = root[0:i+1]
##如果某段以0开头,且长度超过 1 ,那么跳出循环,提升效率
if part.startswith('0') and len(part)>1:
break;
if self.isValid(part):
#合法的部分,才去递归
#加入选择
tmp_list.append(part)
self.backtrace(root[i+1:],tmp_list,level+1,result)
#撤销选择
tmp_list.pop()
else:
pass
def isValid(self, sub_s : str) -> bool:
# if len(sub_s) > 1 and sub_s.startswith('0'):
# return False
if int(sub_s) <= 255:
return True
return False
一个小小的优化,再次提交看结果,确实提升了不少: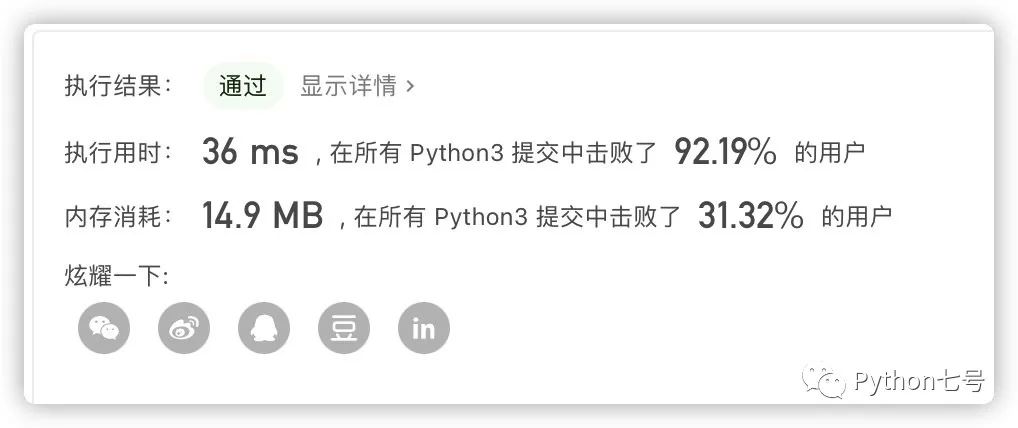
由于 leetcode 同时有很多人使用,因此不同的时间提交,服务器的计算压力是不同的,得出的结果会有少量的差异,这个理解就好。
到这里不知道你是否理解了回溯算法的思路。如果有不理解的地方,请在文末留言交流。
最后的话
其实不管多么复杂的算法,归根结底都逃离不开最基本的循环语句、if、else 的组合,再高级一点的,就是与栈、队列、递归的组合应用。
本文提到的回溯算法,本质就是暴力遍历多叉树(本题是 3 叉树)求解,先确定决策树,写出多叉树的遍历框架,然后填充内容。不要忘记在递归完成后撤销选择。如果还有点不理解,这里我提个问题:
请问二叉树前、中、后序遍历的区别是什么,你可能会说不就是访问根节点的顺序不同么,先访问根节点就是前序遍历....
其实这样的回答是错的,无论哪一种遍历,都是要先访问根节点的,不访问根节点,你怎么可能访问得到子节点?
真正的区别在于对根节点的处理是放在进入子节点的递归调用之前,还是在递归调用之后。前序遍历的代码在进⼊某⼀个节点之前的那个时间点执⾏,后序遍历代码在离开某个节点之后的那个时间点执⾏,如下图所示:
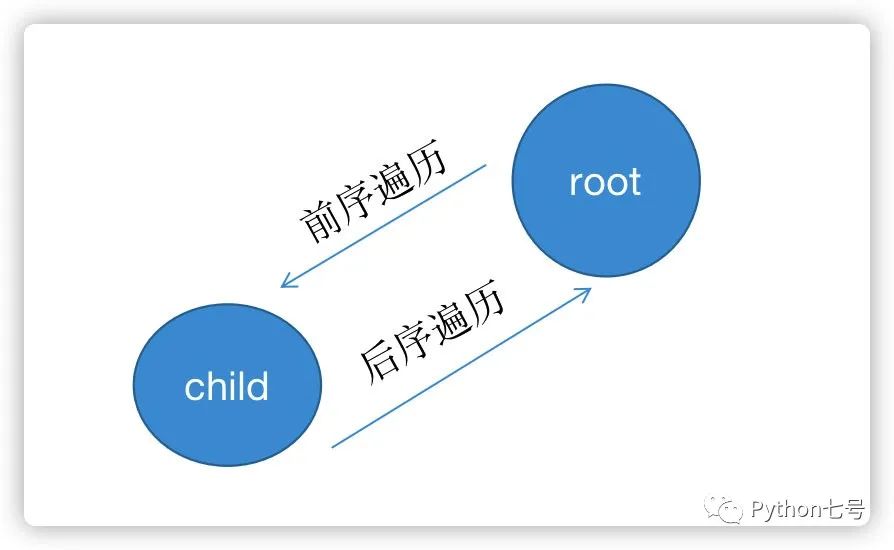
def trace(root):
##前序
trace(root.left)
##中序
trace(root.right)
##后序
因此后序遍历之后,需要撤销选择的 child,加入新的 child 进行遍历。
PS:如果你也在刷 Leetcode,我这里有一份从 Leetcode 中精选大概 200 左右的题目,去除了某些繁杂但是没有多少算法思想的题目,同时保留了面试中经常被问到的经典题目,对本号发消息回复「算法」即可获取,让你更高效地刷力扣。
如果觉得本文对你有用,请点赞在看转发支持,感谢老铁。
