小孩都看得懂的推荐系统,看不懂算我输 OK?

我还是推荐系统小白,因此对此课题理解相当浅显,但一定很好懂。这才是学一样新东西的正确开始方式。
01

故事的背景包括 4 个小孩和 5 部动画,每个小孩为每部动画打分
1 分代表最不喜欢
5 分代表最喜欢
02

悠悠觉得「小猪佩奇」还可以,给了 3 分。建立一个 4 × 5 的矩阵
每行代表一个小孩给所有动画打的分数
每列代表一部动画被所有小孩打的分数
当悠悠给「小猪佩奇」打完分后,在矩阵第 1 行第 1 列填入 3 分。
03

假设 4 个小孩为 5 部动画打分完毕,哪一个打分矩阵最像真的?
最左边不像,小孩的喜好不会这么千篇一律
最右边不像,小孩的喜好不会这么毫无联系
中间的最像,小孩的喜好会有一定的规律
04
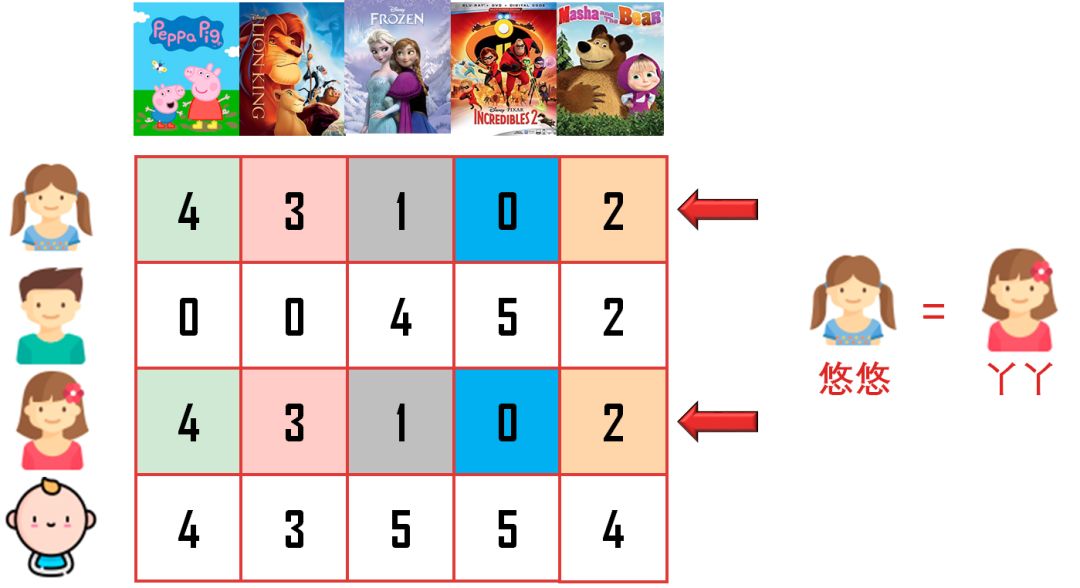
悠悠和丫丫年龄差不多,总在一起看动画片,她俩的对动画的品位出奇相似(5 部动画给出同样的评分),比如大爱「小猪佩奇」,小爱「狮子王」,不喜欢「冰雪奇缘」「超人特工队」「玛莎和熊」。
规律 1:不同用户的喜好可能相似。
05
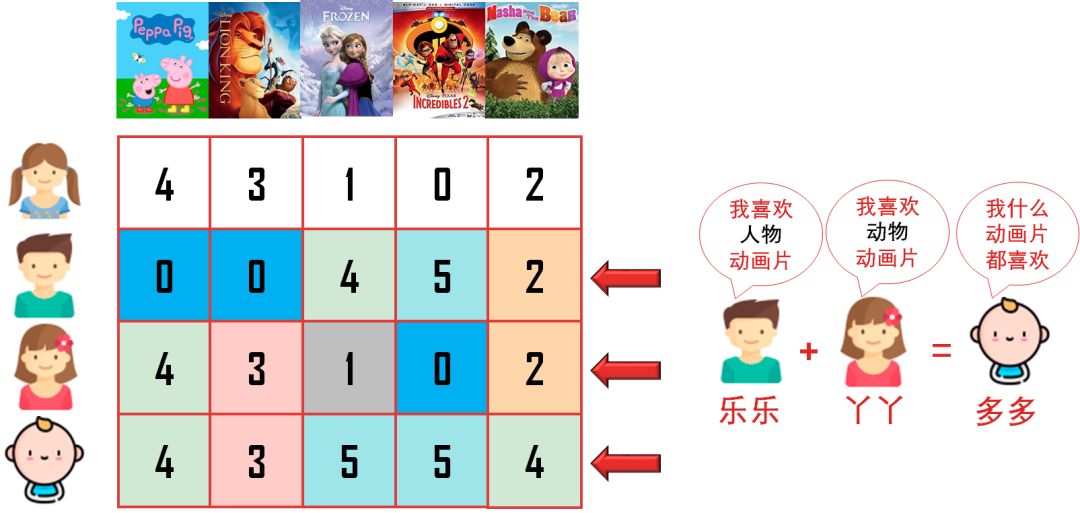
乐乐喜欢看带「人物」的动画,他给「冰雪奇缘」和「超人特工队」高分;丫丫喜欢看带「动物」的动画,她给「小猪佩奇」和「狮子王」高分;多多还比较小,只要是动画都喜欢,他给所有动画高分(多多给的分是乐乐和丫丫给的分之和)。
规律 2:一个用户的喜好可能包含其他多个用户的喜好。
06
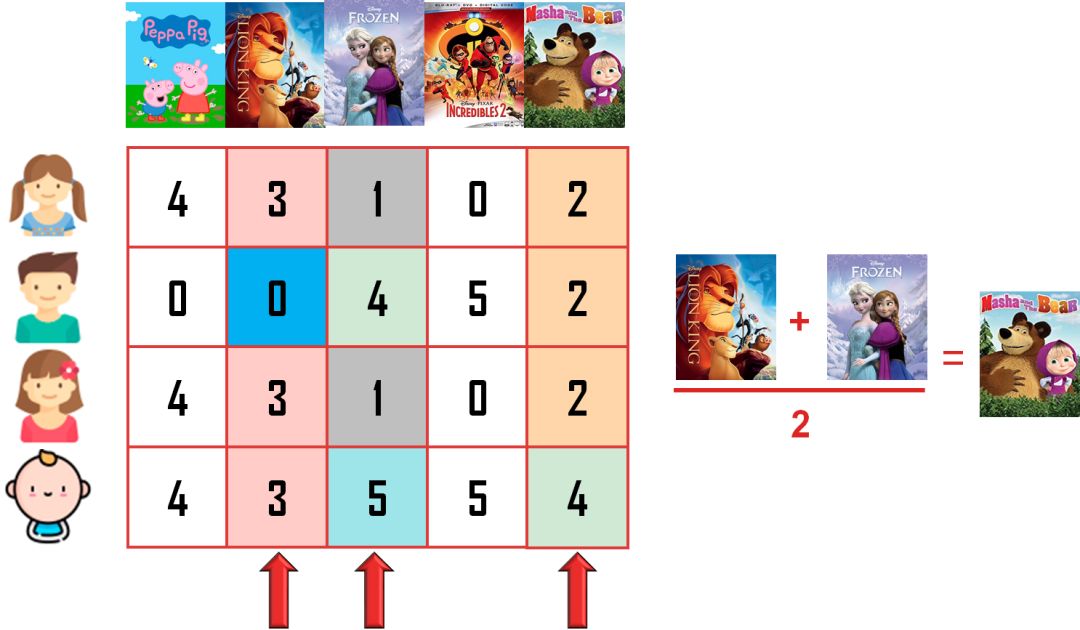
「玛莎和熊」的评分是「狮子王」和「冰雪奇缘」的评分的均值。可能原因是「狮子王」里只含有动物,「冰雪奇缘」里绝大部分是人,而「玛莎和熊」里既有动物又有人,而且数目相当。
规律 3:一个动画内容可能包含其他多个动画内容。
08

先看一个最简单的推荐系统。
当所有人给所有电影打 3 分,问丫丫应该给「超人特工队」打多少分?
从评分矩阵来看,每个人对每个电影喜欢一样,因此预测出丫丫会给「超人特工队」打 3 分。
09
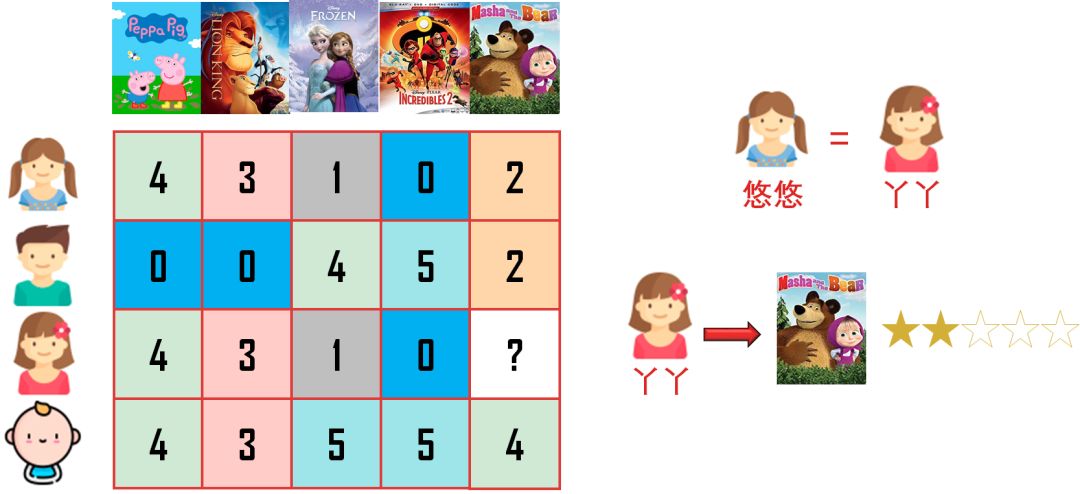
再看一个稍微复杂的推荐系统。
问丫丫应该给「玛莎和熊」打多少分?
从评分矩阵第一行和第三行来看,悠悠和丫丫的喜欢相同,因此预测出丫丫会给「玛莎和熊」打 2 分,和悠悠一样。
10
上面例子太简单,如果小孩有很多个,动画有很多部,我们怎么才能从评分矩阵中学到所有的规律呢?
答案:找到隐含特征!
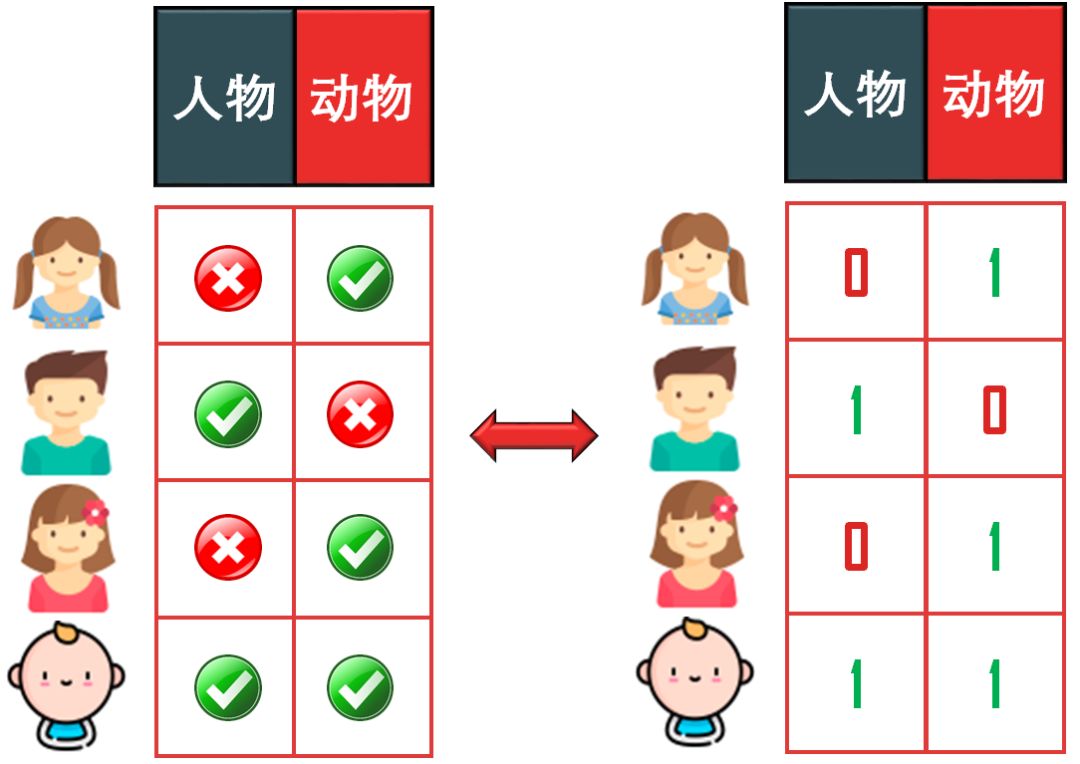
回到上面的例子,如果特征是动画片的类别,那么特征值有两个,人物类和动物类。那么根据不同小孩对这两类动画特征的喜好,如上图,
悠悠和丫丫喜欢动物类,不喜欢人物类
乐乐喜欢人物类,不喜欢动物类
多多都喜欢
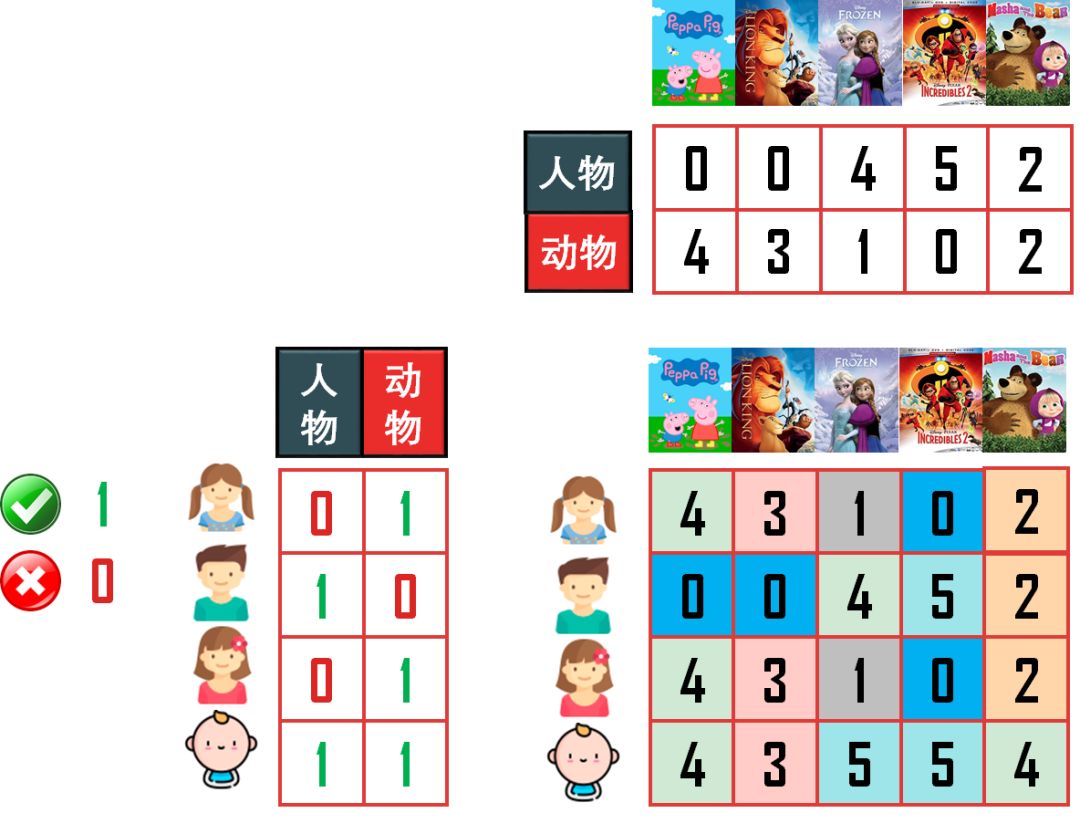
再根据具体动画片含这两类特征的比重,如下图

我们可以将 4 × 5 的评分矩阵分解成
4 × 2 的「小孩-特征」矩阵
2 × 5 的「特征-动画」矩阵
如下。
11
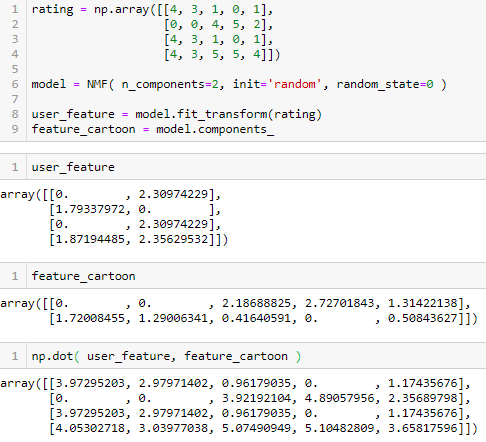
因此我们要做的事情就是讲评分矩阵分解成两个非负矩阵的乘积,专业术语是非负矩阵分解(Non-negative Matrix Factorization, NMF), 机器学习包 Scikit-Learn 里有实现哦。
import numpy as npfrom sklearn.decomposition import NMF
用上面数据试了下,虽然分别的矩阵不是完全一样,但矩阵中是 0 的还是 0,其他元素只是差了一个缩放因子(scaling factor),你看最后把两个分解矩阵相乘,差不到能得到原来的评分矩阵。
实际情况下,不可能每个小孩对每部动画都给出评分,因此不能直接用 NMF,那些缺失值才体会推荐系统的价值,我们要根据已有的评分来预测未给的评分,再决定是否推荐。
12

实际情况,打 ?都是未给出评分,这时
设「小孩-特征」矩阵为 U
设「特征-动画」矩阵为 V
用以下误差函数(只考虑未缺失的 Ri,j)
(Ri,j – U 第 i 行和 V 第 j 列内积)2
怎么解?梯度下降呗!解完 U 和 V 后相乘发现 R4,4 = 5,那么妥妥的给多多推荐狮子王!
让我知道你“在看”
