小孩都看得懂的 ROC
点击下面卡片关注“AI算法与图像处理”,选择加"星标"或“置顶”
重磅干货,第一时间送达
0
数据
一切要从分类问题开始,先看数据。
数据有两类,蓝点表示正类 (positive class),红点表示负类 (negative class)。

两个具体例子:
肿瘤诊断:恶性肿瘤 (正类)、良性肿瘤 (负类)
邮件分类:垃圾邮件 (正类)、正常邮件 (负类)
惯例:通常想预测出来的类别定义为正类。
1
模型
下图的线段当成模型,作用是将蓝点和红点分开。
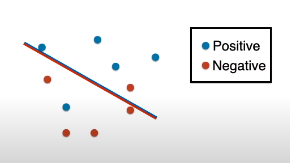
仔细看,这条线段被设计成红蓝相配,含义就是说面向线段红色部分的点被划分为红点,而面向线段蓝色部分的点被划分为蓝点。
2
模型会犯错误哦
从下图看有两个点分类错误,而它们是两种类型的错误。
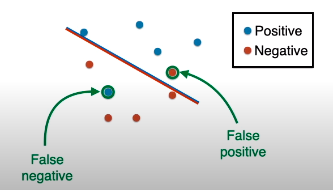
先看线段上面:红点 (真实负类) 被当作蓝点 (预测正类),该错误叫做假正类 (false positive)
再看线段下面:蓝点 (真实正类) 被当作红点 (预测负类),该错误叫做假负类 (false negative)
3
两个模型
让我们给相同的数据赋予两个故事。
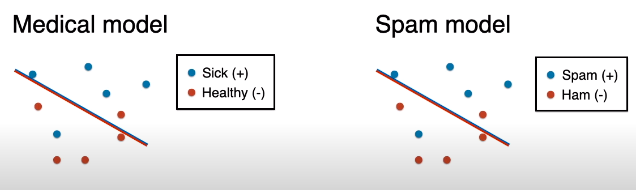
故事一讲述一个医用分类模型,它负责区分生病的人 (正类) 和健康的人 (负类)。
故事二讲述一个邮件分类模型,它负责区分垃圾邮件 (正类) 和正常邮件 (负类)。
让我们一一来研究它们。
5
医用分类模型
在此模型下,生病的人是正类,健康的人是负类,那么
把健康的人 (真实负类) 预测为生病的人 (预测正类),该错误叫做假正类 (false positive)。
把生病的人 (真实正类) 被当作健康的人 (预测负类),该错误叫做假负类 (false negative)
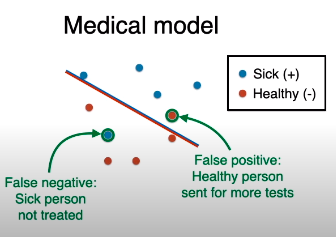
哪种错误更严重?
假负类是吧,人病了却预测没病不去治疗,万一是绝症后果不堪设想。
假正类还行,人没病却预测病了去测试,顶多花点时间花点钱嘛。
结论:医用分类模型应该减少假负类。
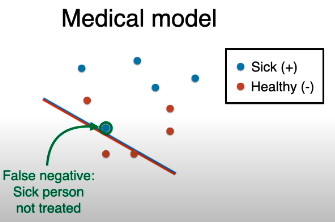
上图这个线段 (模型) 可还行,没有假负类,即便有增大假正类的代价。
6
邮件分类模型
在此模型下,垃圾邮件是正类,正常邮件是负类,那么
把正常邮件 (真实负类) 预测为垃圾邮件 (预测正类),该错误叫做假正类 (false positive)。
把垃圾邮件 (真实正类) 被当作正常邮件 (预测负类),该错误叫做假负类 (false negative)
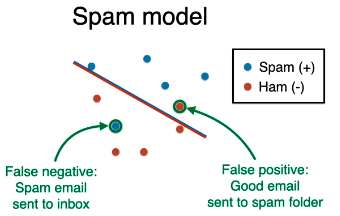
哪种错误更严重?
假正类是吧,正常邮件 (可能是很重要的邮件) 预测为垃圾邮件,放到垃圾站中,多耽误事儿啊。
假负类还行,垃圾邮件预测为正常邮件,呈现在你眼前,你删了不就完了么,多大点事儿啊。
结论:邮件分类模型应该减少假正类。

上图这个线段 (模型) 可还行,没有假正类,即便有增大假负类的代价。
7
记录错误
医用分类模型 (希望假负类最少) 和邮件分类模型 (希望假正类最少) 属于两个极端,绝大部分的分类模型在“中间”,即犯一点假负类,犯一点假正类。
那么如何记录假负类和假正类呢?
先从下图的最简单模型开始,请思考多个点分类错误?
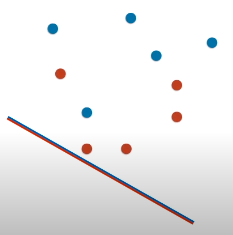
还记得线段被设计成红蓝相配的用意吗?面向线段蓝色部分的都被归类为蓝点,那么 5 个真实蓝点都预测对了,5 个真实红点都预测错了。
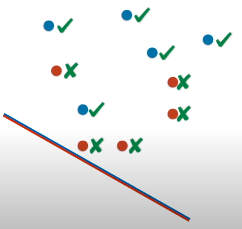
第 0 步:将上述结果用表格和网格图表示如下:

表格记录的正确红点个数为 0,正确蓝点个数为 5,在对应的网格图中,在坐标 (0, 5) 上面“放”一个点。
第 1 步:接着将线段延斜上方平移一下,现在正确红点个数变成 1,正确蓝点个数还是为 5,在对应的网格图中,在坐标 (1, 5) 上面“放”一个点。
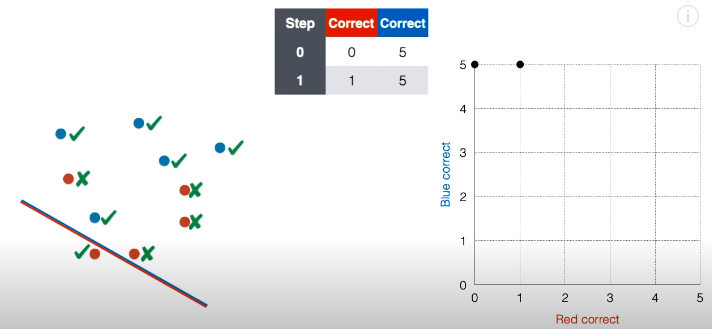
第 2 步:接着将线段延斜上方平移一下,现在正确红点个数变成 2,正确蓝点个数还是为 5,在对应的网格图中,在坐标 (2, 5) 上面“放”一个点。
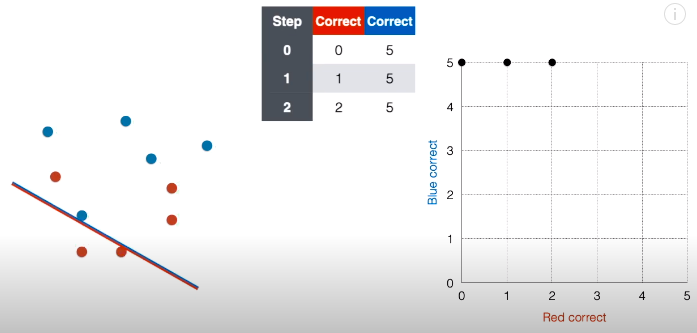
第 3 步:接着将线段延斜上方平移一下,现在正确红点个数还是为 2,正确蓝点个数变成 4,在对应的网格图中,在坐标 (2, 4) 上面“放”一个点。
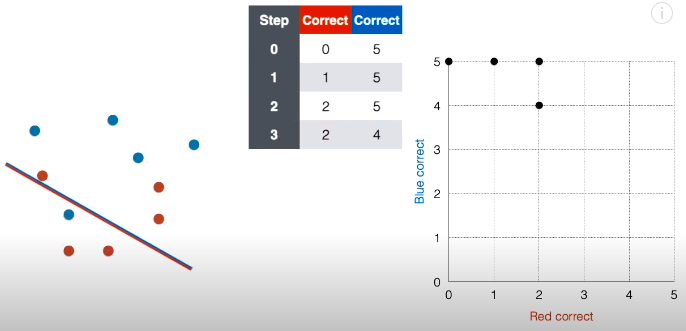
第 4 步:接着将线段延斜上方平移一下,现在正确红点个数变成 3,正确蓝点个数还是为 4,在对应的网格图中,在坐标 (3, 4) 上面“放”一个点。
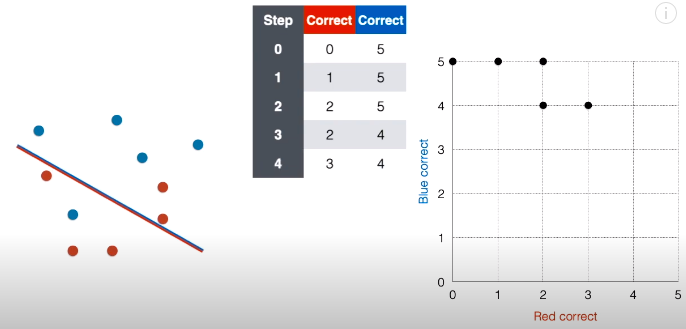
第 5 步:接着将线段延斜上方平移一下,现在正确红点个数变成 4,正确蓝点个数还是为 4,在对应的网格图中,在坐标 (4, 4) 上面“放”一个点。
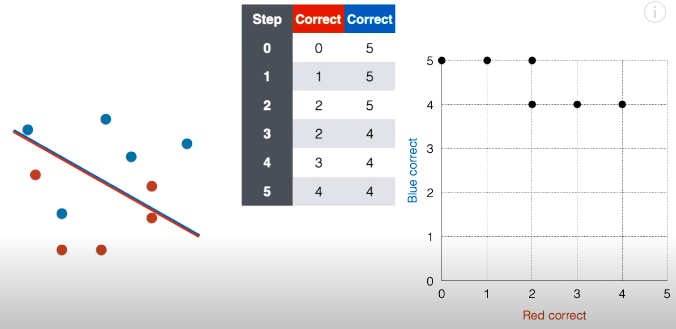
第 6 步:接着将线段延斜上方平移一下,现在正确红点个数还是为 4,正确蓝点个数变成 3,在对应的网格图中,在坐标 (4, 3) 上面“放”一个点。
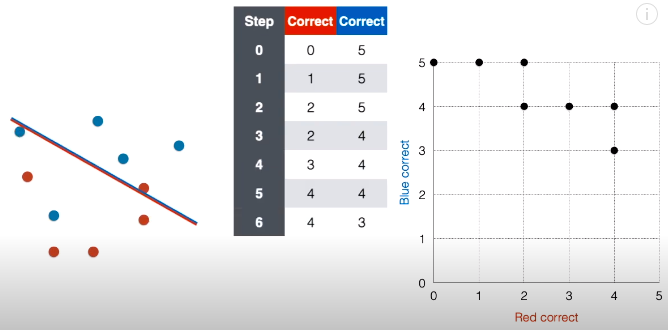
第 7 步:接着将线段延斜上方平移一下,现在正确红点个数变成 5,正确蓝点个数还是为 3,在对应的网格图中,在坐标 (5, 3) 上面“放”一个点。
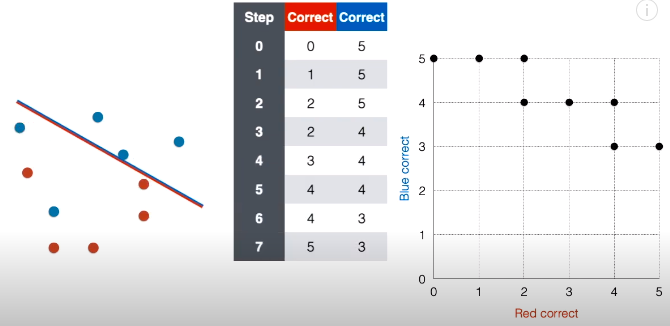
第 8 步:接着将线段延斜上方平移一下,现在正确红点个数还是为 5,正确蓝点个数变成 2,在对应的网格图中,在坐标 (5, 2) 上面“放”一个点。
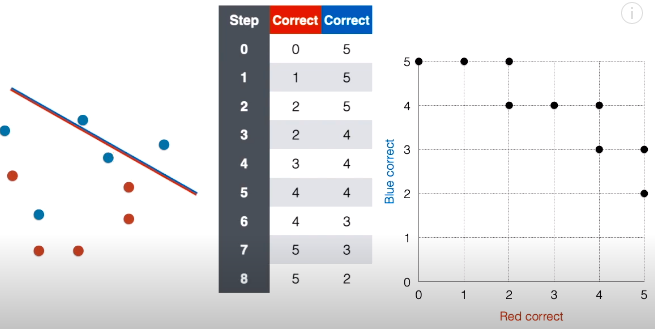
第 9 步:接着将线段延斜上方平移一下,现在正确红点个数还是为 5,正确蓝点个数变成 1,在对应的网格图中,在坐标 (5, 1) 上面“放”一个点。
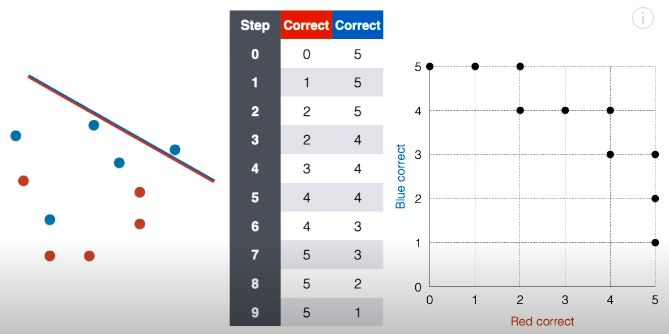
第 10 步:接着将线段延斜上方平移一下,现在正确红点个数还是为 5,正确蓝点个数变成 0,在对应的网格图中,在坐标 (5, 0) 上面“放”一个点。
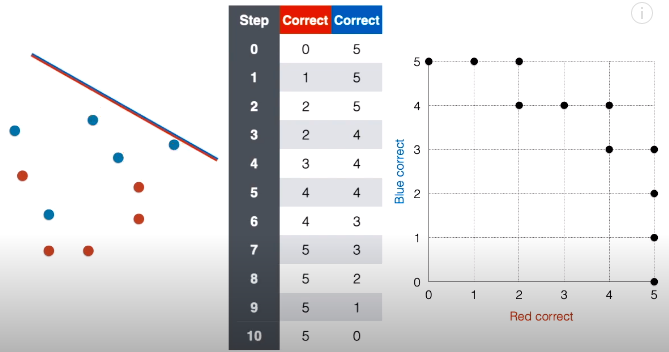
流程结束,前戏做完,下面介绍 ROC 和 AUC。
8
ROC 和 AUC
ROC 全称是 receiver operating characteristic,ROC 曲线中文叫做接收者操作特征曲线。为什么叫这个名字其实我也不知道,也不想知道,又绕口又恶心。
我们只需要知道网格图那些点连成的线就是 ROC 曲线。
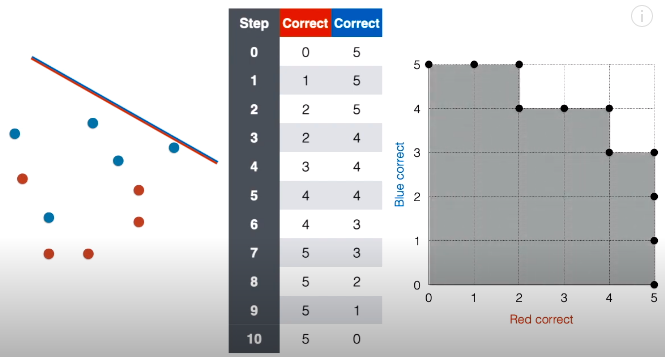
ROC 曲线以下和横轴竖轴包围起来的面积叫做 AUC,全称是 Area Under the Curve,这倒是怪形象的。阴影包含 21 个小正方形,不难看出其面积为 21。
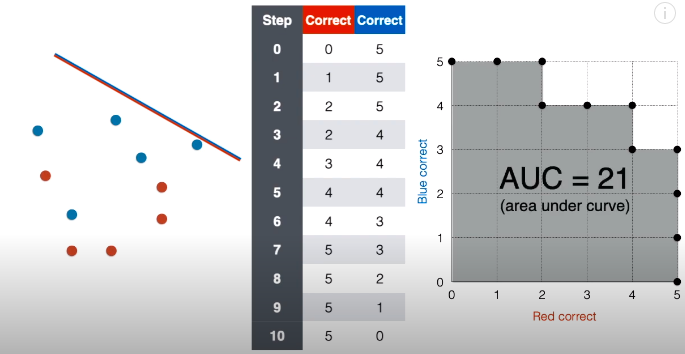
通常为了比较不同模型好坏,AUC 会做一个标准化,即用阴影面积除以整个网格面积,则得到 21/25 = 0.84。
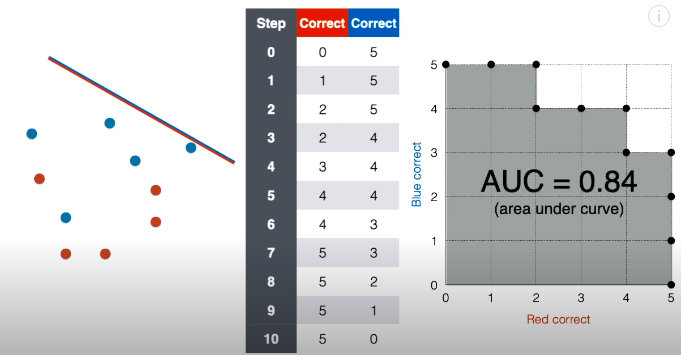
一般来说,AUC 越高,模型越好。
9
模型背景
在绝大多数背景下选择分类模型,下图框出的点 (4, 4) 的对应模型“最优”,只有一个假负类和假正类的错误。
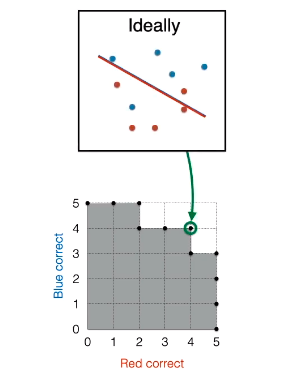
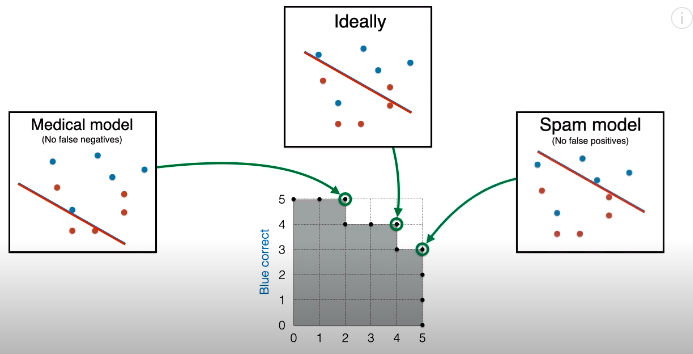
如果赋予医用背景,那么 (2, 5) 点对应的模型最优,没有假负类,假正类在同等条件下最少。
如果赋予邮件背景,那么 (5, 3) 点对应的模型最优,没有假正类,假负类在同等条件下最少。
10
模型选择
为了解释本节内容,注意数据稍微有些改变。
仔细观看红点蓝点的位置,然后想想将线段往斜上方平移,总是有大概一半情况分类错误。
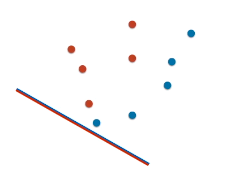
用上述方法绘制 ROC 曲线并计算 AUC 得到 0.52。
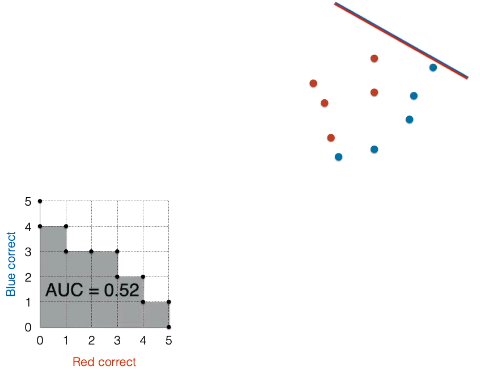
结论:随机模型的 AUC 在 0.5 左右。
模型二比随机模型稍微好些。
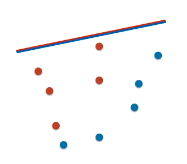
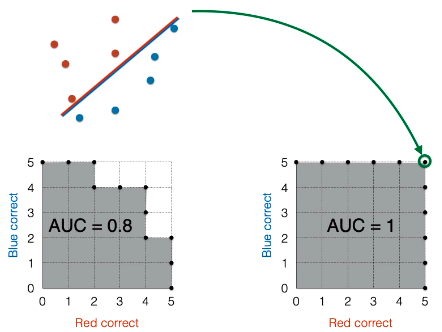
将线段往斜下方平移,用上述方法绘制 ROC 曲线并计算 AUC 得到 0.8。
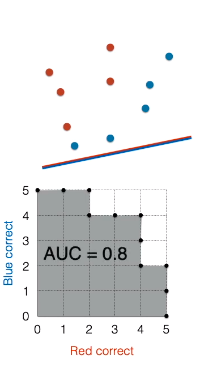
模型三是完美模型。
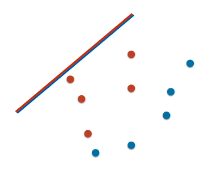
将线段往斜下方平移,用上述方法绘制 ROC 曲线并计算 AUC 得到 1,下图点 (5, 5) 对应的模型是完美的,没有任何分类错误。
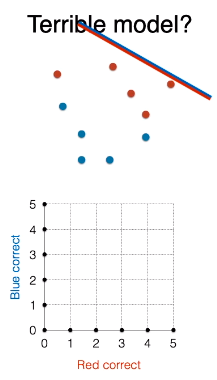
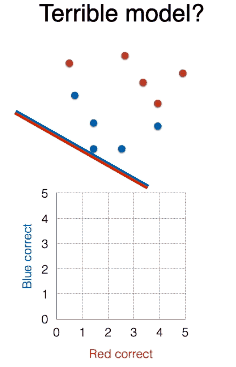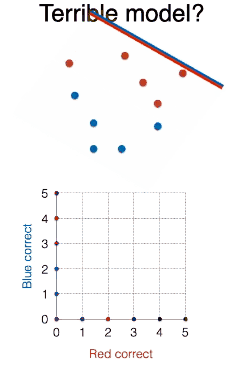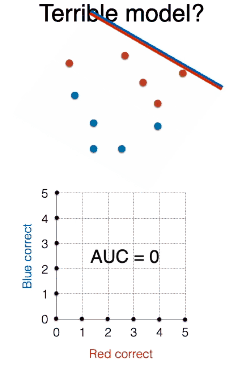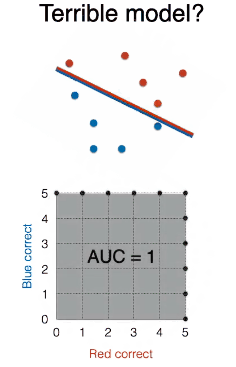
下图的模型是超烂模型么?
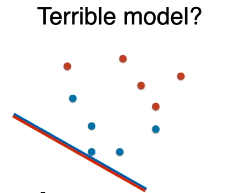
将线段往斜上方平移,用上述方法绘制 ROC 曲线并计算 AUC 得到 0。
比较上述四个模型的 AUC。

超烂模型真的比随机模型烂吗?其实不然,其实将烂模型,哦不对,烂线段,转个 180 度,是不是变成完美模型了?AUC 是不是为 1 了?
就好比一个天天预测股价涨跌的人,正确率为 0,你根据他的预测反向操作,你就是股神。
所以最烂模型是随机模型!
个人微信(如果没有备注不拉群!) 请注明:地区+学校/企业+研究方向+昵称
下载1:何恺明顶会分享
在「AI算法与图像处理」公众号后台回复:何恺明,即可下载。总共有6份PDF,涉及 ResNet、Mask RCNN等经典工作的总结分析
下载2:终身受益的编程指南:Google编程风格指南
在「AI算法与图像处理」公众号后台回复:c++,即可下载。历经十年考验,最权威的编程规范!
下载3 CVPR2021 在「AI算法与图像处理」公众号后台回复:CVPR,即可下载1467篇CVPR 2020论文 和 CVPR 2021 最新论文
点亮  ,告诉大家你也在看
,告诉大家你也在看
