数分面试题!20m³的空间可以装多少乒乓球?
“20m³的空间可以装多少乒乓球?”

好的,有人可能已经算出结果了。
已知:
乒乓球的标准直径是4cm,也就是0.04m;
球形体积公式为
然后用总空间体积除以单个乒乓球体积就行。
等一下,也许应该先问几个问题:
Q1: 20m³的空间是怎样的?
如果是0.02m*20m*50m的容器,看起来就像一个很扁的盒子(乒乓球塞进去就瘪了)或者超大的盘子,对吧,不过这里对空间的要求是封闭的,也就是乒乓球不能超越容器的边界(不能在盘子里“堆尖尖”);
Q2: 乒乓球是要保证完好地装进去?
是的,把乒乓球搞成渣渣这种操作是不允许的,就是普通的一个一个的乒乓球,不能破坏乒乓球。
不过我改动了下,先设定体积(模糊信息),如果直接开算,那上面的两个问题就是潜在的坑。
在问题的信息不全或者模糊的时候,首先就是要“澄清问题”,看看问题的定义、边界或限定是怎样的。
好的,我们继续,现在是2*2*5的20m³的封闭空间,能装多少个完整的乒乓球?
接下来开始计算,前面已知了乒乓球的大小和球形体积公式,那么有
需要注意的是:
单位要对齐,半径是2厘米要换算到米;
速算的时候尽量取整,比如 可以直接约等于4
不过,这样对么?

下面是当时的“简单思路”:
把每个乒乓球看成是立方体,长宽高各是4厘米,那计算这个2*2*5的空间能装多少个这样的小立方体就行了。,取整就是30W。
为什么这样想?
这个思路最简单,最容易算;
肯定不能直接用乒乓球体积来当分母的,因为乒乓球之间有空隙(所以除非房间里有黑洞,怎么可能装下?);
在这个思路下,乒乓球的排列方式是行列整齐的,从侧面或者俯视角度都是方方正正的。

不过,优化乒乓球的排列方式,还可以放更多。
首先,从底向上一层一层地摆放时,可以调整每一层小球的位置使得更紧密。
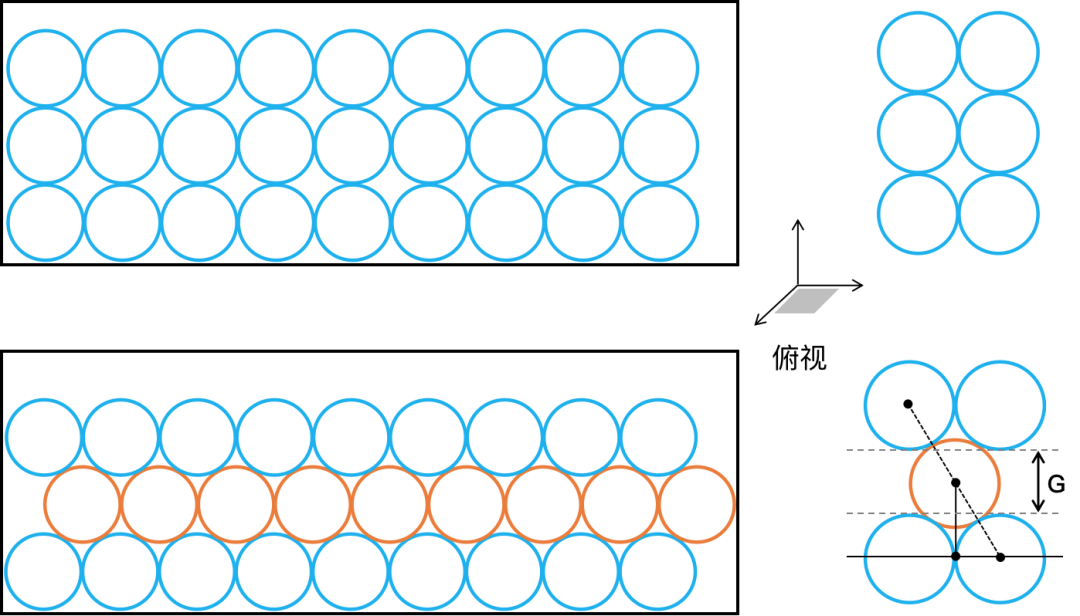
设乒乓球的半径为 ,“凹进去”的“夹层”(橙色小球)的高度 .
可以由
得到 ,“夹层”高度 是小于球的直径,所以能更有效利用空间。
不考虑最后一层的“边界情形”或者“夹层”的小球数相对于“普通层”有±1的误差,就按一排“蓝色”一排“橙色”这样排列,那么相对于整整齐齐排列,可以容纳的小球数量是之前的 倍
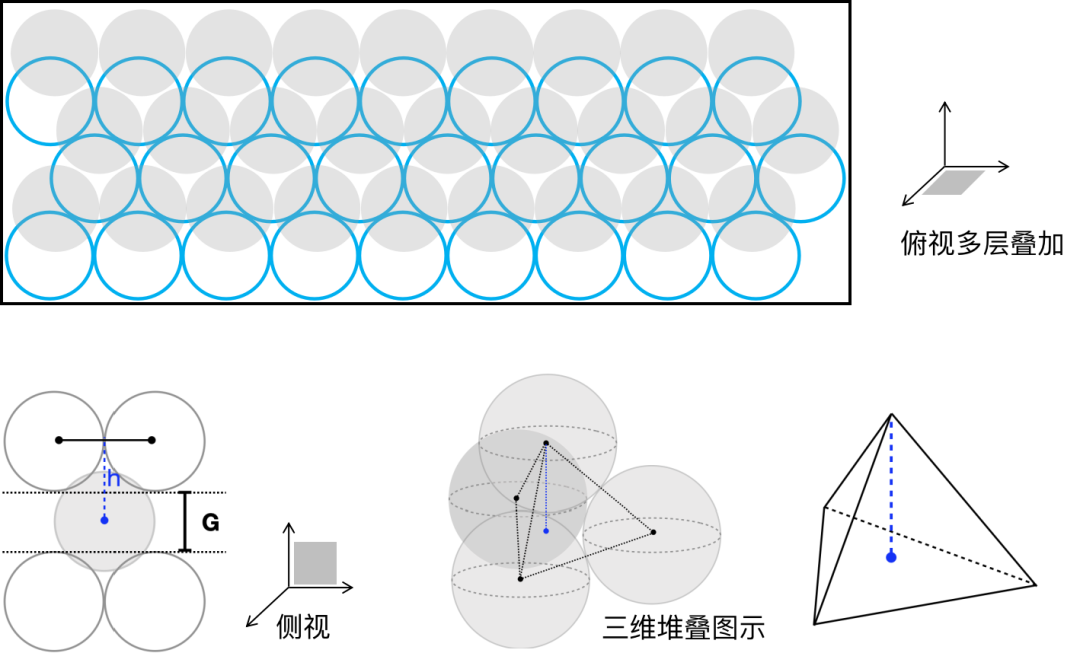
其中:
互切的4个小球的球心组成正四面体,棱边长度是2R
可以算得 .
进而得到
这样堆叠的效率就是整齐摆放的 倍
同时运用上面两种摆放策略,那么理论上可以装的乒乓球数量就是
这就是优化后的排列方案。
