PyTorch学习系列教程:Tensor如何实现自动求导
导读
今天本文继续PyTorch学习系列。虽然前几篇推文阅读效果不是很好(大体可能与本系列推文是新开的一个方向有关),但自己选择的路也要坚持走下去啊!
前篇推文介绍了搭建一个深度学习模型的基本流程,通过若干个Epoch即完成了一个简单的手写数字分类模型,效果还不错。在这一过程中,一个重要的细节便是模型如何学习到最优参数,答案是通过梯度下降法。实际上,梯度下降法是一类优化方法,是深度学习中广泛应用甚至可称得上是深度学习的基石。本篇不打算讲解梯度下降法,而主要来谈一谈Tensor如何实现自动求导,明白这一过程方能进一步理解各种梯度下降法的原理。
Tensor中的自动求导:与梯度相关的属性,前向传播和反向传播
自动求导探索实践:以线性回归为例,探索自动求导过程
Tensor是PyTorch中的基础数据结构,构成了深度学习的基石,其本质上是一个高维数组。在前序推文中,实际上提到过在创建一个Tensor时可以指定其是否需要梯度。那么是否指定需要梯度(requires_grad)有什么区别呢?实际上,这个参数设置True/False将直接决定该Tensor是否支持自动求导并参与后续的梯度更新。具体来说,Tensor数据结构中,与梯度直接相关的几个重要属性间的关系如下:
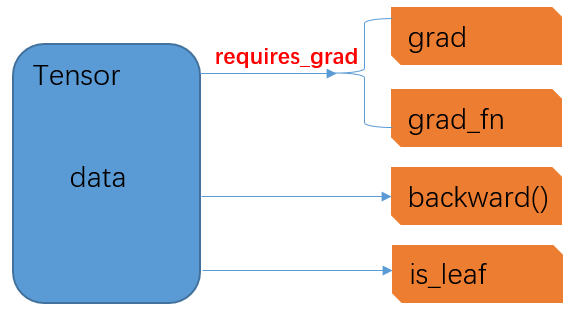
原创拙图,权当意会
在一个Tensor数据结构中,最核心的属性是data,这里面存储了Tensor所代表的高维数组(当然,这里虽然称之为高维,但实际上可以是从0维开始的任意维度);
通过requires_grad参数控制两个属性,grad和grad_fn,其中前者代表当前Tensor的梯度,后者代表经过当前Tensor所需求导的梯度函数;当requires_grad=False时,grad和grad_fn都为None,且不会存在任何取值,而只有当requires_grad=True时,此时grad和grad_fn初始取值仍为None,但在后续反向传播中可以予以赋值更新
backward(),是一个函数,仅适用于标量Tensor,即维度为0的Tensor
is_leaf:标记了当前Tensor在所构建的计算图中的位置,其中计算图既可看做是一个有向无环图(DAG),也可视作是一个树结构。当Tensor是初始节点时,即为叶子节点,is_leaf=True,否则为False。
目前,Tensor支持自动求导功能对数据类型的要求是仅限于浮点型:" As of now, we only support autograd for floating point Tensortypes ( half, float, double and bfloat16) and complexTensortypes (cfloat, cdouble). "——引自PyTorch官方文档
前向传播,就是依据计算流程实现数据(data)的计算和计算图的构建:
反向传播,反向传播就是依据所构建计算图的反方向递归求导和赋值梯度:
而如果用图形化描述这一过程,则是:
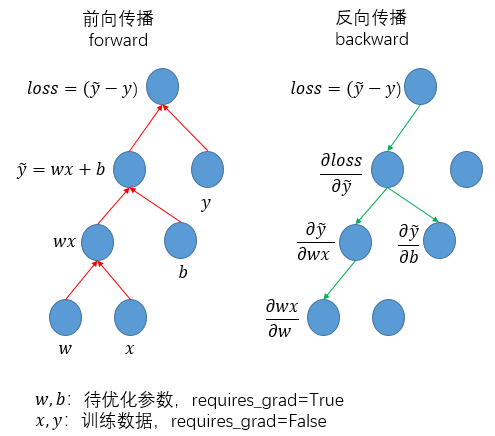
其中,在前向传播过程中,是按照流程完成从初始输入(一般是训练数据+网络权重)直至最终输出(一般是损失函数)的计算过程,同步完成计算图的构建;而在反向传播过程中,则是通过调用loss.backward()函数,依据计算图的相反方向递归完成各级求导(本质上就是求导的链式法则)。同时,对于requires_grad=False的tensor,在反向传播过程中实际不予以求导和更新,相应的反向链条被切断。
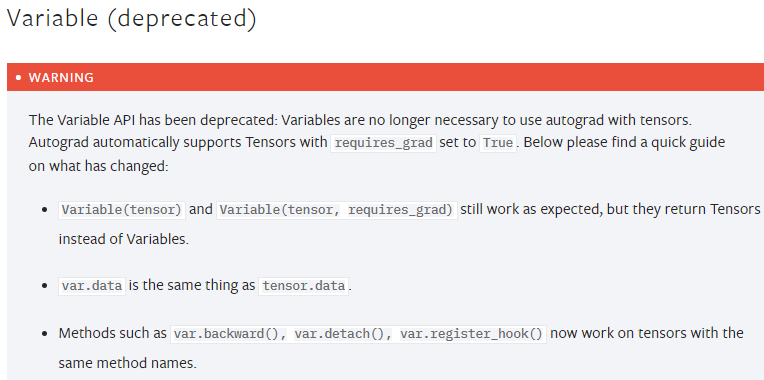
已进入历史舞台的Variable类型
这里,我们以一个简单的单变量线性回归为例演示Tensor的自动求导过程。
1.创建训练数据x, y和初始权重w, b
# 训练数据,目标拟合线性回归 y = 2*x + 3x = torch.tensor([1., 2.])y = torch.tensor([5., 7.])# 初始权重,w=1.0, b=0.0w = torch.tensor(1.0, requires_grad=True)b = torch.tensor(0.0, requires_grad=True)
此时查看w, b和x, y的梯度相关的各项属性,结果如下
# 1. 注意:x和y设置为requires_grad=Falsex.grad, x.grad_fn, x.is_leaf, y.grad, y.grad_fn, y.is_leaf# 输出:(None, None, True, None, None, True)# 2. w和b初始梯度均为None,且二者均为叶子节点w.grad, w.grad_fn, w.is_leaf, b.grad, b.grad_fn, b.is_leaf# 输出:(None, None, True, None, None, True)
2.构建计算流程,实现前向传播
# 按计算流程逐步操作,实现前向传播wx = w*xwx_b = wx + bloss = (wx_b - y)loss2 = loss**2loss2_sum = sum(loss2)
查看各中间变量的梯度相关属性:
# 1.查看是否叶子节点wx.is_leaf, wx_b.is_leaf, loss.is_leaf, loss2.is_leaf, loss2_sum.is_leaf# 输出:(False, False, False, False, False)# 2.查看gradwx.grad, wx_b.grad, loss.grad, loss2.grad, loss2_sum.grad# 触发Warning# UserWarning: The .grad attribute of a Tensor that is not a leaf Tensor is being accessed. Its .grad attribute won't be populated during autograd.backward(). If you indeed want the .grad field to be populated for a non-leaf Tensor, use .retain_grad() on the non-leaf Tensor. If you access the non-leaf Tensor by mistake, make sure you access the leaf Tensor instead. See github.com/pytorch/pytorch/pull/30531 for more informations. (Triggered internally at aten\src\ATen/core/TensorBody.h:417.)return self._grad# 输出:(None, None, None, None, None)3.查看grad_fnwx.grad_fn, wx_b.grad_fn, loss.grad_fn, loss2.grad_fn, loss2_sum.grad_fn# 输出:(0x23a875ee550 >,0x23a875ee8e0 >,0x23a875ee4c0 >,0x23a875ee490 >,0x23a93dde040 >)
3.对最终的loss调用backward,实现反向传播
loss2_sum.backward()依次查看各中间变量和初始输入的梯度
# 1. 中间变量(非叶子节点)的梯度仅用于反向传播,但不对外暴露wx.grad, wx_b.grad, loss.grad, loss2.grad, loss2_sum.grad# 输出:(None, None, None, None, None)# 2. 检查叶子节点是否获得梯度:w, b均获得梯度,x, y不支持求导,仍为Nonew.grad, b.grad, x.grad, y.grad# 输出:(tensor(-28.), tensor(-18.), None, None)
至此,即通过前向传播的计算图和反向传播的梯度传递,完成了初始权重参数的梯度赋值过程。注意,这里w和b是网络待优化参数,而一旦二者有了梯度,则可进一步应用梯度下降法予以更新。
而后,带入两组训练数据(x, y)=(1, 5)和(x, y)=(2, 7),并将两组训练数据对应的梯度求和:
# w的梯度:2*(1*1 + 0 - 5)*1 + 2*(1*2 + 0 - 7)*2 = -28# b的梯度:2*(1*1 + 0 - 5) + 2*(1*2 + 0 - 7) = -18
显然,手动计算结果与上述演示结果是一致的。
注意:在多个训练数据(batch_size)参与一次反向传播时,返回的参数梯度是在各训练数据上的求得的梯度之和。
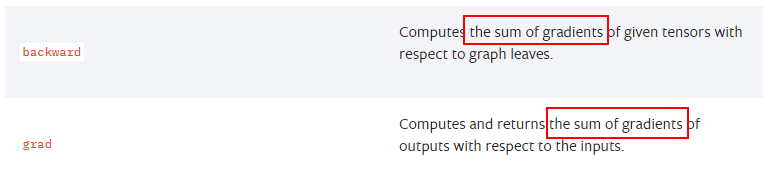
摘自PyTorch官网
相关阅读:
