机器学习之——自动求导
共 2347字，需浏览 5分钟
·
2021-10-13 19:05
点击上方“小白学视觉”，选择加"星标"或“置顶”
重磅干货，第一时间送达
本文转自|机器学习算法工程师
随机梯度下降法（SGD）是训练深度学习模型最常用的优化方法。在前期文章中我们讲了梯度是如何计算的，主要采用BP算法，或者说利用链式法则。但是深度学习模型是复杂多样的，你不大可能每次都要自己使用链式法则去计算梯度，然后采用硬编程的方式实现。
而目前的深度学习框架其都是实现了自动求梯度的功能，你只关注模型架构的设计，而不必关注模型背后的梯度是如何计算的。不过，我们还是想说一说自动求导是如何实现的。
这里我们会讲几种常见的方法，包括数值微分(Numerical
Differentiation)，符号微分(Symbolic Differentiation)，前向模式（Forward Mode)和反向模式(Reverse Mode)。
数值微分方式应该是最直接而且简单的一种自动求导方式。从导数的定义中，我们可以直观看到：
当h接近0时，导数是可以近似计算出来的。可以看到上面的计算式几乎适用所有情况，除非该点不可导。可是数值微分却有两个问题，第一个就是求出的导数可能不准确，这毕竟是近似表示，比如要求f(x)=x^2在零点附近的导数，如果h选取不当，你可能会得到符号相反的结果，此时误差就比较大了。第二个问题是对于参数比较多时，对深度学习模型来说，上面的计算是不够高效的，因为每计算一个参数的导数，你都需要重新计算f(x+h)。但是数值运算有一个特殊的用武之地就是在于可以做梯度检查（Gradient check），你可以用这种不高效但简单的方法去检查其他方法得到的梯度是否正确。
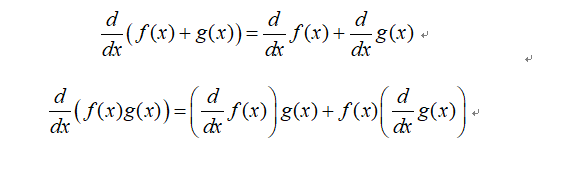
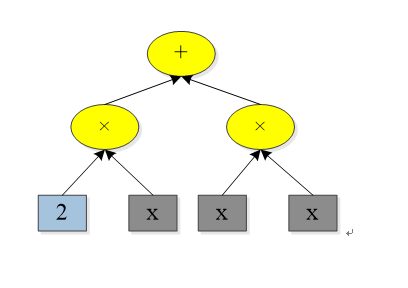
当我们将符号表达式用表达式树表示时，可以利用加法规则和乘法规则进行自动求导。比如我们要求符号表达式f(x)=2x+x^2，可以展开成如下图的表达式树：
利用求导规则，可以求出：
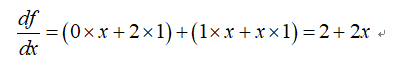
基于表达式树和求导规则，我们可以得到最终的导数。有一点要注意的是，符号微分不一定会得到简化的导数，因为计算机可能并不能进行智能的简化。所以，如果表达式树结构较复杂时，得到的导数表达式会相当复杂，也许出现表达式爆炸现象。
前向模式最简单明了，其基于的是二元数（dual numbers）。我们先来讲解一下二元数，其基本格式如下所示：
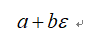
其中a和b都是实数，而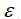
是无穷小量，你可以认为其无限接近0，但是并不等于0，并且
，这是借鉴了微积分中的概念。所以，你可以认为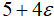
是一个接近5的数。对于二元数，其满足简单的加法和乘法规则：
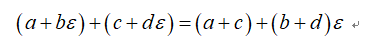
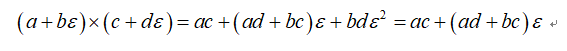
对于二元数，其更重要的一个特性是：
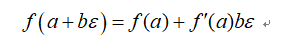
这意味着，我们只需要计算出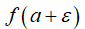
，就可以得到
以及其对应的导数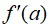
。所以，一个前向计算过程可以同时得到函数值与其导数，这就是前向模式的原理。举例来说，如果要计算f(x)=2x+x^2在x=2处的函数值与导数，其计算过程如下所示：
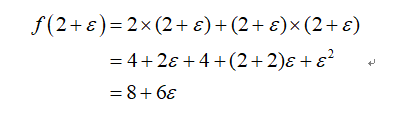
参考资料
1. Automatic Differentiation in Machine Learning: a Survey,
https://arxiv.org/pdf/1502.05767.pdf
2. Hands-On Machine Learning with Scikit-Learn and TensorFlow, Aurélien Géron, 2017.
好消息，小白学视觉团队的知识星球开通啦，为了感谢大家的支持与厚爱，团队决定将价值149元的知识星球现时免费加入。各位小伙伴们要抓住机会哦！
交流群
欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~