需求可拆分及带时间窗的车辆路径规划问题(SDVRPTW)简介

前言
今天为大家介绍需求可拆分的带时间窗车辆路径问题(Split Delivery Vehicle Routing Problem with Time Window,简称SDVRPTW )。而求解技术是精确算法之王中王——分支定价割平面法(Branch-Price-Cut,简称BPC),因为国内少有这类型算法的介绍,今天小编就给大家分享一下咯。
俗话说得好,一口吃不成胖子。因为BPC的框架是分支定界(Branch-and-bound),核心是列生成(Column Generation),可能涉及的技术是Labeling Algorithm。如果大家对上述部分的知识有所遗忘,可以先温习以下推文再进行阅读。

背景介绍和问题性质
模型建立
BPC技术简介
相关研究及问题变式
参考文献
1
背景介绍和问题性质
传统的VRPTW一般假设每个客户的需求量小于车辆的最大载重,所以一辆车可以一次性满足客户的需求。VRPTW的介绍见下面推文:
干货|十分钟快速掌握CPLEX求解VRPTW数学模型(附JAVA代码及CPLEX安装流程)
在实际生活中,客户需求也可能会大于车辆的最大载重,在要求一辆车至多访问客户一次的条件下,就需要多辆车服务同一个客户,于是诞生了SDVRPTW。
当然,如果客户需量求小于车的容量,因为客户的需求可拆分(split,即一次送货量小于客户需求),物流公司也可能获得经济上的收益。举个例子。
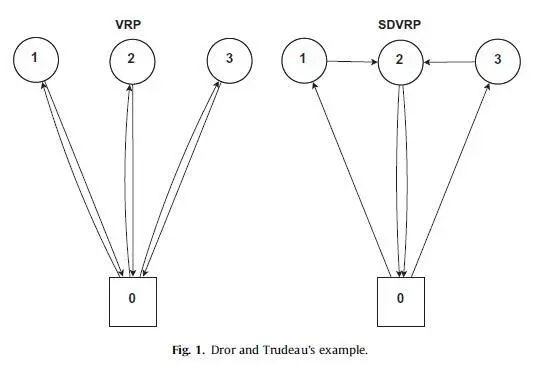
假设客户1、2、3的需求分别为3,4,3;每个客户离depot 0的距离都是20,客户之间的距离都是2;每辆车的最大载重为5;则VRP的最优解(左图)为3辆车,总距离为120;SDVRP的最优解(右图)为2辆车,总距离为84。
虽然SDVRPTW是VRPTW对约束的松弛,但是前者模型的建立和算法的设计却更加复杂。因为一旦客户允许被访问多次,那我们很难在顶点用唯一的变量分别表示该客户每次接受服务的配送量和服务时间,这无疑为模型定义和算法带来极大的挑战。
所以有必要剖析SDVRPTW的性质,为复杂的问题求解提供帮助。对于任意行驶成本和行驶时间均满足三角不等式关系的SDVRPTW实例,存在一个最优解具备以下几个性质:
性质1:对解中任意两条路线,它们共同访问的客户数目不超过1个。
性质2:每一条连接两个客户点的边最多被正向或反向经过一次。
性质3:每条路线中的客户都至多被访问一次。
例如当0表示depot,送货给拆分需求的客户1和2时,则允许存在两条0-1-0的路线,但不允许0-1-2-0和0-2-1-0同时存在,因为此时违反了性质1和性质2。

2
模型建立
模型建立引用Desaulniers(2010)提出的arc-flow模型,符号定义决定直接使用原文展示,不然总觉得词不达意。
因为模型在求解的时候会先进行松弛,为了使模型下界更好,通常会引进有效不等式,所以需要以下符号定义,假设U是客户集合N的一个子集。

额外的符号说明如下:


综上建立如下arc flow模型:
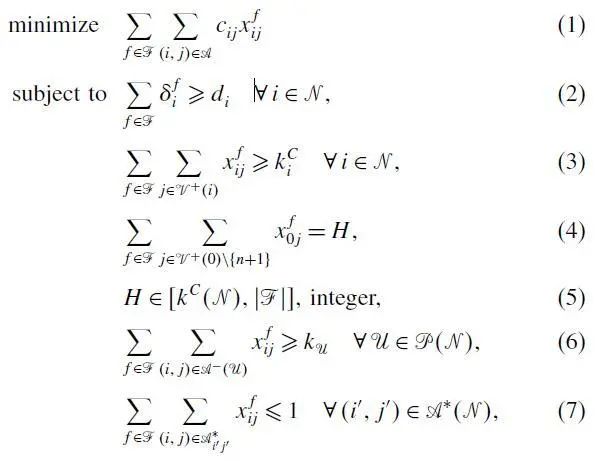
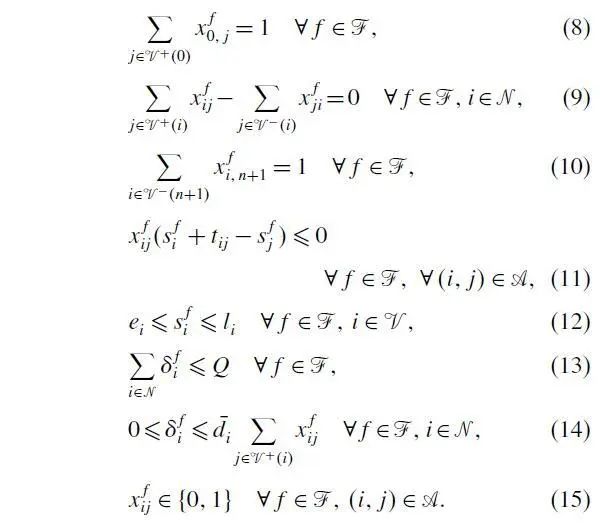
目标函数(1)表示最小化车辆行驶成本;
约束(2)确保每个客户的需求得到满足;
约束(3)-(6)虽然是多余的约束,但是可以加强模型松弛的效果,其中(3)表示访问客户需要的最小车辆数;(4)表示共调度的车辆数;(5)表示共调度的车辆数的上下界;(6)表示k-path不等式;
约束(7)由性质2每条边至多经过一次得到,关于arc的有效不等式,也是为了加强模型松弛效果;
约束(8)-(10)定义了路径的结构,从depot 0出发,最后回到depot n+1;
约束(11)-(12)确保不违反每个客户的时间窗;
约束(13)确保不违反车辆的最大载重约束;
约束(14)表示如果车辆访问了客户,则有相应的配送量,且不得超过该客户的总需求;
约束(15)为决策变量的取值约束。

3
BPC技术简介
首先我们对上文提到的arc-flow模型进行转换。因为arc-flow模型虽然可以非常恰当地描述SDVRPTW模型,但是松弛后的下界比较差,不利于算法的收敛,而将模型转化为set partitioning模型后再松弛,可以得到更好的下界。转化后的模型称为master problem(MP),需要下列的符号定义:


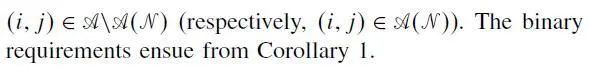
注:Corollary 1为前文提到的性质2
综上建立如下set partitioning模型(MP):

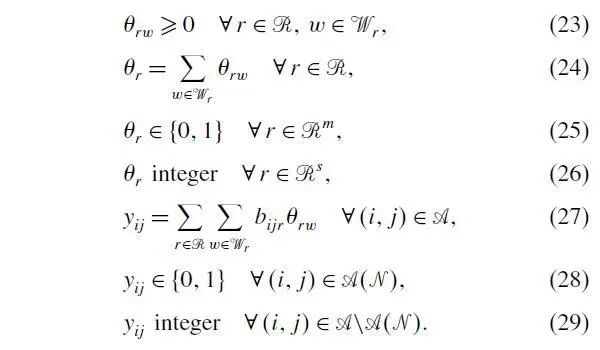
目标函数(16)表示最小化车辆行驶成本;
约束(17)-(22)等价于约束(2)-(7);
约束(23)确保MP的决策变量θ_rw非负;
约束(24)和(27)分别表示路径θ_r和弧y_ij与决策变量的关系;
剩余约束为变量的取值约束。
但MP的不足在于包含大量的变量(路径),为了解决这个问题,可以利用分支定价割平面算法(BPC)进行处理,下面介绍的技术框架也是由Desaulniers(2010)提出的。BPC是分支定界法的一种延伸,其外部调用分支定界法的框架,在分支定界树(Branch)的每个结点上通过列生成(Price)求解set partitioning模型的线性松弛来得到该节点的下界,并通过引入有效不等式(Cut)改善下界。下图引用自舒胜男的硕士论文(见文献6),流程图详细解释了算法的框架细节。
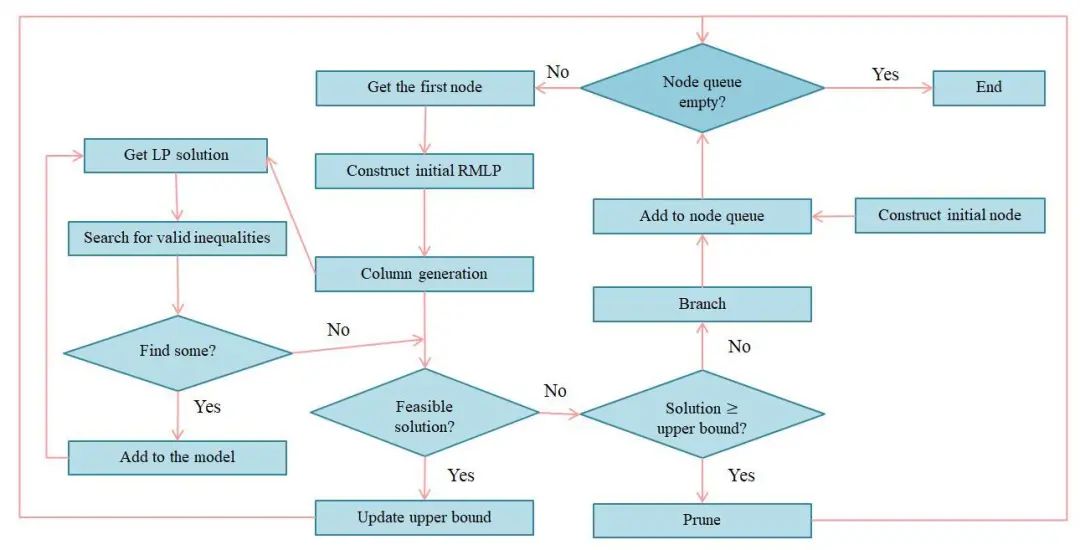
接下来我们基于上图,代入到SDVRPTW模型的求解进行阐述。从图片右上方开始,我们首先构造一个初始的分支定界树的结点,并将该结点加入到搜索队列。当搜索队列不为空时,对队列头结点开始迭代求解。
对MP进行松弛,构造一个求解表达式(16)-(20)和(23)的约束线性主问题(Restricted linear master problem,RLMP),RLMP虽然与松弛后的MP(称为LMP)有相同的约束,但是只包含了部分有限的决策变量。然后开始列生成迭代。通过前面推文的复习,我们知道在列生成过程中,核心就是通过定义求解Subproblem(也有叫pricing problem),寻找除了RLMP包含的变量外,LMP是否还存在负检验数的变量θ_rw。Subproblem的符号定义如下:

综上建立如下Subproblem模型:
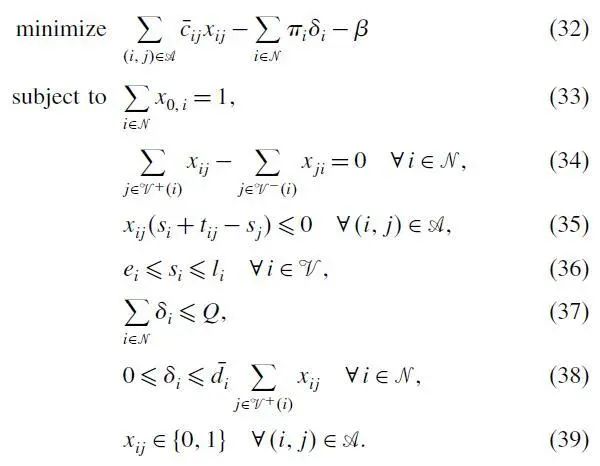
其中,
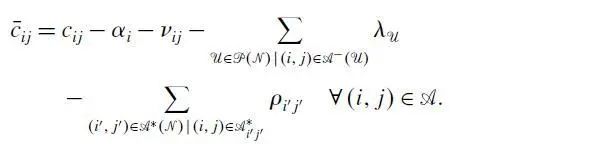
本文的Subproblem是一个有界背包问题,这里Desaulniers(2010)采用labeling algorithm进行精确求解。当找不到检验数为负的列(路径),则停止列生成得到当前RLMP的最优解,对应算法流程图的LP solution,否则添加找到的负列到RLMP中,继续调用列生成迭代。
将上述过程最终得到的LP solution作为当前分支定界树节点的下界,并通过引进违反的有效不等式作为Cuts,加入到当前RLMP的约束中,再调用列生成过程改进下界,直到找不到违反的Cuts时停止列生成迭代,得到改进后的下界,则算法需要判断以下三种情况:
如果改进后的下界大于等于当前最优上界,则节点被剪枝;
如果改进后的下界小于当前最优上界,且为整数解,则更新为当前最优上界;
如果改进后的下界小于当前最优上界,但不是整数解,则通过一系列branching decision对节点进行分支,得到的结点加入到搜索队列等待后续搜索。
当搜索队列为空,即所有搜索节点都被搜索完毕后时,算法停止,框架下界值即为最优解。
小声吐槽:以上步骤希望读者结合前言的推文回顾,仔细阅读,定可以对其他涉及BPC的论文进行举一反三。小编也是学了很久才搞明白。
4
相关研究及问题变式
Archetti et al. (2011)在Dsaulniers(2010)模型的基础上改进了BPC算法。因为使用精确算法求解Subproblem比较慢,所以作者先用Tabu Search寻找负检验数的列,如果找不到再调用labeling algorithm,同时引进了更多类型的Cuts改善下界,使用启发式separation algorithm寻找违反的有效不等式。以上技术都加快了BPC对SDVRPTW的求解速度。
Salani and Vacca(2011)研究了discrete SDVRPTW,在这个问题中,客户的需求为一系列可以分别配送的离散物品,且在客户点的服务时间正比于配送量。因为这个特征,前文提到的性质不再有效,比如实例的解允许两条路径有超过一个相同客户是分批交货的。
Luo et al.(2017)研究了SDVRPTW with linear weight-related cost,在这个问题中,每单位距离的行驶成本是车辆载重的线性函数。本文的labeling algorithm更加高效,虽然每个标签的定义都包含了检验数与车辆载重之间的函数关系,因此每个顶点可能生成的标签数量将会是Desaulniers(2010)的三倍,但因为使用了一对多的dominance rule,所以最后保留下来的标签数量将会变少,且性质更优,这也得益于作者提出了一个dominance graph。
Archett et al.(2011)首次用BPC解决SDVRP,即问题去掉了对客户时间窗的约束。模型和算法都与Desaulniers(2010)相似,主要区别是在求解Subproblem时,将每个客户点转化为一系列该客户可能配送量的点,再利用labeling algorithm求解时将变得简单,但因此算法的效率也极大的取决于客户需求的规模。

所有文献下载链接见评论区。
5
参考文献
[1] Desaulniers G (2010) Branch-and-price-and-cut for the split delivery vehicle routing problem with time windows. Oper.
Res. 58(1):179–192.
[2] Archetti C, Bouchard M, Desaulniers G (2011) Enhanced branch and price and cut for vehicle routing with split deliveries and time windows. Transportation Sci. 45(3):285–298.
[3] Salani M, Vacca I (2011) Branch and price for the vehicle routing problem with discrete split deliveries and time windows. Eur. J. Oper. Res. 213(3):470–477.
[4] Luo Z, Qin H, Zhu W, Lim A (2017) Branch and price and cut for the split-delivery vehicle routing problem with time windows and linear weight-related cost. Transportation Sci. 51(2):668–687.
[5] Archetti C, Bianchessi N, Speranza MG (2011) A column generation approach for the split delivery vehicle routing problem. Networks. 58(4):241–254.
[6] 舒胜男. 求解多周期质检员排期问题的精确算法设计[D]. 武汉:华中科技大学. 2017
THE
END
文案编辑:苏锷,华中科技大学管理学院,sue61239101@qq.com
指导老师:秦虎,华中科技大学管理学院,professor.qin@qq.com
