干货 | 求解VRPTW松弛模型的Column Generation算法的JAVA代码分享

前言

经过小编的不断努力和修正，Column Generation + ESPPRC+ pulse algorithm的内容终于写完了。此过程真是充满曲折啊，希望大家看完多多支持一下。

运行说明

关于这部分的代码，我们提供两个版本。

第一个版本来自GitHub，是一个叫Seminar的国外大神写的。

他的子问题采用上一篇推文介绍的模型，找一条reduced cost最短的路径，运行只需要更改下面文件中算例文件的路径即可。

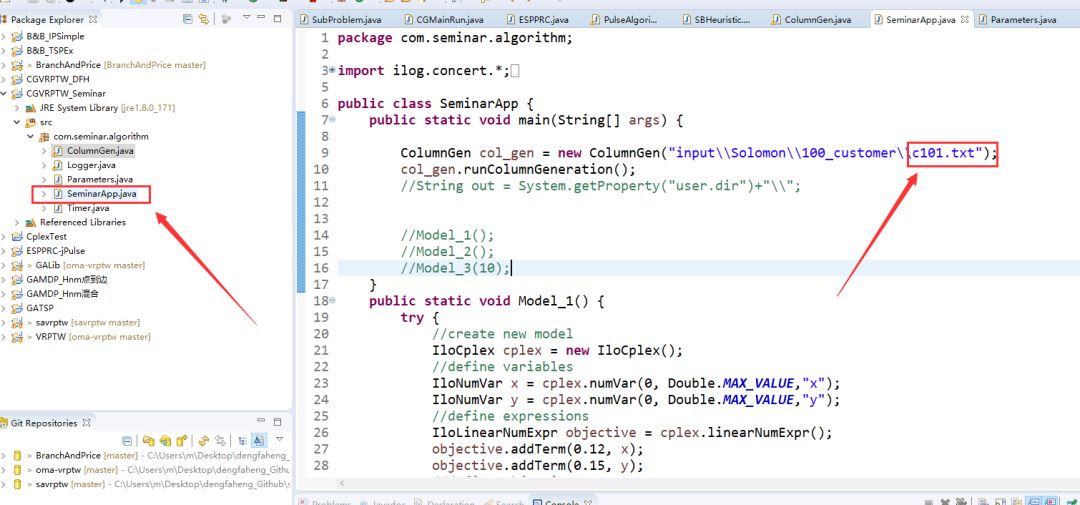
运行的中间结果如下：

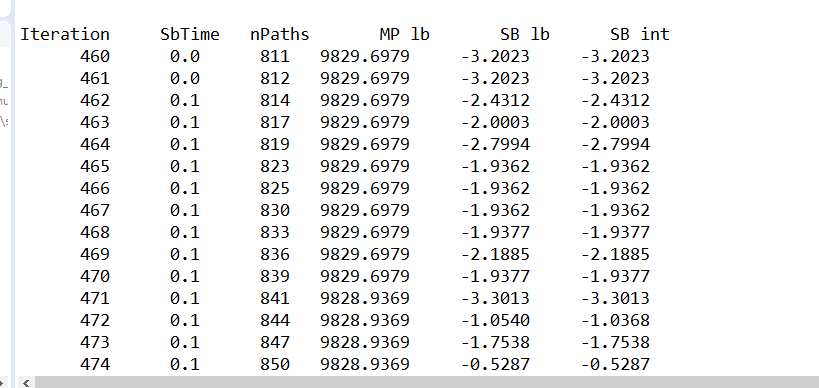
- Iteration：迭代次数

- SbTime：子问题求解时间(s)

- nPaths：Master Problem中的总路径

- MP lb：Master Problem的线性松弛最优解，这里由于建模方式的原因，该最优解把服务时间也算在路径距离上的，最终减去9000即可得到路径距离。

- SB lb：子问题的线性松弛最优解。

- SB int：子问题的整数最优解。

关于子问题的最大求解时间限制(s)，可以在下面文件中设置：

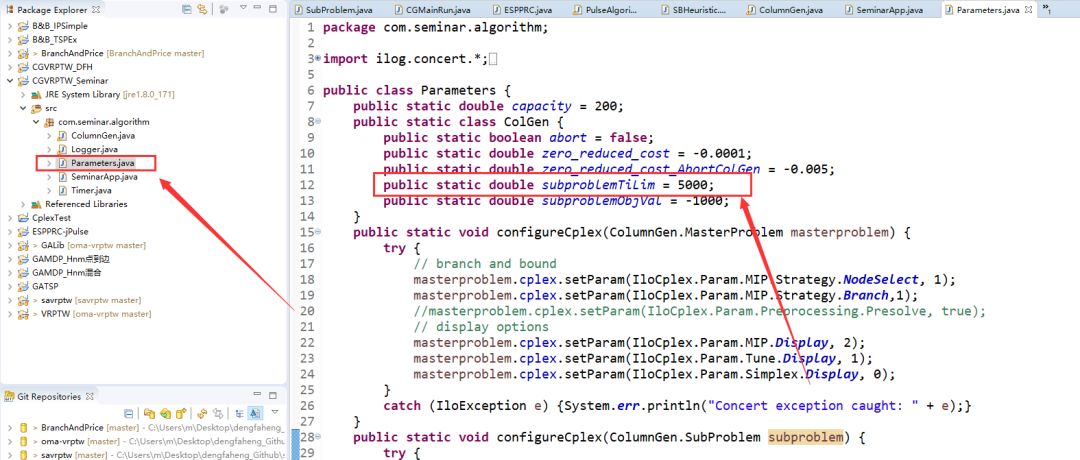
第二个版本是小编写的：

运行参数说明：

-in：算例文件路径；

-out：结果文件输出。

比如：

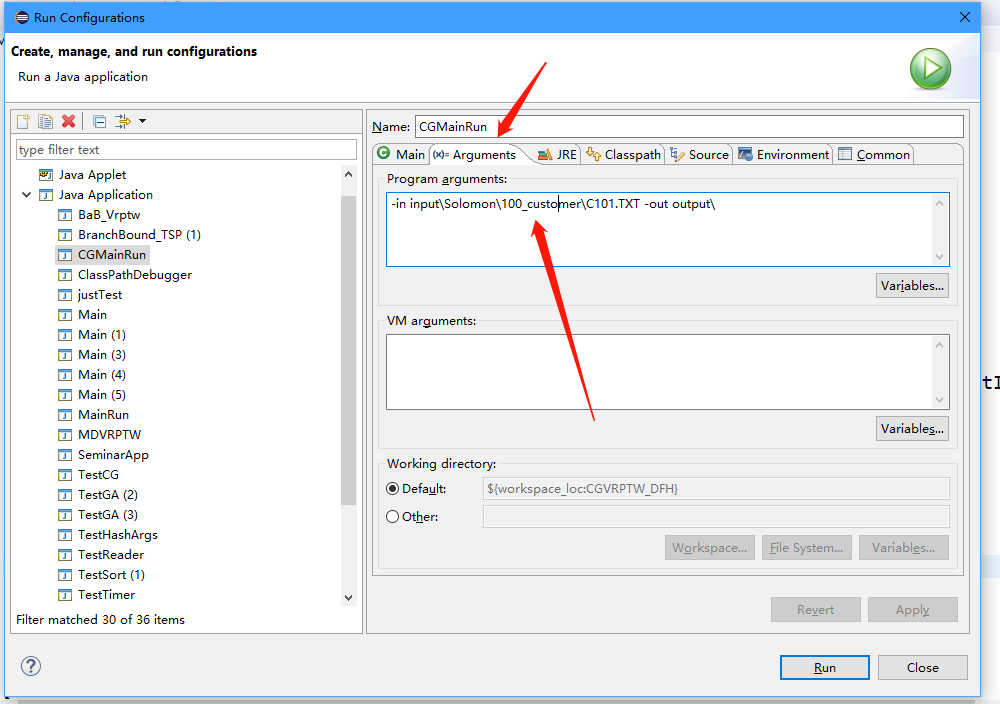
【-in input\Solomon\100_customer\C101.TXT -out output\】

参数设置请找到以下主运行文件：

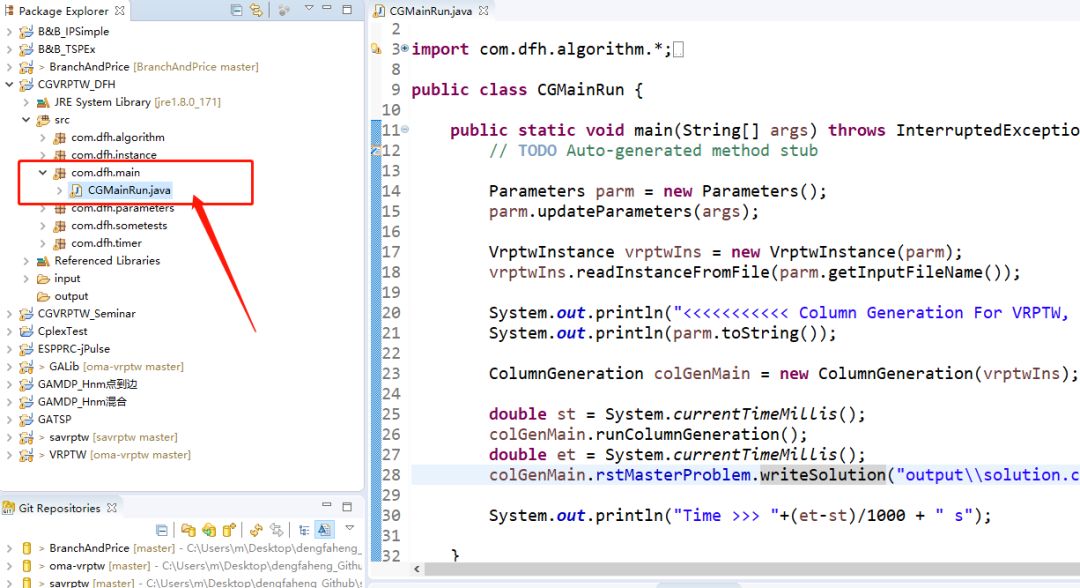
右键找到运行设置里面进行配置。（默认情况下输入上面的参数能直接运行）

中间结果：

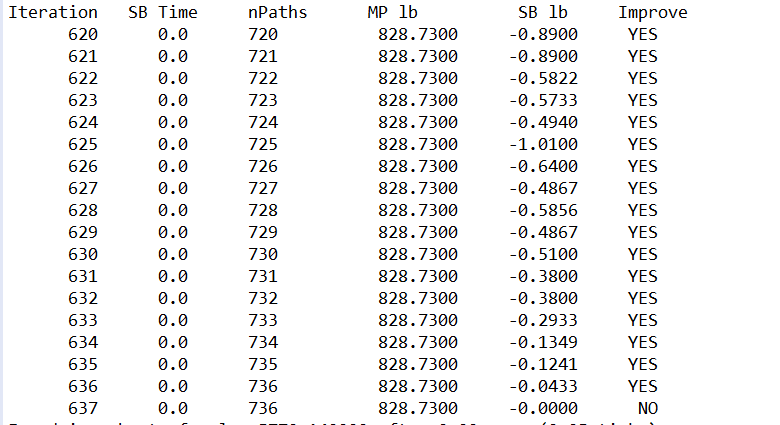
- Iteration：迭代次数

- SbTime：子问题求解时间(s)

- nPaths：MasterProblem中的总路径

- MP lb：Master Problem的线性松弛最优解。

- SB lb：子问题的最优解。

关于第一个版本，其子问题建模方式还是依赖主问题的对偶变量的，如下：

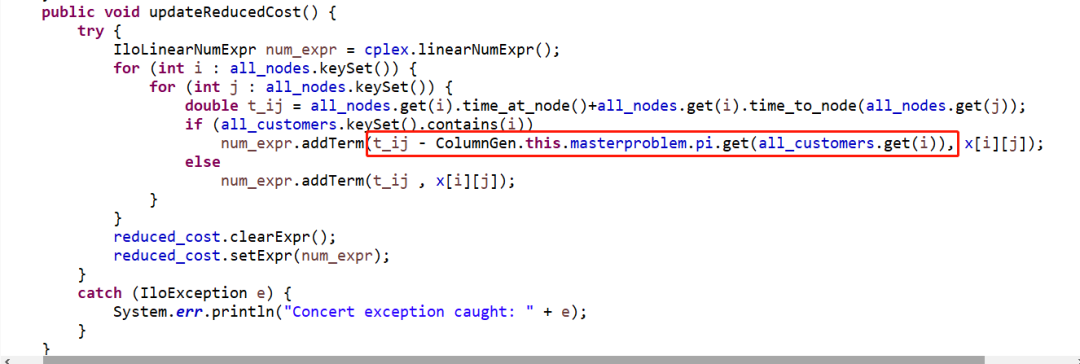
其中t_ij就是每条边本来的cost，pi就是Master Problem的对偶变量。每一次迭代就是这样更新子问题的cost，重新建模求解的。

关于小编的版本：

每次迭代的时候会更新ESPPRC问题中的cost，然后运行pulse算法重新求解。

其他的话结构和注释都写得非常清晰了，大家肯定能看懂的。

由于是精确算法，子问题时间没有保障的，有时候很快能跑完，有时候一天都跑不完。和算例有很大关系的。

【如对代码有疑问，可联系小编，可以提供有偿辅导服务】

【有偿辅导纯属个人行为，与团队无关】

代码获取

代码获取请关注我们的公众号，在公众号后台回复【cgvrptw】不包括【】即可获取。

觉得不错的同学请在GitHub上加个星，谢谢！

END