干货 | VRPTW子问题ESPPRC的介绍及其求解算法的C++代码
wake up

各位小伙伴大家好,相信大家已经看过前面Column Generation求解VRPTW的线性松弛模型的过程详解了。
子问题的目标是找到一条reduced cost最小的合法路径,然后加入到Linear Master Problem中。其实,子问题被称为Elementary Shortest Path Problem with Resource Constraints (ESPPRC)也是一个著名的NP-Hard问题,今天我们就来详细介绍一下。


01 ESPPRC

考虑图1.1中描述的网络。除了每条边的成本c_ij之外,还存在经过边(i,j)的所消耗的资源t_ij,比如时间。我们的目标是找到从开始节点到结束节点的最短路径,每个节点只能访问一次,同时使得资源消耗满足可用的资源约束,比如全程不能超过多少时间[1]。
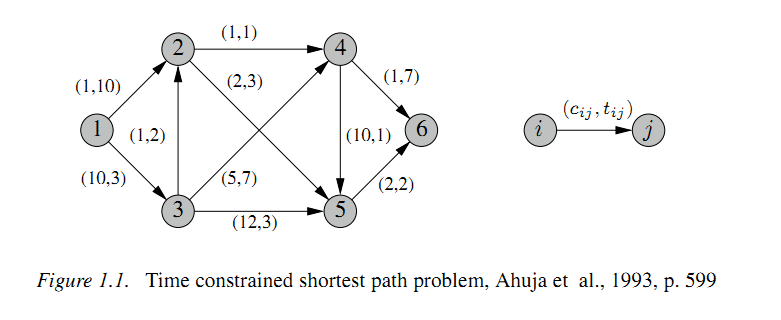
当然上面描述问题只是ESPPRC中的一个例子,实际的资源约束可能有很多种,比如在VRPTW的子问题中[2]:
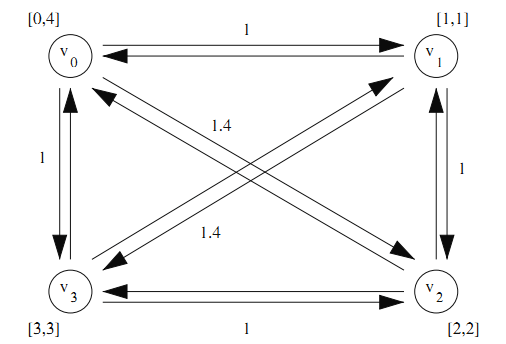
起始节点和结束节点一样,每个节点有固定的时间窗和固定的需求,车辆不能超过容量约束的要求等等。
ESPPRC vs SPPRC
SPPRC和ESPPRC一样,只不过SPPRC去掉了elementary的约束,允许最短路中一个节点被访问多次。
02 应用

我们知道,ESPPRC可以应用在Column Generation中的算法框架中的。那么具体是怎么应用的呢?
我们知道,在Column Generation中,子问题每次迭代就是找一条reduced cost最小的路径,然后加入到Master Problem中。但是对于ESPPRC来说,每次的cost一样的,那不每次都求出同一条路径吗???
不!在Column Generation中,其子问题ESPPRC中边的cost是会随着Linear Master Problem的对偶变量值的改变而改变的。还记得reduced cost是怎么计算的吗?

其中,式子(22)可以表达成式子(23)。(23)是什么意思呢?b_ijk意思是边ij是否在路径k中。
那么,在每一次迭代中,我们就可以利用Linear Master Problem的对偶变量,来更新ESPPRC中每条边的cost,最终求得的路径cost就是Column Generation中的reduced cost。
03 常见的算法

ESPPRC的建模如下[4]:


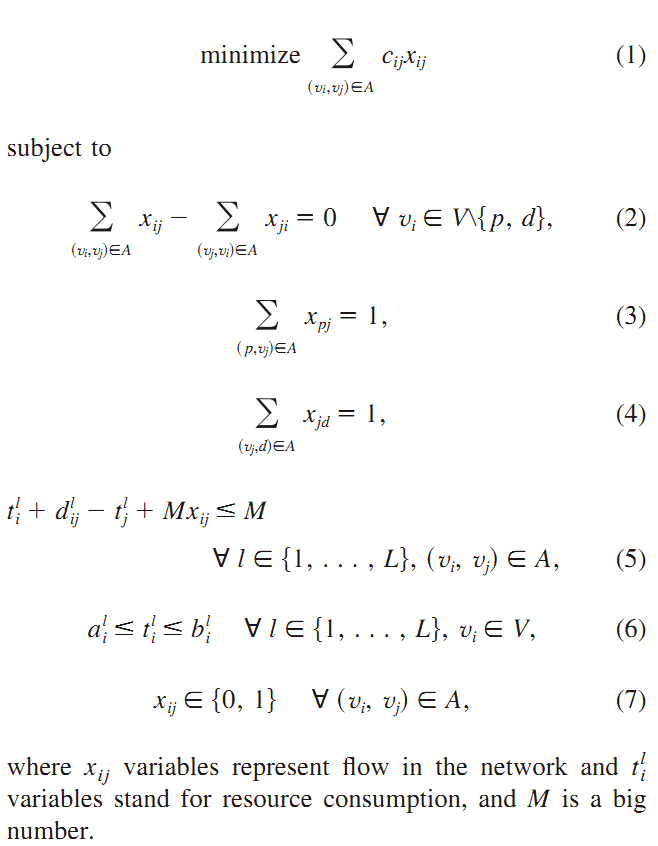
求解SPPRC和ESPPRC常见的算法主要有以下几种[3]:
Dynamic programming and labeling algorithms
Lagrangean relaxation
Constraint programming(建模)
Heuristics
04 Pulse Algo

这一节介绍一个ESPPRC的精确算法Pulse Algorithm[5],算法的伪代码如下:

其中:
r:表示到达当前节点时的cost;
q:表示到达当前节点时的装载量;
t:表示到达当前节点所需的总时间,早到需要等待,不能晚到。
大体的思想是通过bound算法确定到达每个节点的最低cost,然后pulse进行路径搜索,而之前bound求出来的最低cost就可以在pulse搜索的过程中起到定界的作用,去掉一些不好的路径。
bound的算法如下:

每个节点的最低cost(相当于一个lower bound)是怎么算出来的呢?简单来说是通过限定每个节点最晚到达时间。
在每个节点都给定最晚到达时间t,然后计算在这个最晚到达时间下,每个到达每个节点的最低cost。
然后让t递减,直到t减少到临界值。最终得到的是每个节点关于各个最晚到达时间的最低cost矩阵。
最后来看看pulse算法:

pulse是找路的过程,在该过程中:
isFeasible检查到达节点时路径是否满足各种资源约束。
checkBounds检查在当前到达时间下,到达节点的cost是否小于等于之前bound算法求出来的那个最晚时间下的最低cost,如果不是就丢弃该支路径。
rollback进行如下检查:
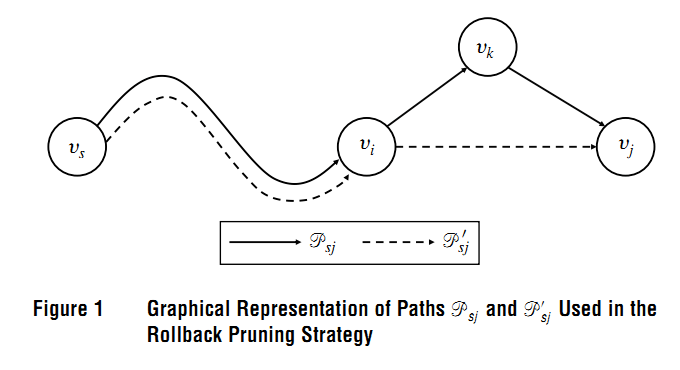
在每一个节点(开始节点除外),比如上图中节点j,如果实线路径的cost < 虚线路径的cost。那么砍掉实线的路径(已经有人的cost比你更低,你可以卷铺盖走人了),这就相当于一个回滚的操作,回滚到节点i的状态,然后直接走虚线路径。

以上就是整个pulse算法。这里只是起到一个抛砖引玉的过程。可能讲的不是很详细,详细的过程请大家去阅读文献。
05 算法代码

关于整个pulse算法伪代码和讲解已经够详细了,这里给出一个C++的实现代码,是我远房的一个学长的学姐的男朋友写的(真话)。关于编译运行上面也说明得够详细了。
代码下载请移步留言区。
【如对代码有疑问,可联系小编,可以提供有偿辅导服务】

References
[1] Desrosiers J , Marco E. Lübbecke. A Primer in Column Generation. Column Generation, G. Desaulniers, J. Desrosiers, and M.M. Solomon (Eds.), Springer, 2005.
[2] Feillet D . A tutorial on column generation and branch-and-price for vehicle routing problems. 4OR: A Quarterly Journal of Operations Research, 2010, 8(4):407-424.
[3] Irnich S . Shortest Path Problems with Resource Constraints. Column Generation, G. Desaulniers, J. Desrosiers, and M.M. Solomon (Eds.), Springer, 2005.
[4] Feillet D , Dejax P , Gendreau M , et al. An exact algorithm for the elementary shortest path problem with resource constraints: Application to some vehicle routing problems. Networks, 2004, 44(3):216-229.
[5] Leonardo Lozano, Daniel Duque, Andrés L. Medaglia (2016) An Exact Algorithm for the Elementary Shortest Path Problem with Resource Constraints. Transportation Science 50(1):348-357.
END
