一文详解变分自动编码器（VAE）
大数据文摘授权转载自数据派THU
作者：赵健愚
校对：汪雨晴
变分自动编码器（Variational autoEncoder，VAE）是生成模型的一种。这些方法的主要目标是从对象的学习分布中生成新的采样数据。2014 年，Kingma et al. [3]提出了这种生成模型，该模型可以从隐变量空间的概率分布中学习潜在属性并构造新的元素。
VAE 概述
VAE 包含两个部分：编码器 encoder 和解码器 decoder。如图 1 所示，编码器计算每个输入数据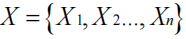
的低维均值μ和方差
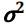，然后从隐变量空间采样，得到Z={Z1,Z ...,Zn}，通过解码器生成新数据Y ={Y1,Y2...,Yn}。我们希望从隐变量空间中的采样的数据 Z 遵循原始数据 X 的概率分布，这样我们根据采样数据 Z 生成的新数据 Y也就可以遵循原始数据的概率分布[2]。
概率分布
但是问题来了，如何才能保证采样数据 Z 的概率分布是符合输入 X 的呢？首先假设存在一个 Z 关于 X 的后验后验概率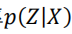
，并进一步假设这个概率分布是正态分布：
p(Z | X ) = N(0, I)
那么采样数据 Z 的概率分布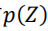
就为：
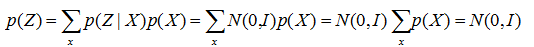
这样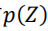 (先验分布)和 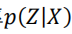(后验分布)就都符合标准正态分布了。
损失函数
VAE 生成图片的性能可以通过 evidence lower bound（ELBO) loss 来评估，该损失由Reconstruction loss 和 Kullback–Leibler loss（KL loss）组成。Reconstruction loss 用于计算生成的数据与原始数据的相似程度，而 KL loss 作为一个额外的 loss，用于测量一般正态分布与标准正态分布的差异，也就是均值 μ 和方差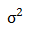
之间的差异[1][4]。
在给定的隐变量空间维度为 n 的条件下，已知均值 μ 和方差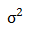，KL loss 定义为:
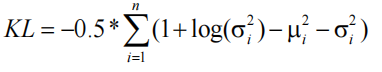
Reconstruction loss 在这里可以使用标准的 L2 Loss 也就是 MSE。给定 m 个数据，已知真实值 x 和预测值X^。Reconstruction loss 定义为：
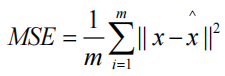
最终，ELBO loss 由上述两个损失函数组成，系数为 α 和 β：
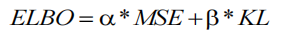
简单来说，这里的 Reconstruction loss 是用来让 decoder 的输出 Y 和输入 X 尽可能相似。而 KL loss 希望隐变量空间可以符合标准的正态分布，但实际 X 的分布其实并不是标准的正态分布，也就是说 KL loss 会让输出 Y 具有多样性，与输入 X 产生一部分的差异。
在 MATLAB 的实例中[4]，Reconstruction loss 和 KL loss 的比例是 1：1，这样既能保证生成图像的质量，又可以引入一定的噪声，使生成图片有一定的泛化能力。关于ELBO Loss 的具体实现如下所示：
Fig. 2. ELBO loss in the MATLAB example.
在图 2 所示代码中，方差是用log (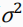
)表示的，这是因为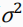的结果永远是非负的，在神经网络拟合的过程中需要加激活函数，但是log (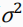)的结果可正可负，可以不加激活函数处理。
重参数技巧
除了这个特殊的损失函数，作者还介绍了一种名为重参数技巧（Reparameterization
trick）的方法。
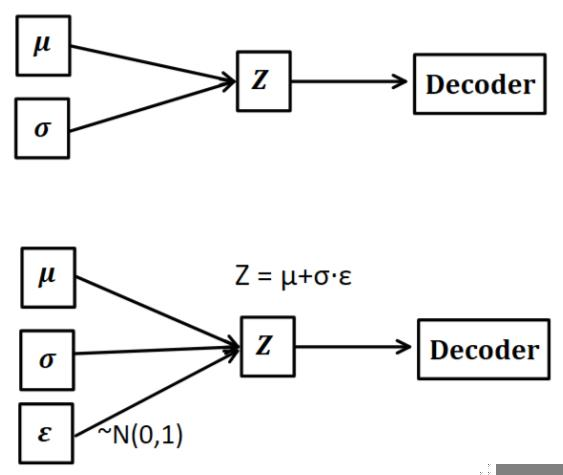
Fig. 3. Reparameterization trick.
正因为我们假设 p(Z | X ) = N(0, I) , 但是均值和方差都是靠 encoder 计算出来的，然后我们要靠这个均值和方差反向优化 encoder。但是随机采样这个操作是不可导的，我们不可能通过随机采样操作进行反向传播。因此我们可以利用随机采样的结果，本来我们需要从均值和方差的分布中随机采样，现在我们只需要生成一组符合正态分布的变量ε。如图 3 所示，从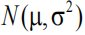
中采样一个 Z，相当于从 N(0,I) 中采样一个 ε，然后让
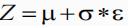。这样随机采样就不用参与梯度下降了，只需要更新采样的结果。图 4 的示例代码展示了如何从 encoder 中采样并且进行重参数技巧：
Fig. 4. Sampling function in the MATLAB example.
维度对 VAE 的影响
在变分自编码器中，隐变量空间的维度（dimensionality）是一个非常重要的变量，在一般的编码器（AE）中，这个变量也被称为 bottleneck。如果给定 m 个数据，维度的大小为 n，那么每个数据就会产生 n 个均值和 n 个方差。不同的维度会导致 decoder 生成不同的图片，我们这里使用 MNIST 的训练集，在ELBO = 0.5*MSE + 0.5*KL的情况下来训练变分自动编码器，用 MNIST 的测试集来测试重构的效果。如图 5，在维度为 2，5，10，20 的情况下，左边图片代表 ground truth，也就是 encoder 的输入，右边图片代表生成的图片，也就是 decoder 的输出。
Fig. 5. Comparison between the ground truth digits and the reconstruction based on different dimensionality.
我们可以看出，在隐变量空间的维度较低时，生成的数字较为模糊，在隐变量空间的维度较高时，生成的数字相对而言噪声小，更加清晰，并且与原图像有着一定的相似度。
损失函数对 VAE 的影响
从第五节可以看出，不同维度的大小会影响生成图片的质量。同样的，不同的损失函数也会导致 VAE 生成不同质量的图片。在第三节的最后一段我们提到过，Reconstruction loss 希望输出和输出保持相同，而 KL loss 在原有的基础上引入了一定的噪声。因此，我们可以通过修改两个损失函数的权重，来控制不同的损失函数对输出的影响程度。在 0.1*MSE + 0.9*KL 0.9*MSE + 0.1*KL 的情况下，生成的图片又会有什么差别呢？图 6 展示了不同损失函数下生成图片的质量（隐变量空间维度为 20），就像我们想得那样，在 MSE 权重较大的情况下，生成的图片几乎与原图片一模一样，几乎没有噪声。而在 KL loss 占主导时，生成的图片由于噪声过大已经完全看不出来是什么了。
Fig. 6. Comparison between the ground truth digits and the reconstruction based on different loss function.
除了观察生成的图片的质量，我们还可以通过对隐变量空间的分析来查看数据的分布情况。当 MSE 权重较大的时候（0.9*MSE + 0.1*KL），隐变量空间的分布情况更像原数据的分布情况，我们通过使用 t-SNE 降维[5]分析均值（代码见图 7），可以得到如图8 所示的聚类图。这里每组数据的标签使用的原数字的标签。显然，隐变量空间均值的分布情况与原数据的分布情况（数字 0-9 的聚类）几乎一样。当然了，由于我们保留了一定的 KL loss，采样过程中引入了一定的噪声，每组聚类的周围会有一些 outliers。
Fig. 7. Code for t-SNE clustering based on the mean.
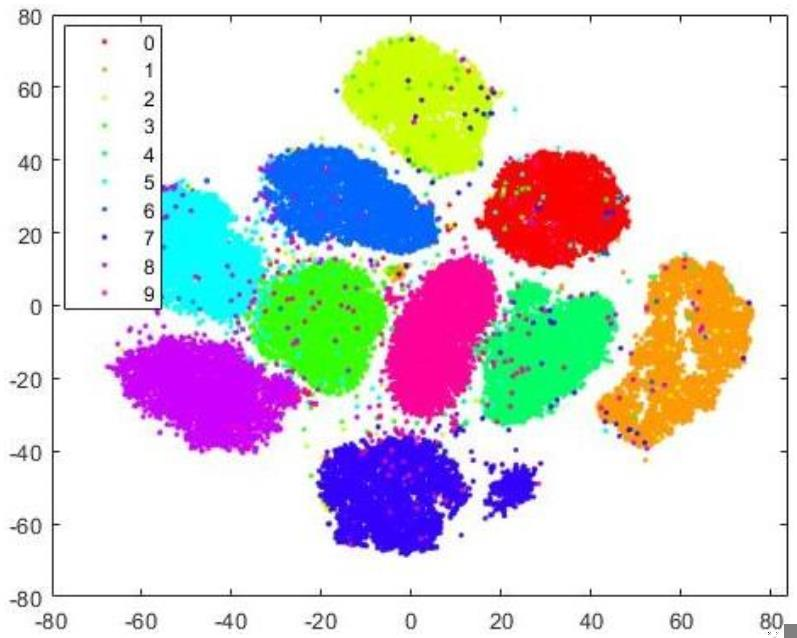
Fig. 8. Clusters generated by t-SNE based on the mean，ELBO = 0.9 ∗ MSE + 0.1 ∗ KL.
类似的，在0.1*MSE + 0.9*KL的情况下，由于隐变量空间的均值被拟合为正态分布，它很难反映出原数据的分布情况，如图 9。
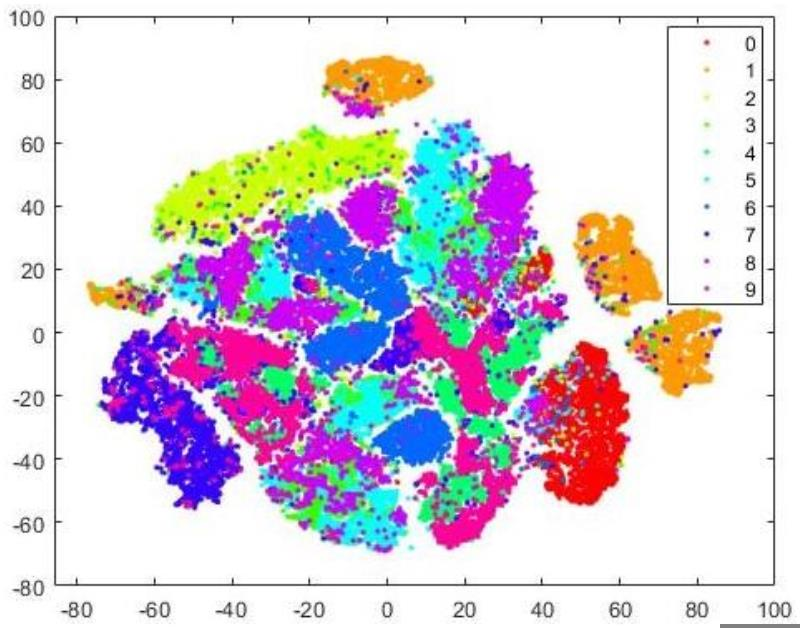
Fig. 9. Clusters generated by t-SNE based on the mean，ELBO = 0.1 ∗ MSE + 0.9 ∗ KL.
总结
尽管 VAE 在名字上很像 AE（自动编码器），但其方法（或其对网络的解释）是独特的。在 VAE 中 ，encoder 用于计算平均值和方差，这与平时的 AE 完全不是一个类型的模型。对于不同的隐变量空间维度，VAE 具有不同的性能，相对而言，隐变量空间越大，可以保留的概率分布的信息就越多。但我们并不能说，隐变量空间越大就一定越好，考虑一个极限的情况就是当输入图片是 28*28*1 的情况下，隐变量空间的大小设置为 784，也就是原数据的大小，VAE 也就失去了 encoding 的意义了。
对于损失函数 ELBO loss，我们可以调整它的权重来达到不同的生成效果，毕竟我们在生活中也会遇到相当多的噪声，这对于模型的鲁棒性来说是非常有意义的。
除了VAE，后续还有很多类似的模型比如条件变分自编码器
（Conditional VariationalautoEncoder），生成对抗编码器（VAEGAN）等等，这个领域的不断发展也带了更更好的生成类模型，感兴趣的同学可以去搜一搜论文，或者直接运行 MATLAB 中的实例跑一跑，修改参数做一些实验，或许下一个发明 VAE 的人就是你。
Reference：
1. Bishop, C.M., 2006. Pattern recognition and machine learning. springer. pp. 55–58.
2.Doersch, C., 2016. Tutorial on variational autoencoders. arXiv preprintarXiv:1606.05908.
3. Kingma, D.P. and Welling, M., 2013. Auto-encoding variational bayes. arXiv
preprint arXiv:1312.6114.
4. MathWorks, “Train Variational Autoencoder (VAE) to Generate Images”,
https://www.mathworks.com/help/deeplearning/ug/trainavariationalautoencoder-vae-to-generate-images.html (accessed Sep. 5, 2021).
5. Van der Maaten, L. and Hinton, G., 2008. Visualizing data using t-SNE. Journal ofmachine learning research, 9(11).
