「本文概览」

今天给大家介绍一篇VAEs用于推荐系统召回侧的文章，论文题目为《Variational Autoencoders for Collaborative Filtering》。VAEs (Variational Autoencoders 变分自编码器) 是一类基于变分推断和 Encoder-Decoder 结构的生成式模型。这一类模型具有较强的表征能力，其 latent space 的性质也让 VAEs 在很多下游任务中有较好的应用。本文是VAEs模型在协同过滤中的使用，非线性的概率模型大大提升生了模型的表征能力。

• 引用：Liang D, Krishnan R G, Hoffman M D, et al. Variational autoencoders for collaborative filtering[C]//Proceedings of the 2018 world wide web conference. 2018: 689-698.
• 论文下载地址：https://dl.acm.org/doi/pdf/10.1145/3178876.3186150
• 论文源码：https://github.com/dawenl/vae_cf

1. 背景知识

1.1 AutoEncoder(AE)

如下图所示，AutoEncoder框架包含两大模块：编码过程和解码过程。通过 encoder(g) 将输入样本 映射到特征空间 ，即编码过程；然后再通过 decoder(f) 将抽象特征 映射回原始空间得到重构样本 ，即解码过程。优化目标则是通过最小化重构误差来同时优化encoder和decoder，从而学习得到针对输入样本 的抽象特征表示 。

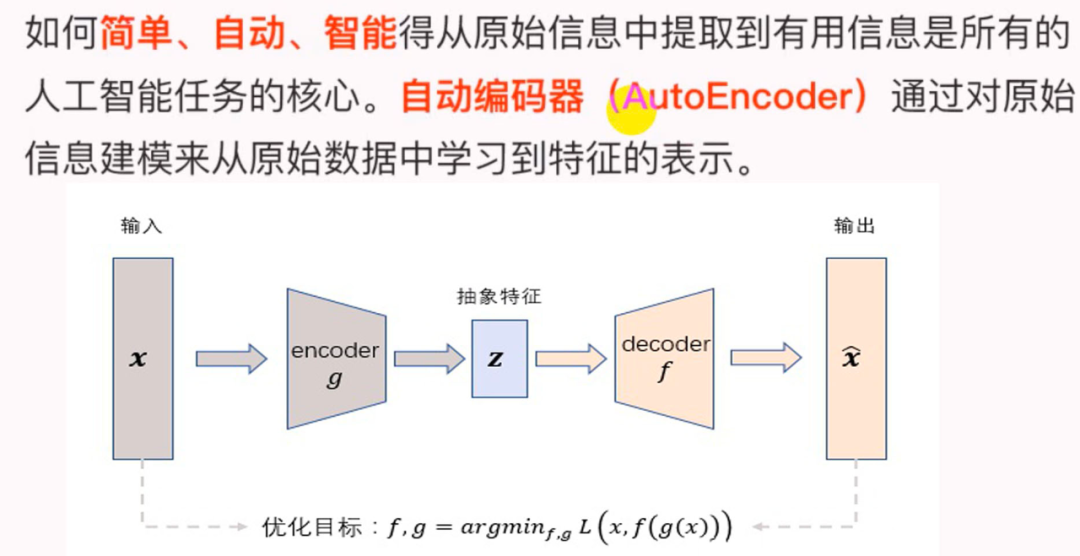
这里我们可以看到，AutoEncoder在优化过程中无需使用样本的label，本质上是把样本的输入同时作为神经网络的输入和输出，通过最小化重构误差希望学习到样本的抽象特征表示 。这种无监督的优化方式大大提升了模型的通用性。

对于基于神经网络的AutoEncoder模型来说，则是encoder部分通过逐层降低神经元个数来对数据进行压缩；decoder部分基于数据的抽象表示逐层提升神经元数量，最终实现对输入样本的重构。

这里值得注意的是，由于AutoEncoder通过神经网络来学习每个样本的唯一抽象表示，这会带来一个问题：当神经网络的参数复杂到一定程度时AutoEncoder很容易存在过拟合的风险。

1.2 Denoising AutoEncoder(DAE)

为了缓解经典AutoEncoder容易过拟合的问题，一个办法是在输入中加入随机噪声，Vincent等人提出了Denoising AutoEncoder，即在传统AutoEncoder输入层加入随机噪声来增强模型的鲁棒性；另一个办法就是结合正则化思想，Rifai等人提出了Contractive AutoEncoder，通过在AutoEncoder目标函数中加上Encoder的Jacobian矩阵范式来约束使得Encoder能够学到具有抗干扰的抽象特征。

下图是Denoising AutoEncoder的模型框架。目前添加噪声的方式大多分为两种：

• 添加服从特定分布的随机噪声；
• 随机将输入 中特定比例的数值置为0；

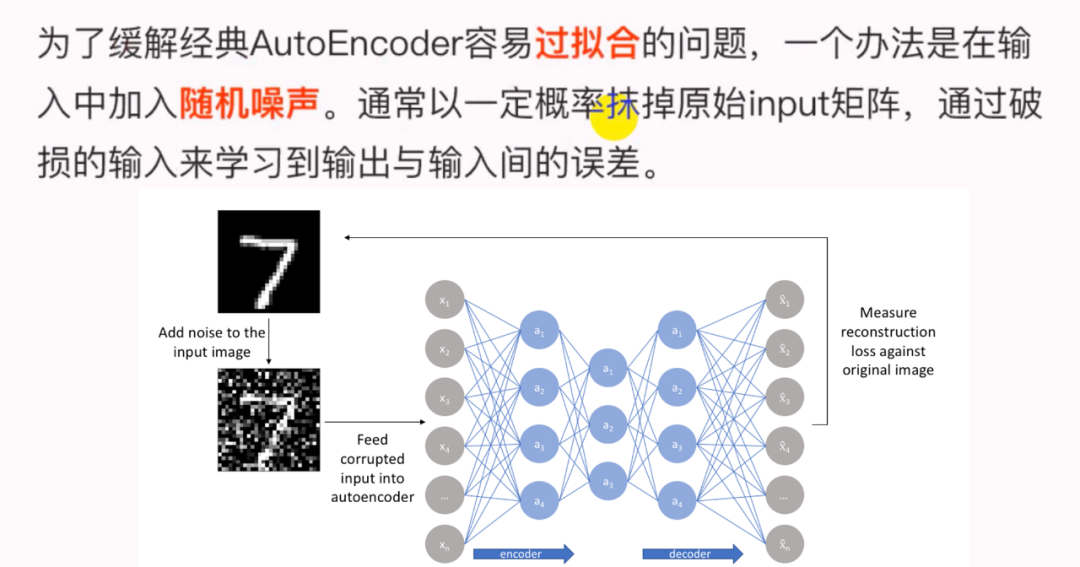
DAE模型的优势：

• 通过与非破损数据训练的对比，破损数据训练出来的Weight噪声较小。因为擦除数据的时候不小心把输入噪声给擦掉了。
• 破损数据一定程度上减轻了训练数据与测试数据的代沟。由于数据的部分被擦掉了，因而这破损数据一定程度上比较接近测试数据。

1.3 简介Variational Autoencoders(VAEs)

变分自编码器是自动编码器的升级版本，其结构跟自动编码器是类似的，也由编码器和解码器构成。

在自动编码器中，我们需要输入一张图片，然后将一张图片编码之后得到一个隐含向量，这个隐含向量比我们随机取一个随机噪声更好，因为它包含着原图片的信息，然后我们把隐含向量解码得到与原图片对应的照片。

但是这样我们并不能任意生成图片，因为没有办法自己去构造隐含向量，需要通过一张图片输入编码，才知道得到的隐含向量是什么。这时我们就可以通过变分自编码器来解决这个问题。

其实原理特别简单，只需要在编码的过程中给它增加一些限制，迫使其生成的隐含向量能够粗略的遵循一个标准正态分布，这就是其与一般的自动编码器最大的不同。

这样我们生成一张新图片就很简单了，只需要给它一个标准正态分布的随机隐含向量，这样通过解码器就能够生成我们想要的图片，而不需要给它一张原始图片先编码。

在实际情况中，我们需要在模型的准确率上与隐含向量服从标准正态分布之间做一个权衡。所谓模型的准确率就是指解码器生成的图片与原图片的相似程度。另外要衡量两种分布的相似程度，有一个东西叫KL divergence来衡量两种分布的相似程度，这里我们就是用KL divergence来表示隐含向量与标准正态分布之间差异的loss。我们让网络自己来做决定如何权衡，非常简单，我们只需要将这两者分别作为loss，然后再将它们求和作为总的loss，这样网络就能够自己选择如何才能够使得这个总的loss下降。

KL divergence 的公式如下：

这里变分自编码器使用了一个技巧 「“重新参数化(reparameterization)”」 来解决KL divergence的计算问题。

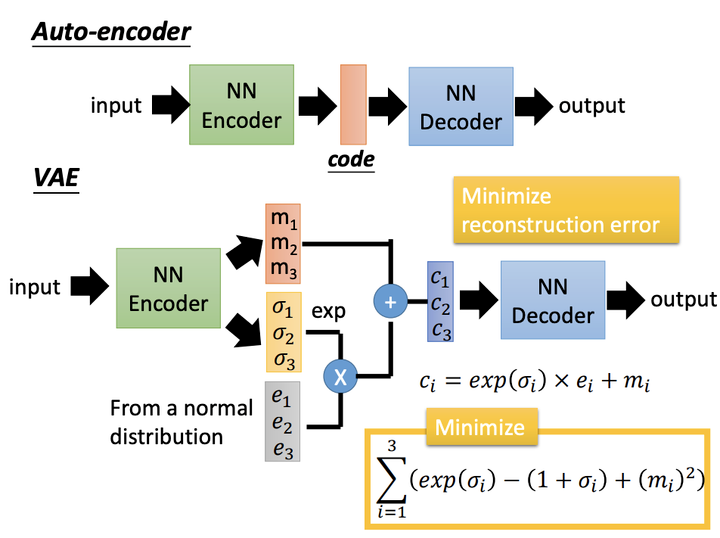
这时不再是每次产生一个隐含向量，而是生成两个向量，一个表示均值 ，一个表示标准差 ，然后通过这两个统计量来合成隐含向量 ，这也非常简单，用一个标准正态分布 先乘上标准差再加上均值就行了，这里我们默认编码之后的隐含向量是服从一个正态分布的。这个时候我们是想让均值尽可能接近0，标准差尽可能接近1。

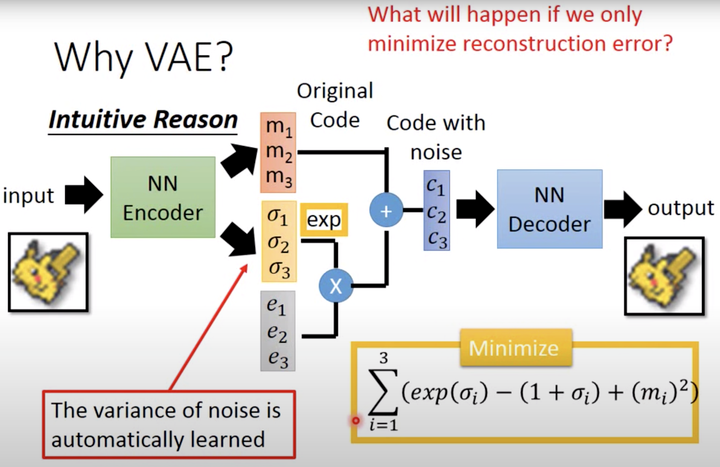
VAE通过Encoder学习出均值向量和方差向量（贝叶斯估计）。同时随机采样一个正态分布的向量 。通过 公式重采样得到 （Sampled Latent Vector），它描述的是一个潜在多元正态分布（非高斯）的均值和标准差，这个正态分布就是用来生成VAE所训练的数据。最后通过Decoder进行重建。损失函数是Decoder后的输出与初始输入的差异，以及学习后的潜在分布和先验分布之间的KL散度作为正则化， 的重参数技巧。

「【强烈推荐阅读】」

• 关于VAE的理论推导有点晦涩难懂，推荐大家观看学习李宏毅老师的教程视频。
• 关于李宏毅老师讲解的VAE视频Part1地址：https://www.youtube.com/watch?v=YNUek8ioAJk&ab_channel=Hung-yiLee
• 关于李宏毅老师讲解的VAE视频Part2地址：https://www.youtube.com/watch?v=8zomhgKrsmQ&ab_channel=Hung-yiLee
• 李宏毅老师讲解slides地址：http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2017/Lecture/GAN%20(v3).pdf

2. VAEs模型理论介绍

近年的工作，如《Neural collaborative filtering》、《Autorec: Autoencoders meet collaborative filtering》等将神经网络应用于协同过滤并取得了理想的结果。该论文将变分自编码器（Variational Autoencoders，VAEs）扩展到协同过滤。下面我们详细介绍一下VAEs模型的原理。

这一部分主要是介绍了变分自编码器 (VAEs) 的理论基础，以下部分内容参考了变分自编码器 (VAE) Overview - Zhifeng的文章 - 知乎 https://zhuanlan.zhihu.com/p/420419446

2.1 MLE、MAP、Bayesian

首先要明确这三个概念。

MLE是极大似然估计Maximum Likelihood Estimation。其目标为求解：

MAP是最大后验概率Maximum A Posteriori Estimation。其目标是求解：

这两者的区别就是在于求解最优参数时，有没有加入先验知识 。也就是MAP融入了要估计量 的先验分布在其中，因此MAP可以看做规则化的MLE。这也就解释了，为什么MLE比MAP更容易过拟合。因为MLE在求解最优 时，没有对 有先验的指导，因此 中包括了一些 的数据样本时，就会很轻易让MLE去拟合 样本。而MAP加入了对 的先验指导，例如L2正则化，那么就不易过拟合了。

举个例子，同样的逻辑回归。

• 未正则化的逻辑回归就是MLE。
• 正则化的逻辑回归就是MAP。

那么，与上述两个概念都不同的是贝叶斯模型（Bayesian Network），也被称为概率图模型。这里不是指朴素贝叶斯。而是说下面的这种学习思路。

MLE和MAP求解的都是一个最优的 值，在预测时只有最优的 参与预测过程。贝叶斯模型求解的是 的后验分布 ，而不是最大化的后验分布。因此贝叶斯模型在某种程度上可以看作是一个集成模型，在预测时，让所有 都参与预测，并将预测结果「以后验概率 作为权重进行加和作为最终预测值」。

2.2 从 MLE 到变分推断

假设数据的真实分布为 。为了训练一个生成模型，我们往往通过神经网络 构造一个复杂分布 (解码器) , 并最大化数据的 likelihood, 也就是:

但是，实际复杂的神经网络往往在数据空间进行变换，因此 没有显示的密度，直接优化 MLE 问题是不可行的。变分推断 (variational inference) 便是解决上述问题的有力工具。首先，我们引入一个新的变量称为 latent distribution (下文简写为 , 其维度远小于数据的维度)。接下来，我们定义另一个分布 , 其可以是任意的分布。由于:

我们可以将 MLE 的优化问题写成

根据 Jensen's inequality, 我们将 和 位置交换，即：

上式即为经验下界 (evidence lower bound, or ELBO)。最后，由于 可以是任意的，我们能够用一个神经网络 去逼近使得 ELBO 最大的 ， 即：

其中，可以看作VAEs模型的编码器。

由于取 的过程类似于数学中的变分法(在泛函空间中取极值)，因此该方法被称为变分推断。

2.3 VAEs网络结构

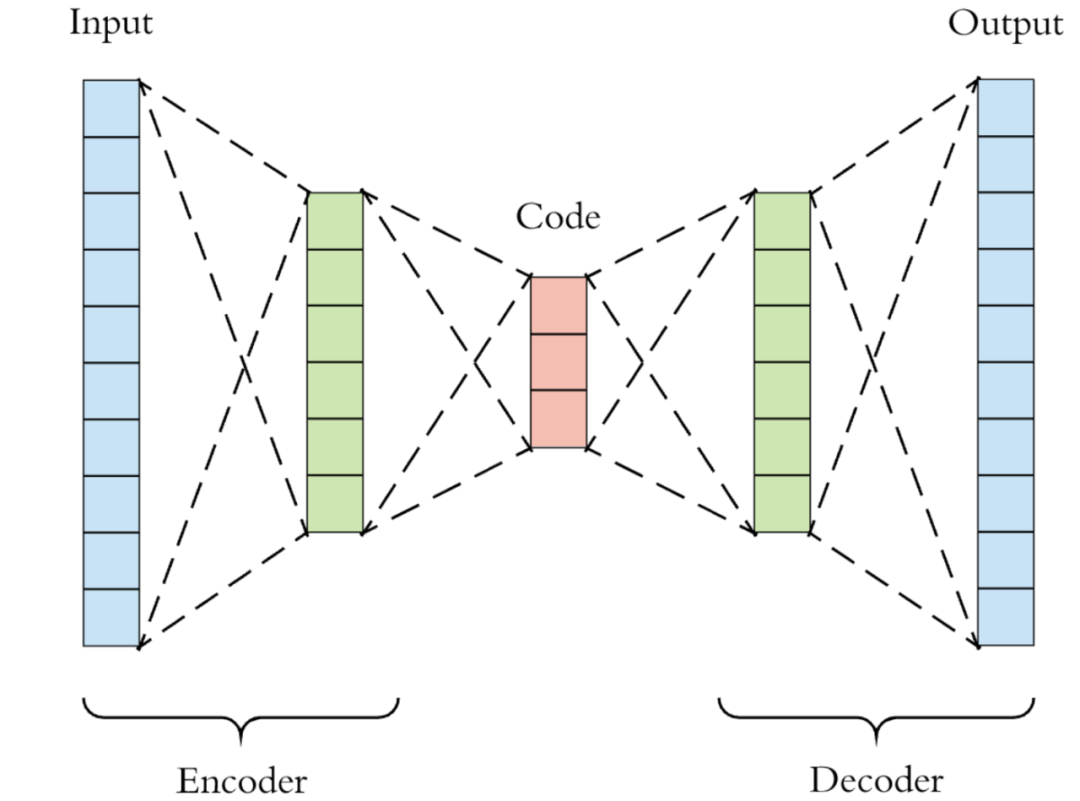
VAEs的网络结构和 AutoEncoder(AE)一样，由两个网络构成，分别是 Encoder 和 Decoder 。非常自然地， 对应上述 , 而 对应上述 。VAEs只是在 AE 的基础上用了变分推断，这也是其名字的由来。下图是一个简单的VAEs示意图，实际情况中网络结构可能更加复杂。蓝色分别为输入和输出，绿色为 Encoder / Decoder 的中间层，红色为 Encoder 的输出，一般是一个维度很低的向量 (仅限于早期简单的 VAE)，它有不同的名字，比如 code、latent representation、latent vector、embedding或者 bottleneck。

2.4 VAEs与AE的关系

最原始的 AE 的目标函数是:

其被称为 reconstruction error, 其目的便是希望 近似于恒等变换，但是 的输出维度非常小 (可以用矩阵分解 SVD 或者 NMF 来类比)。这看上去与 VAEs 的目标函数完全不同，但实际上有很强的联系。

我们从 VAEs 的 reparameterization 讲起。由于直接定义 和 是不现实的，我们假设这两个分布都是 Gaussian. 我们可以进一步简化，假定 covariance matrix 都是对角矩阵。那么，VAEs 中的 和 只需要输出 Gaussian distribution 的 mean () 和 covariance matrix () 的对角线即可。在这种情况下， 和 的表达形式都十分简单。我们将 ELBO 的第一项写开：

由于 , 我们有 , 其中 ， 就是用一个标准正态分布先乘上标准差再加上均值。当我们假定 且 很小的时候，上式与 AE 的目标函数其实非常类似。而 ELBO 的第二项则可以被视为 regularization term, 使得 与 latent distribution 接近。因此，VAEs 的 ELBO 目标函数常常被理解为 reconstruction error + regularization, 或者说在 AE 的基础上增加了 regularization.

2.5 Beta-VAE

Beta-VAE 是 VAEs 的简单推广，但十分有效。我们刚刚提到 VAEs 在 AE 的基础上增加了 regularization 从而得到更好的效果，那么我们可以直接增加一个 regularization factor 进一步提升效果:

= 1 便对应的是原始 VAEs。在实际任务中，我们只需要把 当作 hyper-parameter 进行 fine tune 即可。人们也发现，当 = 2,4,8 的时候效果一般会更好一些，尤其是生成的样本边缘更清晰 (sharp)。

当然，我们可以从另一个角度理解 -VAE. 我们从 AE 出发，优化 likelihood:

但同时 regularize term:

将上述优化问题转化为 Lagrangian multiplier, 我们有

舍弃最后的 项，我们便得到了 -VAE 的目标函数。

3. 模型衡量指标

3.1 推荐系统的Recall@k

因为是离线计算的指标，所以计算的时候用模型计算召回topk，看有多少个被用户真实点击了，就是表示命中用户喜欢样本的比值。

那么这个 设置怎样比较好呢？其实各有各的好处，比如5–500可能都有，一般会小的大的都看。如果 比较小，比如recall@5能代表模型的精确度，含义是在召回的top5中命中正样本的概率，如果明显精确度提高了，那么这个指标会提升。如果 比较大，比如recall@500能代表模型的整体效果，可能这个召回渠道线上每次拉取的都是一个比较大的结果，那么在这个大的结果中只要能够命中，都有可能最终被精排模型排出去，所以能代表模型整体召回效果。

「思考这个问题：Recall@k和线上指标是否是正相关的呢？」

从理论角度分析，假设只有这一个召回渠道，那么指标就是完全正相关的。但是线上正常情况不会这么简单，可能会有多个召回渠道，当前召回要经过粗排，最终进入到精排模型里面的数目是不确定的，所以如果离线指标recall@k从0～线上最大召回都是有提升的，那么就一定是正相关的，所以可以分区间多算几个看，比如recall@5，recall@10，recall@50，recall@100，recall@500。

3.2 NDCG@K

归一化折损累计增益（Normalization discounted cumulative gain）常用于排序任务，NDCG考虑到排序列表中每个item的评分大小。

「（1）CG@k」

CG（cumulative gain）累计增益，可用于评价基于评分的推荐系统，列表前 项的计算过程如下：

这里的 是用户对第 个item的评分值。需注意的是CG的计算并没有考虑列表中item的顺序。

「（2）DCG@k」

DCG（discounted CG）折扣增益的计算引入了item顺序的因素，列表前 项的计算过程如下：

不难发现，DCG结果的取值范围为全体非负实数，仅给出一个DCG的值无法判断推荐算法的效果。

「（3）NDCG@k」

NDCG将DCG的结果归一化到 之间，且越接近于 ，算法的效果越好。NDCG的归一化系数是IDCG，即理想的完美DCG。IDCG计算的是按照用户评分从高到低排序的列表DCG值。

结果列表前 项NDCG的计算过程如下：

4. 关于VAEs的若干问题思考

4.1 AutoEncoder、DAE和VAE之间的区别与联系？为什么会有VAE的出现？

由于AutoEncoder通过神经网络来学习每个样本的唯一抽象表示，这会带来一个问题：当神经网络的参数复杂到一定程度时AutoEncoder很容易存在过拟合的风险。为了缓解经典AutoEncoder容易过拟合的问题，在传统AutoEncoder输入层加入随机噪声来增强模型的鲁棒性，即降噪自动编码。相比于自编码器，VAE更倾向于数据生成。只要训练好了Decoder，我们就可以从某一个标准正态分布生成数据作为解码器Decoder的输入，来生成类似的、但不完全相同于训练数据的新数据，也许是我们从来没见过的数据，作用类似GAN。

4.2 VAE和GAN都是生成式模型，VAE与GAN的区别与联系？

这个问题，网上有很多答案，这里我给一个知乎的讨论帖子，里面有很多优秀的回答：

• GAN 和 VAE 的本质区别是什么？为什么两者总是同时被提起？- 知乎 https://www.zhihu.com/question/317623081

4.3 VAEs的后验坍塌(Posterior Collapse)？GAN的模式坍塌(Mode Collapse)？

「（1）VAEs的后验坍塌(Posterior Collapse)？」

涉及两个网络的模型训练起来都不是很简单, GAN 如此，VAE 亦如此。VAE 容易出现一种被称为 posterior collapse 的问题，即 完全学不出来。这个问题至今也没有完全被解决。有一个十分有意思的尝试是基于 normalizing flow (NF) 的，即 是一个 NF 模型。由于 NF 能直接定义 density, 且表征能力至少比 Gaussian 好不少，因此基于 NF 的 VAE 效果会得到显著提升。

「（2）GAN的模式坍塌(Mode Collapse)？」

Mode collapse 是指 GAN 生成的样本单一，其认为满足某一分布的结果为 true，其他为 False。

4.4 VAEs为什么在推荐的召回侧效果好？

VAEs是生成式模型而不是Encode压缩，保证了信息的完整性，Latent Vector是一个分布，而不是固定的，使得隐含空间在相似样本上的差异更加平滑，从而提高模型的拟合能力，避免样本细微的变化带来的模型参数波动。

4.5 AUC是否能作为召回离线评估指标呢？

首先，AUC是代表模型的排序能力，因为在召回环节考虑所有推荐物品的顺序没有太大意义，所以不是一个好的评估指标。

其次，AUC高并不代表召回的好，因为我们往往采样的负样本都是easy的，这样召回模型的AUC一般都是偏高的（auc=0.8+/0.9+都是有可能的）。实际上好的召回可能AUC低一些，但是会召回出更符合真实分布的内容，实际工作中AUC当作参考就好。

最后，召回模型AUC高也引出另一个召回的问题，就是如何挖掘hard负样本，以提升模型对于边界样本的区分能力，挖掘出好的hard负样本，也能减缓召回模型AUC过高的问题。

4.6 AUC和线上优化指标正相关嘛？

不相关。我们先从AUC的计算说起，计算AUC需要知道每个item的label和score，score决定了最终出去的顺序，但是这里的顺序只是召回环节的顺序，而召回后面还有模型排序，甚至中间可能还有粗排，所以最终用户看到的排序是精排模型的打分，和召回的分可能没有关系，甚至可能是相反的。所以说AUC在这里意义不太大，「那么AUC是否可以作为一个参考指标呢？」

答案是依然意义不大，因为召回的目的是把用户可能会喜欢的召回出来，最终顺序反而不是重要的，因为这里的顺序决定不了什么。反而召回结果中那些能进入到排序，以及推荐出去那些用户点击了的更重要。「那么有没有可能AUC是可以作为参考的呢？」

当召回层模型和排序侧使用相同的模型的时候，有参考价值，比如万能的FM模型，假设召回和排序用相同的，那么召回侧的顺序和精排模型侧排序是一样的，这样AUC就和线上指标完全相关了，可以作为离线评估效果指标。

5. 总结自编码器在推荐场景上的应用

• 《AutoRec: Autoencoders Meet Collaborative Filtering》WWW 2015，较早采用自编码器进行推荐的论文。
• 《Deep Collaborative Filtering via Marginalized Denoising Auto-encoder》 CIKM 2015，这篇论文是矩阵分解的DAE解法。
• 《Variational Autoencoders for Collaborative Filtering》WWW2018，详细信息已在本篇文章进行了介绍，且该论文在工业界有落地应用。
• 《Collaborative Denoising Auto-Encoders for Top-N Recommender Systems》发表在 the ninth ACM international conference on web search and data mining 2016，本文的亮点是可以在输入层加入用户侧的side information，该论文也在工业界有落地应用。

6. Reference

【1】变分自编码器 (VAE) Overview - Zhifeng的文章 - 知乎 https://zhuanlan.zhihu.com/p/420419446
【2】BERT模型精讲 - Microstrong的文章 - 知乎 https://zhuanlan.zhihu.com/p/150681502
【3】用于协同过滤的变分自编码器论文引介 - 听歌的小孩的文章 - 知乎 https://zhuanlan.zhihu.com/p/60330303
【4】基于自编码器的推荐系统论文引介 - Richard Gaole的文章 - 知乎 https://zhuanlan.zhihu.com/p/36241871
【5】Comprehensive Introduction to Autoencoders，地址：https://towardsdatascience.com/generating-images-with-autoencoders-77fd3a8dd368
【6】变分自编码器VAE：原来是这么一回事 | 附开源代码 - PaperWeekly的文章 - 知乎 https://zhuanlan.zhihu.com/p/34998569
【7】召回离线评估指标问题记录，地址：http://yougth.top/2020/10/15/%E5%8F%AC%E5%9B%9E%E7%A6%BB%E7%BA%BF%E8%AF%84%E4%BC%B0%E6%8C%87%E6%A0%87/
【8】推荐算法评价指标 - Noah的文章 - 知乎 https://zhuanlan.zhihu.com/p/359528909
【9】《变分自动编码器在协同过滤中的使用》做推荐召回 《Variational Autoencoders for Collaborative Filtering 》，地址：https://blog.csdn.net/xiewenbo/article/details/103724357
【10】论文解读:Variational Autoencoders for Collaborative Filtering.(WWW2018)，地址：https://blog.csdn.net/yfreedomliTHU/article/details/92093649