人工智能数学基础--不定积分2：利用换元法求不定积分-轻识

一、引言

在《人工智能数学基础–不定积分1：概念与性质》介绍了必须熟记的十三个基本积分公式及十一个扩展公式，利用这些公式以及不定积分的加法以及数乘性质，可以进行部分积分的计算，但非常有限，因此有必要进一步研究不定积分的计算。

本文介绍利用中间变量代换，将函数化为复合函数，利用复合函数求积分，相关方法称为换元积分法，简称换元法。

换元法分为两类，第一类是通过形如u=φ（x）变量代换后将函数化为某复合函数导数的形式，第二类是将x=ψ（t）进行变量代换，将代换后的函数化为某复合函数导数的形式。

二、第一类换元法

定理：设f(u)具有原函数，u=φ(x)可导，则有换元公式：

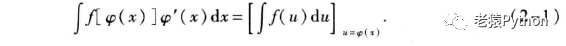
由此定理可见，虽然∫f[ φ(x]φ’(x)dx是一个整体记号，但从形式上看，可以认为是方便应用积分表进行计算的积分：∫f[φ(x]dφ(x)。

因此第一类换元法的核心思想是将∫f(x)dx形式的积分表达式中的f(x)dx化为φ(x)φ’(x)dx。

书中案例很多，挑3个有代表性稍微复杂的案例，以供大家理解：

一般地，对于积分∫f(ax+b)dx (a≠0)，总可作变换u=ax+b，把其化为：

一般地，对于sin2k+1x cosnx或sinnx cos2k+1x型的函数积分，总可以作变换u=sinx或u=cosx，求得结果。

类似地，对于tannx sec2kx或tan2k-1x secnx型的函数积分，总可以作变换u=tanx或u=secx，求得结果。

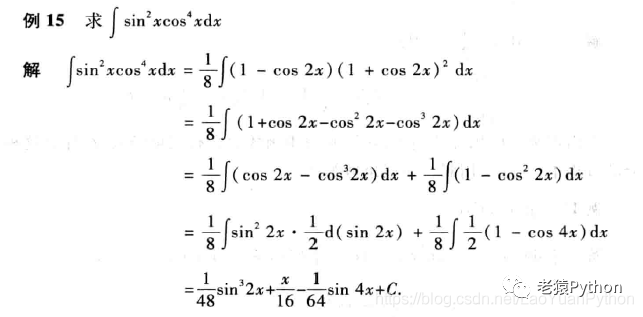
一般地，对于sinx的2m次方乘 cosx的2n次方型的函数积分，总可以利用三角恒等式sin^2x=(1-cos2x)/2或cos^2x=(1+cos2x)/2作变换化成cos2x的多项式，然后用上例的方法求得结果。类似地还可以利用和差化积或积化和差等三角恒等式进行变换。

三、第二类换元法

定理：设x=ψ(t)是单调的可导函数，并且ψ’(t)≠0，又设f[ψ(t)]ψ’(t)具有原函数，则有换元公式：

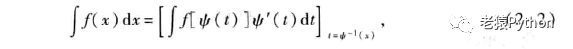
其中ψ-1(t)是x=ψ(t)的反函数。

说明：

这一公式的证明可以对公式（2-2）右边的被积函数求导即可证明；

与第一类换元公式的区别是需要用到一个中间变换，将x变为x为因变量其他引入参数如t为自变量的函数；

求出基于t的原函数后，要用t到x的反函数代换回去。

案例：

下面看个书中的案例：

注意：老猿在这里思考了一下，为什么能用x=asint？这是因为a^2 - x^2决定了x^2∈[0,a^2]，因此对于满足该要求的x都可以用asint来表达。

从上面的例子可以看出（受文字输入影响，下面的描述中根号用✓表示）：

类似地：

但具体解题时要分析被积函数的具体情况，选取尽可能简捷的代换，不要拘泥于上述的变量代换。

四、倒代换

除了上面介绍的2类代换外，还有一种用于消去分母中自变量的倒代换。

五、小结

本文介绍了三种换元法求不定积分的方法及案例，但具体解题时要分析被积函数的具体情况，选取尽可能简捷的代换，不要拘泥于特定的变量代换。

说明：

本文内容是老猿学习同济版高数的总结，有需要原教材电子版以及OpenCV、Python基础知识、、图像处理原理介绍相关电子资料，或对文章内有有疑问咨询的，请扫博客首页左边二维码加微信公号，根据加微信公号后的自动回复操作。

更多人工智能数学基础请参考专栏《人工智能数学基础》。