基于回溯算法的解题模板
回溯算法作为一种经典的有效的暴力搜索策略。其基本思想是搜索过程中沿着一条路径一直往前走,当探索到某一步时发现无法满足要求时,则退回到上一步选择另外一条路径继续往前搜索。对于许多大规模复杂问题而言,很多时候都可以通过回溯算法尝试解决

算法模板
结合LeetCode刷题经验,现对回溯算法的解题思路进行总结,并形成下面的伪代码模板。我们首先需要两个全局变量:result、state。前者用于保存最终搜索结果;后者用于记录搜索过程中的状态信息。故在程序入口getResult方法中首先需要通过init方法完成全局变量的初始化,最后直接返回全局变量result作为题解即可。而这期间通过search方法进行回溯搜索即可
search方法的最重要思路是根据当前状态等信息获取下一步搜索的可选择空间,即通过调用getAvailableList方法实现,然后遍历该可选择空间。具体地对于每个选择,先判断是否符合条件。如果符合,则说明可以选择它继续往前搜索。那么我们第1步先做出选择,包括对状态变量state的更新;第2步通过递归调用search方法实现所谓的一直往前搜索;第3步当递归调用结束返回时则说明已经当前搜索路径已经退回到上一步了,这个时候我们就需要撤销第1步做出的选择对状态变量的影响了。总而言之,回溯的关键就在于在递归搜索之前需要做出选择,而在递归搜索之后需要撤销选择
前面提到search方法会一直递归调用下去。那递归终止条件是什么呢?其实也很简单,第一种是发现不满足合法条件时直接return,即所谓的剪枝优化;第二种则是搜索成功,此时需要根据状态等信息将当前的搜索结果添加最终结果当中去
/**
* 回溯算法模板
*/
public static class Solution {
// 全局变量: 最终结果
private result;
// 全局变量: 当前搜索过程的状态信息
private state;
/**
* 入口
*/
public getResult(...) {
// Step 1: 初始化全局变量
init(...);
// Step 2: 回溯法搜索
search(...);
// Step 3: 直接返回搜索结果
return result;
}
/**
* 初始化全局变量
*/
private void init(...) {
result = ...
state = ...
}
/**
* 基于回溯算法的搜索
*/
private void search(...) {
// 剪枝
if( 不满足合法条件 ) {
return;
}
// 搜索成功
if( 满足搜索结束条件 ) {
// 根据当前状态信息, 更新result结果
...
return;
}
// 根据当前状态获取选择列表
availableList = getAvailableList(...);
// 遍历选择列表
for(int[] tempIndex : availableList) {
if( 判断当前选择 是否满足 合法条件 ) {
// 1. 做选择: 更新状态信息
...
// 2. 递归搜索下一步
search(...)
// 3. 撤销选择: 撤销对状态信息的修改操作
...
}
}
}
/**
* 根据当前状态获取选择列表
*/
private getAvailableList(...) {
...
}
}
实践
LeetCode: 17. 电话号码的字母组合
这里以 LeetCode 第17题 <电话号码的字母组合> 为具体示例来进行阐述
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。数字到字母的映射如下图(与电话按键相同),注意1不对应任何字母

示例 1:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = ""
输出:[]
示例 3:
输入:digits = "2"
输出:["a","b","c"]
按照模板则解法如下所示。由于本题在搜索过程中,任意一个搜索都是合法的,故不需要判断每次选择的合法性,直接按照 “做出选择-递归搜索下一个-撤销选择” 的思路进行处理即可
/**
* 回溯法
*/
public static class Solution {
/**
* 数字与字符的映射, key: 数字, value: 字母
*/
private static Map num2StringMap;
static {
num2StringMap = new HashMap<>();
num2StringMap.put('2', "abc");
num2StringMap.put('3', "def");
num2StringMap.put('4', "ghi");
num2StringMap.put('5', "jkl");
num2StringMap.put('6', "mno");
num2StringMap.put('7', "pqrs");
num2StringMap.put('8', "tuv");
num2StringMap.put('9', "wxyz");
}
/**
* 最终结果: 字母组合列表
*/
private List result;
/**
* 状态变量:当前搜索结果
*/
private StringBuilder sb;
public List letterCombinations(String digits) {
// 判空
if( digits==null || digits.length()==0 ) {
return Collections.emptyList();
}
// 初始化全局变量
init();
// 从第0个数开始搜索
search(digits, 0);
// 直接返回最终搜索结果
return result;
}
/**
* 初始化全局变量
*/
private void init() {
result = new LinkedList<>();
sb = new StringBuilder();
}
/**
* 回溯法递归搜索
* @param digits 待搜索数字
* @param index 搜索第index个数字
*/
private void search(String digits, int index) {
// 数字全部搜索结束
if( index == digits.length() ) {
// 将当前搜索结果加入最终结果集
result.add( sb.toString() );
return;
}
// 获取第index个数字的可选择字符
char num = digits.charAt(index);
String choice = getChooseList(num);
// 遍历可选择字符
for(char ch : choice.toCharArray() ) {
// 将当前字符加入搜索结果
sb.append( ch );
// 递归搜索下一个数字
search(digits, index+1);
// 将当前字符从搜索结果中移除, 即撤销所做出的选择, 以进行for循环的下一次遍历
sb.deleteCharAt( sb.length()-1 );
}
}
/**
* 当前数字的可选择字符
* @param ch
* @return
*/
private String getChooseList(char ch) {
return num2StringMap.get(ch);
}
}
LeetCode: 51. N皇后
这里以 LeetCode 第51题
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位
示例 1:
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如下图所示,4皇后问题存在两个不同的解法
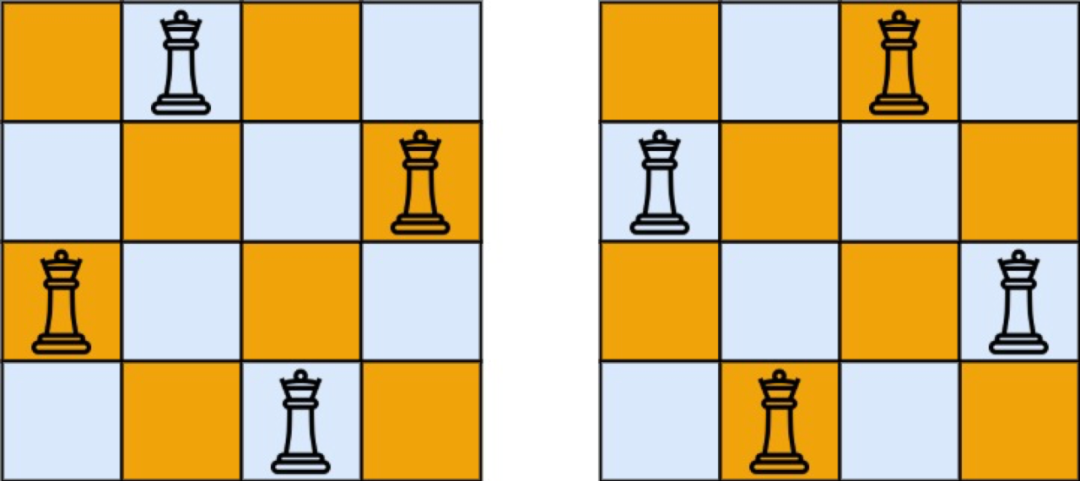
示例 2:
输入:n = 1
输出:[["Q"]]
按照模板则解法如下所示。本题中对于皇后的放置位置有一定要求,棋盘中的行、列、斜线不同同时放置两个皇后,故在遍历时通过isValid方法保证当前选择的合法
public static class Solution {
/**
* 最终结果:所有N皇后问题的解决方案
*/
private List> result;
/**
* 状态变量:n*n的棋盘布局, true: 表示相应网格放置了皇后, false: 表示相应网格未放置皇后
*/
private Boolean[][] board;
public List> solveNQueens(int n) {
init(n);
// 从第0行开始放置皇后
search(n, 0);
return result;
}
/**
* 全局变量初始化
* @param n
*/
private void init(int n) {
result = new LinkedList<>();
board = new Boolean[n][n];
for(int i=0; i Arrays.fill( board[i], false );
}
}
/**
* 递归法搜索
* @param n
* @param rowIndex 放置第rowIndex行的皇后
*/
private void search(int n, int rowIndex) {
// N个皇后全部放置完毕
if(rowIndex == n) {
// 将状态变量转换为棋盘布局, 并添加到最终结果当中
convert();
return;
}
for(int colIndex=0; colIndex if( isValid(rowIndex, colIndex) ) {
board[rowIndex][colIndex] = true;
search(n, rowIndex+1);
board[rowIndex][colIndex] = false;
}
}
}
/**
* 判断选择的合法性
* @param rowIndex
* @param colIndex
* @return
*/
private boolean isValid(int rowIndex, int colIndex) {
// 所在列不能有皇后
for(int i=0; i if( board[i][colIndex]) {
return false;
}
}
// 所在主斜线的左上方部分不能有皇后
for(int i=1;;i++) {
// 主斜线左上角的网格
int x1 = rowIndex - i;
int y1 = colIndex - i;
// 网格均不在棋盘范围内
if( x1<0 || y1<0 ) {
break;
}
// 存在包含皇后的网格
if( board[x1][y1] ) {
return false;
}
}
// 所在次斜线的右上方部分不能有皇后
for(int i=1;; i++) {
int x1 = rowIndex - i;
int y1 = colIndex + i;
if( x1<0 || y1>board.length-1 ) {
break;
}
if( board[x1][y1] ) {
return false;
}
}
return true;
}
/**
* 将状态变量转换为棋盘布局, 并添加到最终结果当中
*/
private void convert() {
List tempList = new LinkedList<>();
for(int i=0; i String rowStr = Arrays.stream( board[i] )
.map( e -> {
// true: 表示相应网格放置了皇后
if( e ) {
return "Q";
}
// false: 表示相应网格未放置皇后
return ".";
} )
.collect(Collectors.joining());
tempList.add( rowStr );
}
result.add( tempList );
}
}
剑指Offer(第2版): 12. 矩阵中的路径
这里以 LeetCode 的剑指Offer(第2版)题单中的第12题 <矩阵中的路径> 为具体示例来进行阐述
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用
例如,在下面的 3×4 的矩阵中包含单词 "ABCCED"(单词中的字母已标出)。
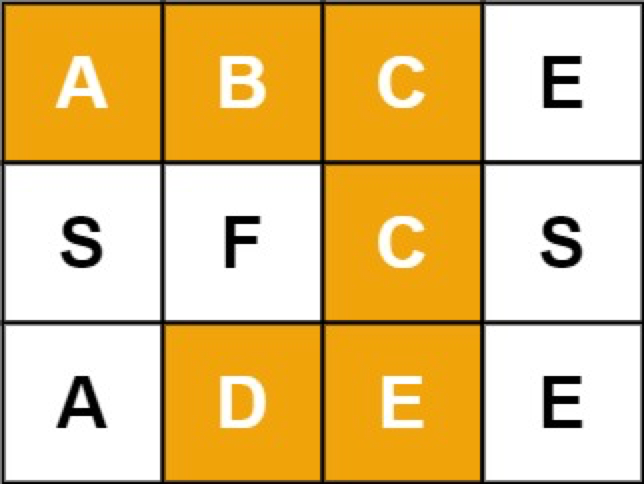
示例 1:
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
示例 2:
输入:board = [["a","b"],["c","d"]], word = "abcd"
输出:false
按照模板则解法如下所示。一方面本题每次的搜索路径为上、下、左、右这四个方向上未使用过的网络;另一方面本题只需判断能够搜索成功即可。所以当第一次搜索成功后,即可以不再进行搜索。故解法中加入了基于exist结果判断的剪枝优化
/**
* 回溯法
*/
public static class Solution {
/**
* 行数
*/
private int row;
/**
* 列数
*/
private int col;
/**
* 最终结果标记, true: 找到; false: 未找到
*/
private boolean exist;
/**
* 网格被访问状态标记, true: 该元素被访问; false: 该元素未被访问
*/
private boolean[][] usedArray;
public boolean exist(char[][] board, String word) {
if( board==null || board[0]==null || word==null || word=="" // 判空
|| board.length*board[0].length < word.length() ) { // 剪枝: 网格元素数小于字符串数量, 肯定搜索不到
return false;
}
// 初始化全局变量
init(board, word);
// 从字符串的第一个字符开始搜索
search(board, word, 0, 0, 0);
return exist;
}
/**
* 初始化全局变量
* @param board
* @param word
*/
public void init(char[][] board, String word) {
exist = false;
row = board.length;
col = board[0].length;
usedArray = new boolean[row][col];
}
/**
* 回溯法搜索
* @param board 网格
* @param word 字符串
* @param index 搜字符串的第index个字符
* @param i 网格元素的横坐标
* @param j 网格元素的纵坐标
*/
public void search(char[][] board, String word, int index, int i, int j) {
// 剪枝: 只要有一次搜索成功了即可结束搜索任务
if( exist ) {
// 剪枝
return;
} else if( index == word.length() ) {
// 搜索成功, 更新结果, 并结束
exist = true;
return;
}
// 获取选择空间
Set<int[]> indexSet = getAvailableIndexSet(index, i, j);
// 遍历选择空间
for(int[] tempIndex : indexSet) {
// 剪枝: 只要有一次搜索成功了即可结束搜索任务
if(exist) {
break;
}
int rowIndex = tempIndex[0];
int colIndex = tempIndex[1];
// 字符串的第index个元素搜索成功
if( board[rowIndex][colIndex] == word.charAt(index) ) {
// 将网格中相应的元素标记为 被访问状态
usedArray[rowIndex][colIndex] = true;
// 递归搜索字符串中的下一个元素
search( board, word, index+1, rowIndex, colIndex);
// 将网格中相应的元素标记为 未被访问状态, 即撤销所做出的选择, 以进行for循环的下一次遍历
usedArray[rowIndex][colIndex] = false;
}
}
}
/**
* 获取当前网格元素的可选择列表
* @param index
* @param i
* @param j
* @return
*/
public Set<int[]> getAvailableIndexSet(int index, int i, int j) {
// 自定义比较器: 当两个数组类型的元素, 如果数组中的内容均相同则视为同一元素
Set<int[]> indexSet = new TreeSet<>( (a1, a2) -> {
if( a1[0] == a2[0] && a1[1] == a2[1] ) {
return 0;
}
return 1;
});
// 搜索字符串第一个字符时, 则可选择的空间是整个网格
if( index == 0 ) {
for(int rowIndex=0; rowIndex for (int colIndex=0; colIndex int[] tempIndex = new int[]{rowIndex, colIndex};
indexSet.add( tempIndex );
}
}
return indexSet;
}
// 搜索字符串不是第一个字符时, 则可选择的空间是当前网络元素(i,j)的上、下、左、右这四个元素
int iMax = i+1 <= row-1 ? i+1 : row-1;
int iMin = i-1 >= 0 ? i-1 : 0;
int jMax = j+1 <= col-1 ? j+1 : col-1;
int jMin = j-1 >= 0 ? j-1 : 0;
indexSet.add( new int[]{iMin, j} );
indexSet.add( new int[]{iMax, j} );
indexSet.add( new int[]{i, jMin} );
indexSet.add( new int[]{i, jMax} );
// 选择空间中的元素需要移除掉已经被访问过的
indexSet.removeIf( tempIndex -> {
int rowIndex = tempIndex[0];
int colIndex = tempIndex[1];
return usedArray[rowIndex][colIndex];
} );
return indexSet;
}
}
剑指Offer(第2版): 13. 机器人的运动范围
这里以 LeetCode 的剑指Offer(第2版)题单中的第13题 <机器人的运动范围> 为具体示例来进行阐述
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
按照模板则解法如下所示。一方面本题每次的搜索路径为下、右这两个方向上未使用过的网络;另一方面本题要求的是统计机器人可以进入的方格总数。故每进入一个有效方格时,需要更新统计值,并将该方格标记为已访问过。但需要注意的是本题在回溯之后,即递归返回后不需要撤销所做出的选择。即不能再将之前已经访问的方格从已访问的状态撤销为未访问的状态。否则即会导致重复统计。换言之,在实际解题过程中不能生搬硬套解题模板。要善于理论联系实际、灵活应变。解题模板的作用在于总结经验、沉淀认知、减少解题的思维负担,它并不能完全取代、代替整个思考过程
class Solution {
/**
* 结果变量: 统计数
*/
private int result;
/**
* 状态变量: 方格访问标记
*/
private boolean[][] usedFlag;
/**
* 方向向量: 向右、向下
*/
private int[] dx = new int[]{0,1};
private int[] dy = new int[]{1,0};
public int movingCount(int m, int n, int k) {
if( k<0 ) {
return 0;
}
init(m, n);
search(k, 0, 0);
return result;
}
private void init(int m, int n) {
usedFlag = new boolean[m][n];
// 起点(0,0)是合法的
usedFlag[0][0] = true;
result = 1;
}
private void search(int k, int rowIndex, int colIndex) {
// 遍历可选路径
for(int i=0; i<2; i++) {
// 计算可选路径的坐标
int nextRowIndex = rowIndex + dx[i];
int nextColIndex = colIndex + dy[i];
// 满足搜索条件
if( nextRowIndex>=0 && nextRowIndex<=usedFlag.length-1
&& nextColIndex>=0 && nextColIndex<=usedFlag[0].length-1
&& calcSum(nextRowIndex, nextColIndex)<=k && !usedFlag[nextRowIndex][nextColIndex] ) {
// 更新计数值到结果变量
result++;
// 更新状态变量, 将其设置为已访问
usedFlag[nextRowIndex][nextColIndex] = true;
// 向下或向右继续搜索
search(k, nextRowIndex, nextColIndex);
}
}
}
/**
* 计算两个数的数位之和
* @param num1
* @param num2
* @return
*/
private int calcSum(int num1, int num2) {
int sum = 0;
while( num1!=0 ) {
sum += num1 % 10; // 取个位进行求和
num1 = num1 / 10; // 移除个位
}
while( num2!=0 ) {
sum += num2 % 10;
num2 = num2 / 10;
}
return sum;
}
}