图解:什么是 B+树 ? (查找篇)-轻识

来源：景禹

作者：景禹

前面谈了 B+树的基本概念，今日主要说一下 B+树的查找操作。

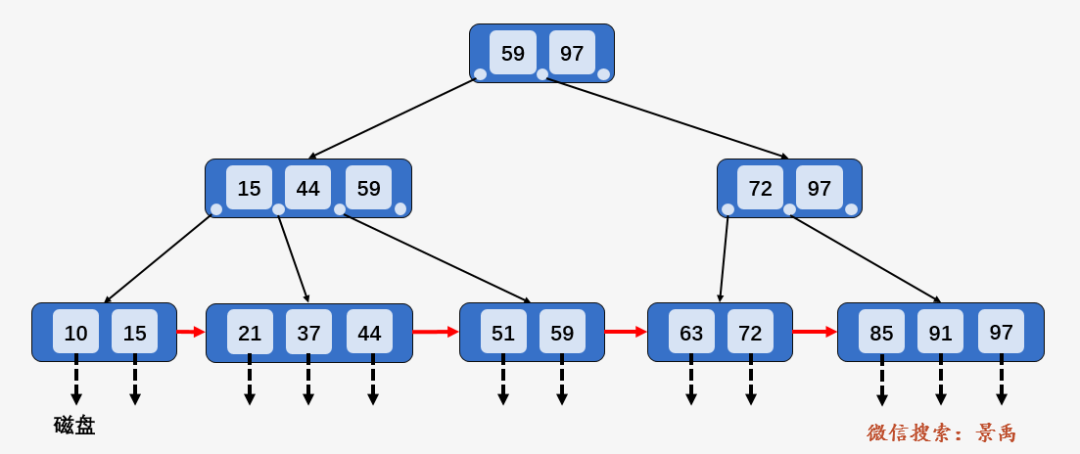
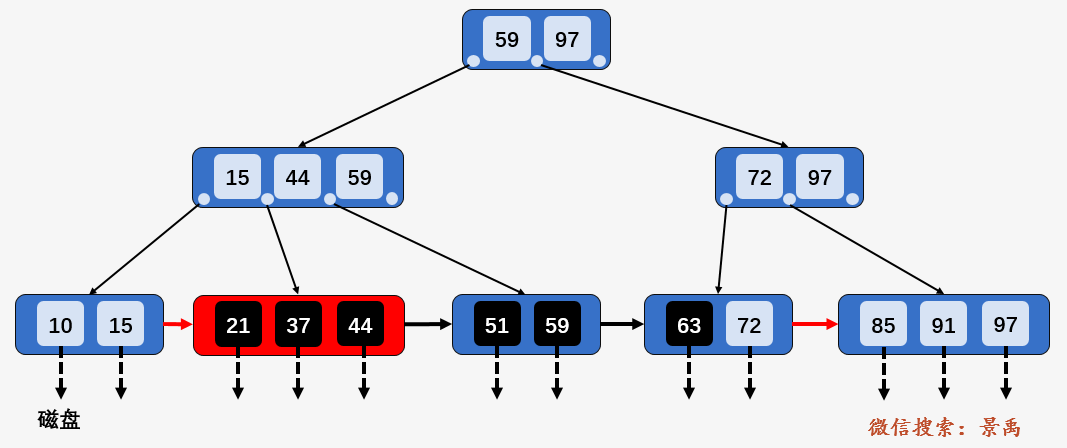
下面所有的查找操作都是在上面这颗 B+树上进行了，为此，我们先仔细观察一下这颗B+树（毫不隐瞒，这颗 B+树出自于严蔚敏老师的数据结构教材）。

第一点：B+树中的所有数据均保存在叶子结点，且根结点和内部结点均只是充当控制查找记录的媒介，并不代表数据本身，所有的内部结点元素都同时存在于子结点中，是子节点元素中是最大（或最小）元素。

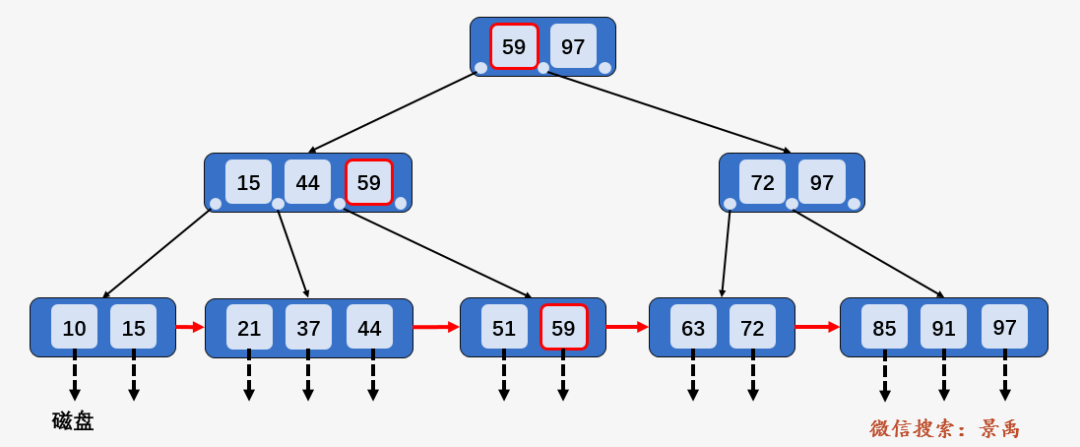
比如 B+ 树中的结点 59 （结点 15、44、97、72 类似），是其子结点 [15、44、59] 中的最大元素，也是叶子结点 [51、59] 中的最大元素。所有的数据 [10、15、21、37、44、51、59、63、72、85、91、97] 均保存在叶子结点之中，而根结点 [59、97] 及内部结点 [15、44、59] 与 [72、97] 均不是数据本身，只是充当控制查找记录的媒介。

需要注意的是，根结点的最大元素 97 是整颗 B+树当中最大的元素，无论之后在叶子结点中插入或删除多少元素，始终要保证最大元素在根结点当中，这个讲插入和删除时还会看到。

第二点：每一个叶子结点都有指向下一个叶子结点的指针，便捷之处就在于之后我们将看到的区间查找。

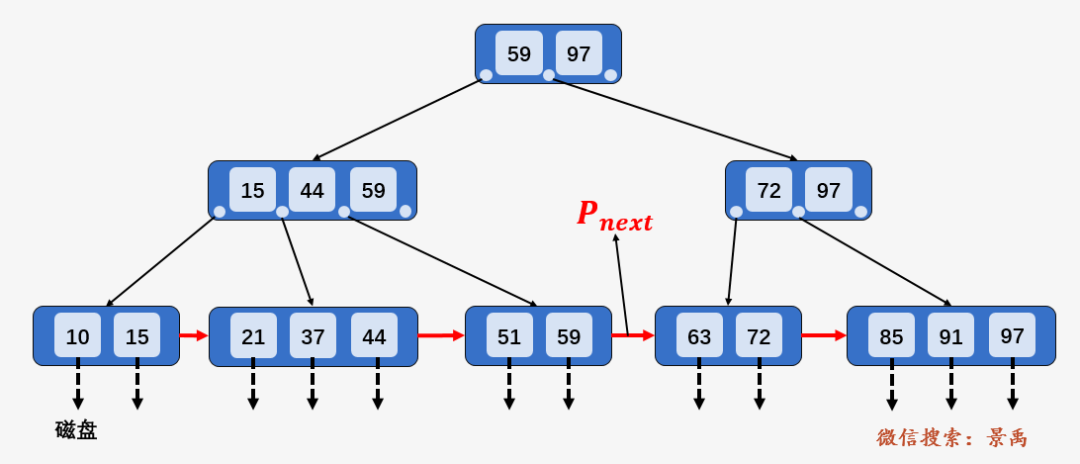
查询单个元素

我们以查询 59 为例进行说明。

第一次磁盘 I/O ：访问根结点 [59、97] ，发现 59 小于等于 [59、97] 中的 59 ，则访问根结点的第一个孩子结点。

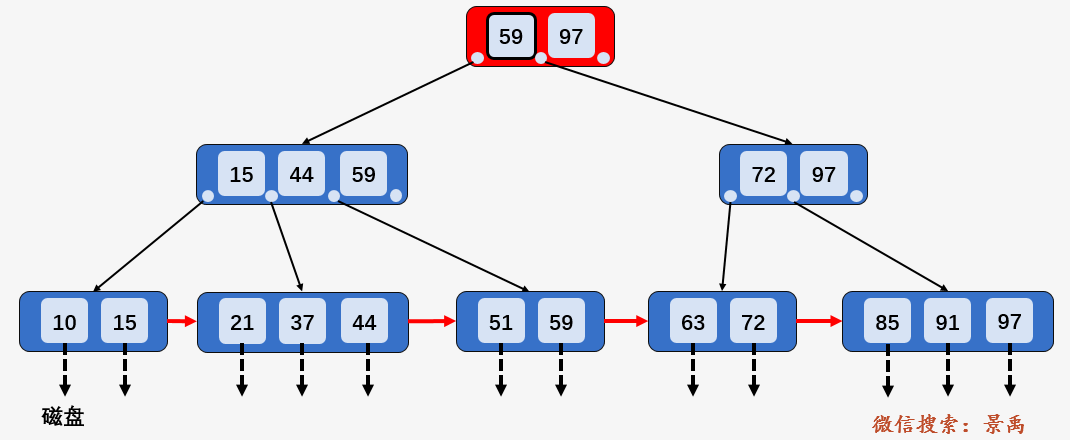
第二次磁盘 I/O : 访问结点 [15、44、59] ，发现 59 大于 44 且小于等于 59 ，则访问当前结点的第三个孩子结点 [51、59] .

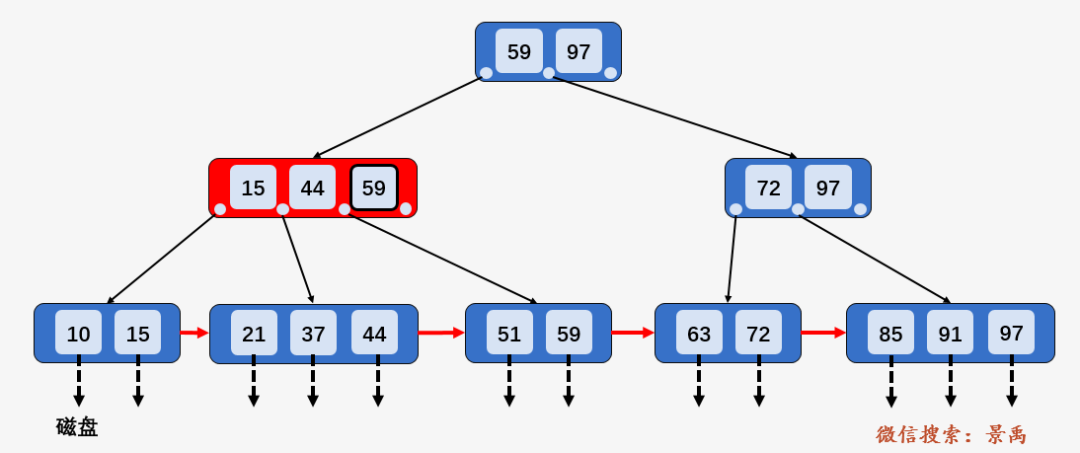
第三次磁盘 I/O ：访问叶子结点 [51、59] ，顺序遍历结点内部，找到要查找的元素 59 .

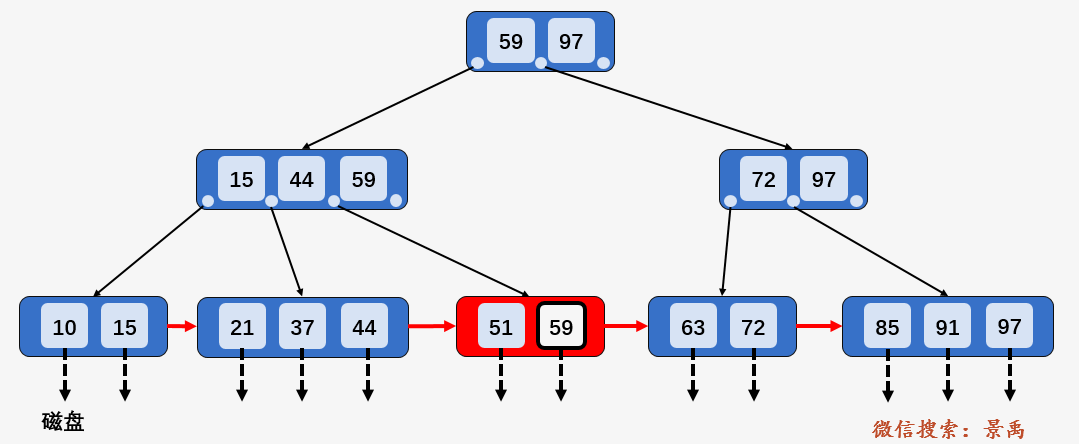
我想你已经注意到了和 B-树的区别，对于 B+树中单个元素的查找而言，每一个元素都有相同的磁盘 I/O操作次数，即使查询的元素出现在根结点中，但那只是一个充当控制查找记录的媒介，并不是数据本身，数据真正存在于叶子结点当中，所以 B+树中查找任何一个元素都要从根结点一直走到叶子结点才可以。

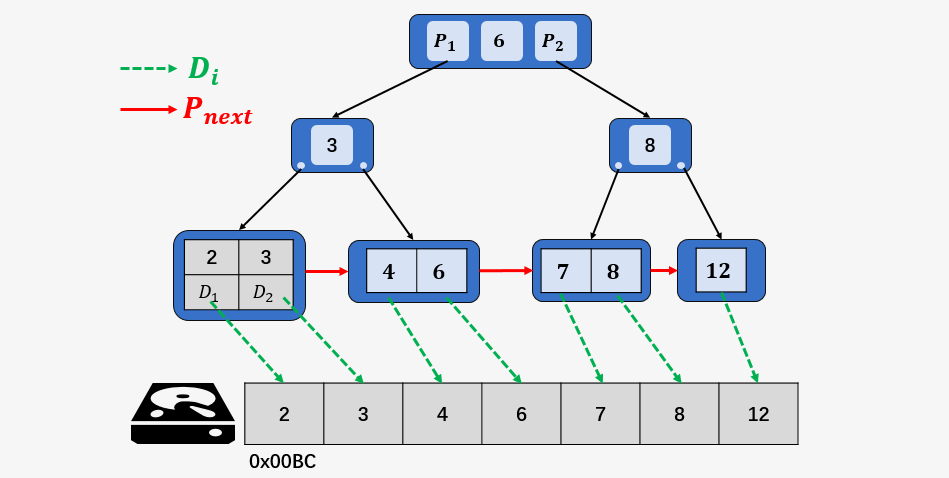
B+树的非叶子结点均不存储 Data (即，官方将其称为卫星数据) ，所以与 B-树相比，同样大小的磁盘页，B+树的非叶子结点可以存储更多的索引（关键字），这也就意味着在数据量相同的情况下，B+树的结构比 B-树更加 “矮胖”，查询时磁盘 I/O 次数会更少。

注意： B-树的查询性能并不稳定，对于根结点中关键字可能只有一次磁盘 I/O，而对于叶子结点中的关键字需要树的高度次磁盘 I/O 操作。

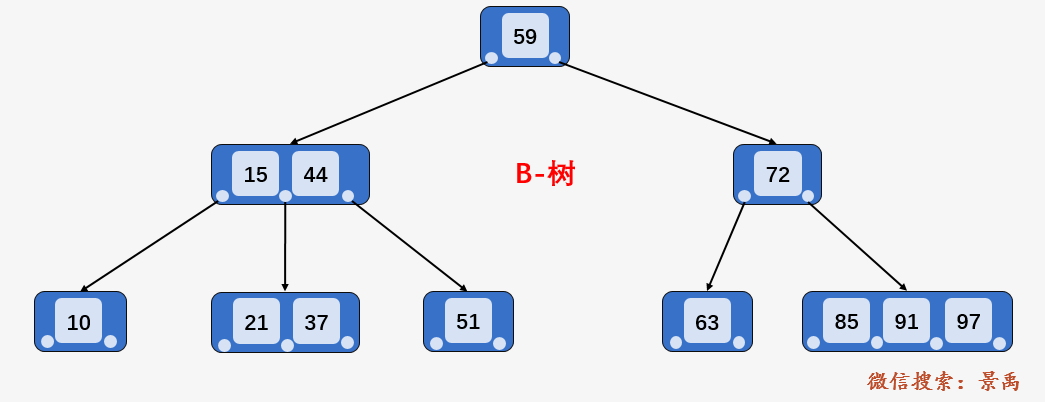
比如查找上图 B-树中的关键字 59 仅需要一次磁盘 I/O 操作，关键字 21 需要 3 次磁盘 I/O，关键字 72 需要 2 次磁盘 I/O.

B+树所有查询所有关键字的磁盘 I/O 的次数都是树的高度。

区间查询

为了更清楚地看到 B+树进行区间查询的优势，我们以查询下面的 B-树中大于等于21 ，小于等于63的关键字为例进行说明。

第一步：访问 B-树的根结点 [59] ，发现 21 比 59 小，则访问根结点的第一个孩子 [15、44] .

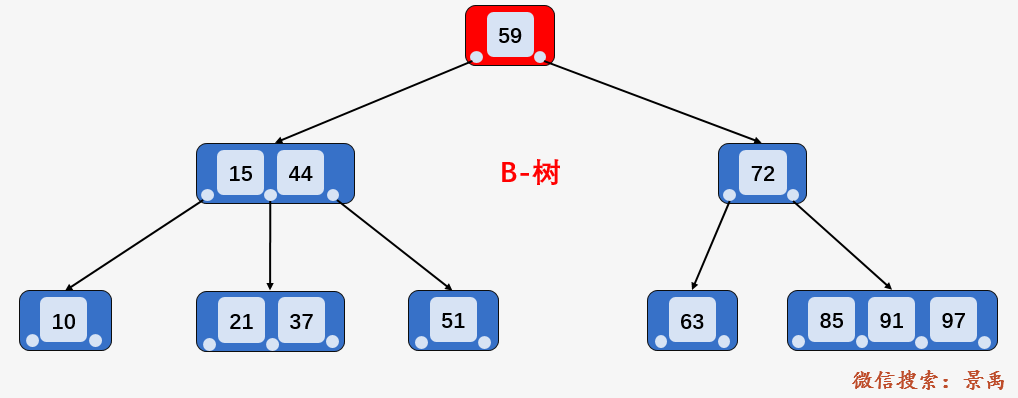
第二步：访问结点 [15、44] ，发现 21 大于 15 且小于 44 ，则访问当前结点的第二个孩子结点 [21、37] 。

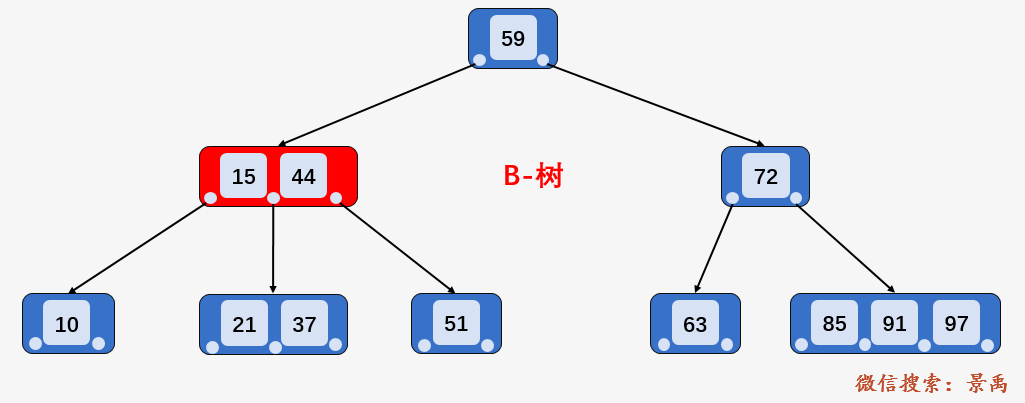
第三步：访问结点 [21、37] , 找到区间的左端点 21 ，然后从该关键字 21 开始，进行中序遍历，依次为关键字 37 、44、51、59，直到遍历到区间的右端点 63 为止，不考虑中序遍历过程的压栈和入栈操作，磁盘 I/O 次数多了 2次，即访问结点 72 和结点 63 并加载进内存。

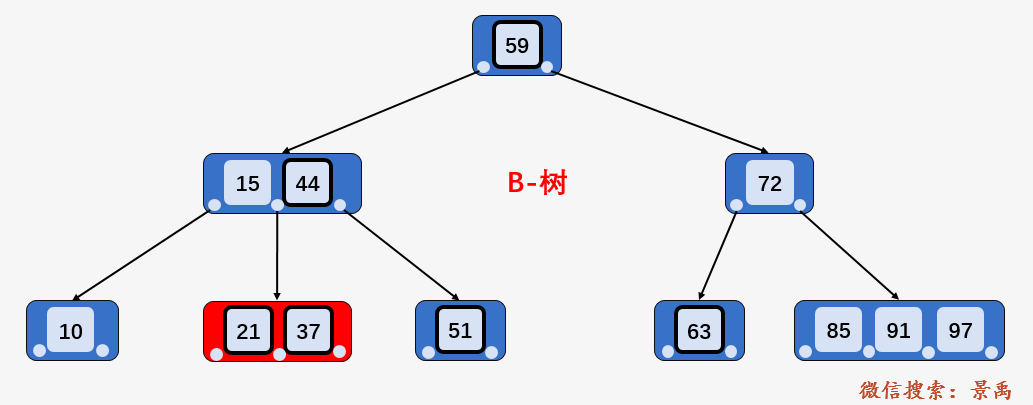
而 B+树进行区间查找，简直要舒服的不要不要的。同样是查找区间 [21,63] 之间的关键字。

第一步：访问根结点 [59、97] , 发现区间的左端点 21 小于 59，则访问第一个孩子结点 [15、44、59] .

第二步：访问结点 [15、44、59] ，发现 21 大于 15 且小于 44 ，则访问第二个孩子结点 [21、37，44] .

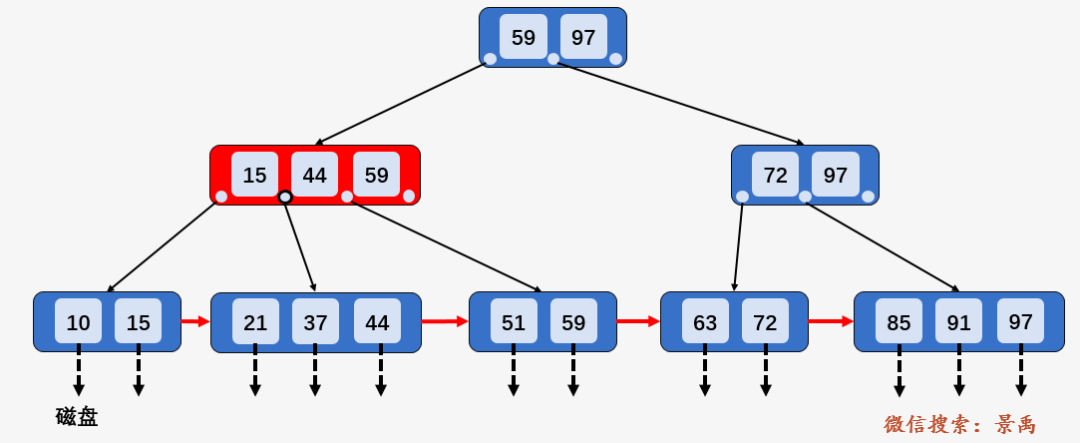
第三步：访问结点 [21、37，44] ，找到了左端点 21 ，此时 B+树的优越性就出来了，不再需要中序遍历，而是相当于单链表的遍历，直接从左端点 21 开始一直遍历到左端点 63 即可，没有任何额外的磁盘 I/O 操作。

综合来看 B+树的优势就是：

查找时磁盘 I/O 次数更少，因为 B+树的非叶子结点可以存储更多的关键字，数据量相同的情况下，B+树更加 “矮胖” ，效率更高。
B+树查询所有关键字的磁盘 I/O 次数都一样，查询效率稳定。
B+树进行区间查找时更加简便实用。

此外给大家推荐一篇博文 MySQL索引背后的数据结构及算法原理（http://blog.codinglabs.org/articles/theory-of-mysql-index.html），其中对于MySQL 索引为什么采用 B+树，以及InnoDB表为什么必须有主键，并且为什么推荐使用自增主键都有解释，需要的朋友可以自提，我就不再造轮子了。