图解：什么是AVL树？（删除总结篇）

来源：景禹

作者：景禹

上一篇文章讨论了平衡二叉树的插入操作，没有看的可以去看一下 图解：什么是AVL树？，有助于理解今天要讲的平衡二叉树的删除操作。

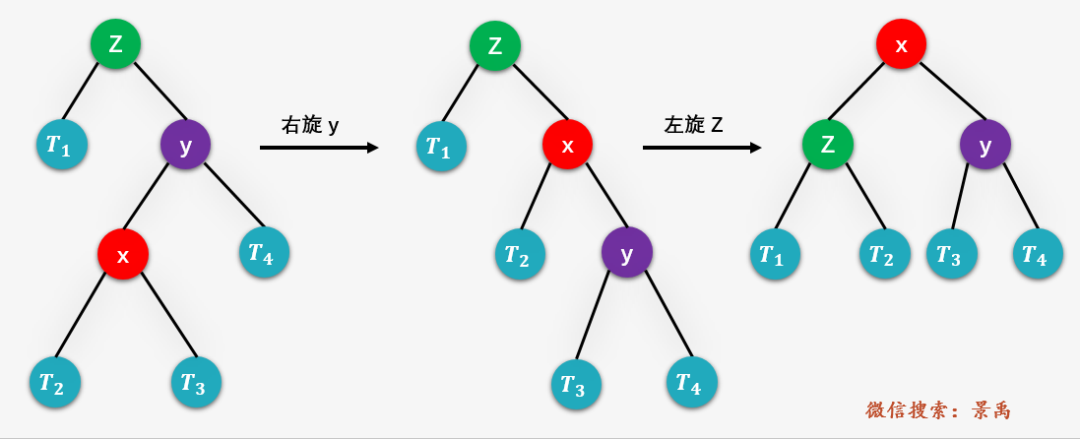
平衡二叉树的删除操作与插入操作类似，先执行标准的BST删除操作（可以参考文章 图解：什么是二叉排序树？ ），然后进行相应的平衡操作。而平衡操作最基本的两个步骤就是左旋和右旋，如下图所示：

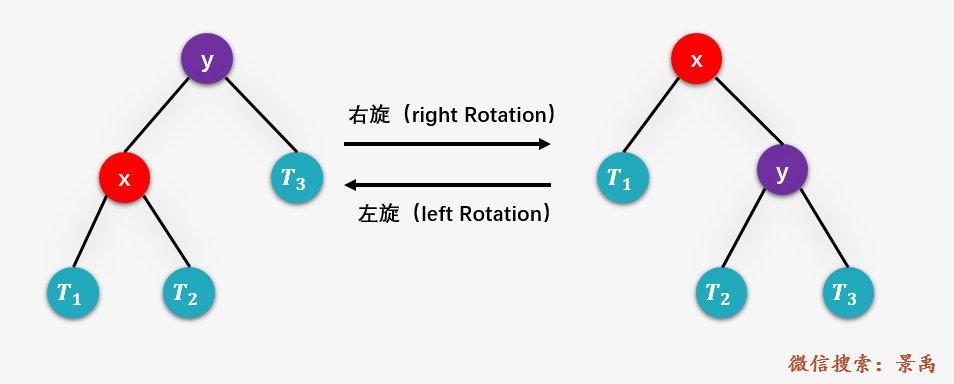
平衡二叉树的删除操作

与平衡二叉树的插入操作类似，我们以删除一个结点 为例进行说明平衡二叉树删除操作的具体算法步骤。

1. 对结点 执行标准的二叉排序树的删除操作；
2. 从结点 开始，向上回溯，找到第一个不平衡的结点（即平衡因子不是 -1，0或1的结点） ； 为结点 的高度最高的孩子结点； 是结点 的高度最高的孩子结点（ 这里一定注意和平衡二叉树插入操作区分开来，y不再是从w回溯到z的路径上z的孩子，x也不再是z的孙子这样的描述，一定要注意奥！！！ ）。
3. 然后对以 为根结点的子树进行平衡操作，其中 x、y、z 可以的位置有四种情况，BST删除操作之后的平衡操作也就处理以下四种情况：
• y 是 z 的左孩子，x 是 y 的左孩子 （Left Left ，LL )；
• y 是 z 的左孩子，x 是 y 的右孩子 （Left Right ，LR )；
• y 是 z 的右孩子，x 是 y 的右孩子 （Right Right ，RR )；
• y 是 z 的右孩子，x 是 y 的左孩子 （Right Right ，RL )；

这里的四种情况与插入操作一样，但需要注意的是，插入操作仅需要对以 z 为根的子树进行平衡操作；而平衡二叉树的删除操作就不一样，先对以 z 为根的子树进行平衡操作，之后可能需要对 z 的祖先结点进行平衡操作，向上回溯直到根结点。

第一种情况：LL

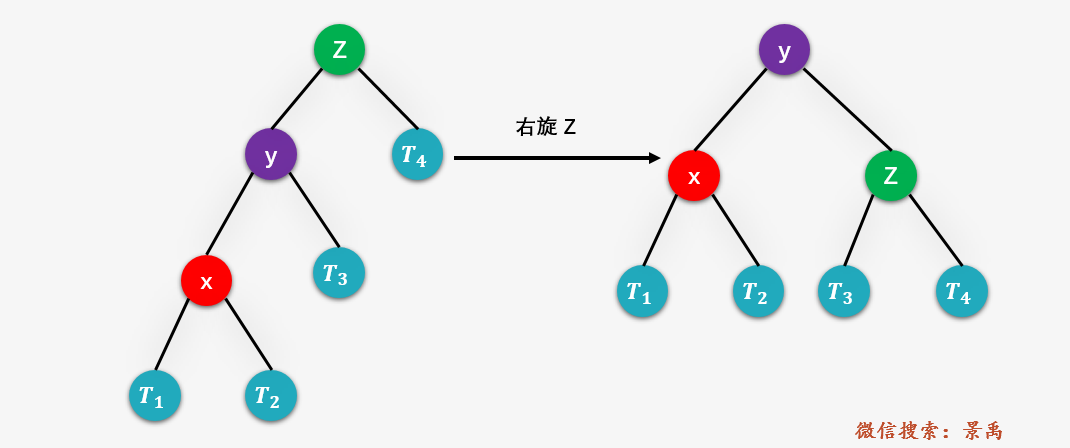
第二种情况：LR

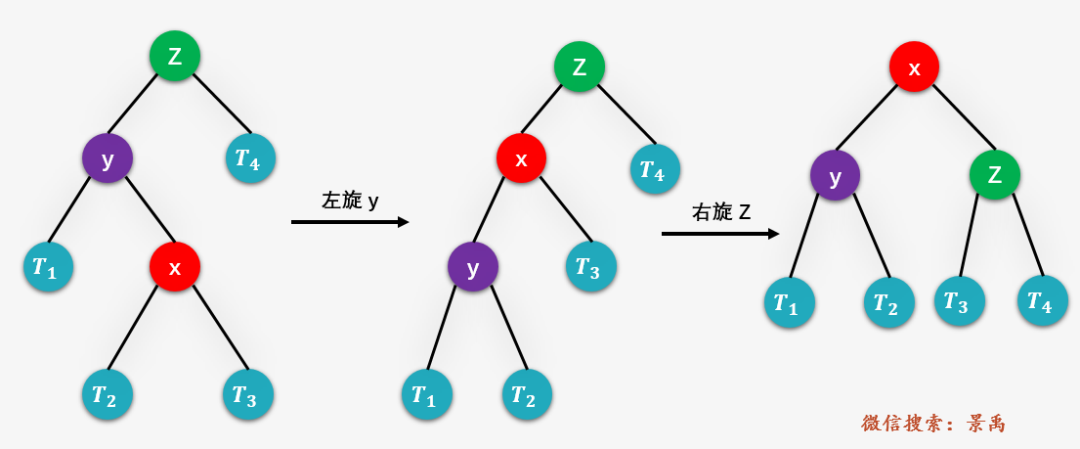
第三种情况：RR

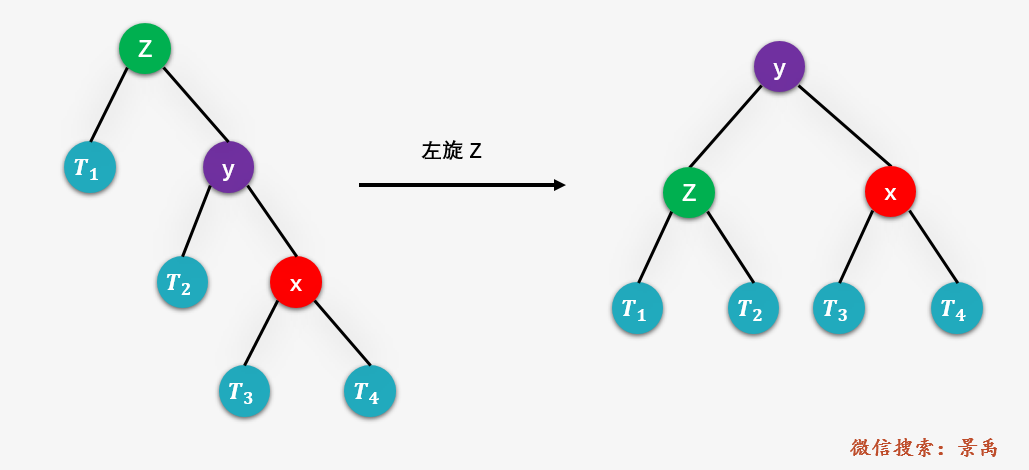
第四种情况：RL

举例说明

示例一：

我们已删除下图中的结点 32 为例进行说明。

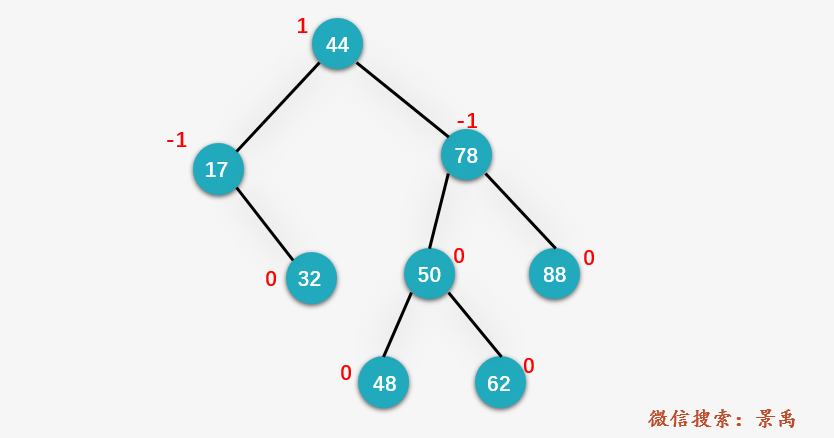
第一步：由于 32 结点为叶子结点，直接删除，并保存删除结点的父节点 17 。

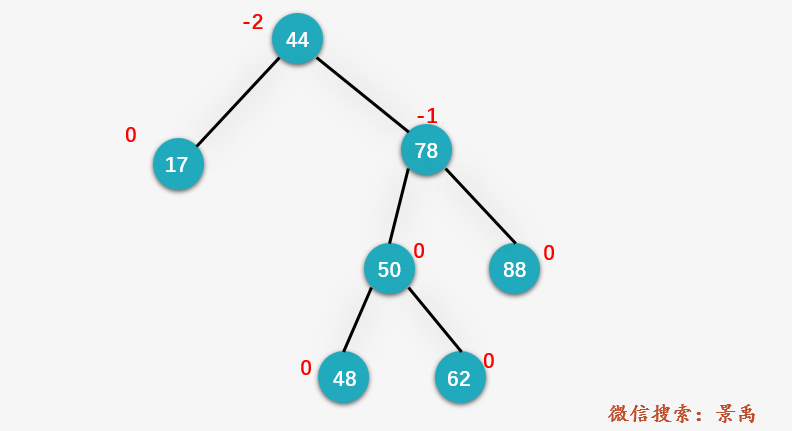第二步：从节点 17 向上回溯，找到第一个不平衡结点 44 ，并找到不平衡结点的左右孩子中深度最深的结点 78 （即 y ）；以及 y 的孩子结点当中深度最深的结点 50 （即 x ）。 发现为 RL 的情况。

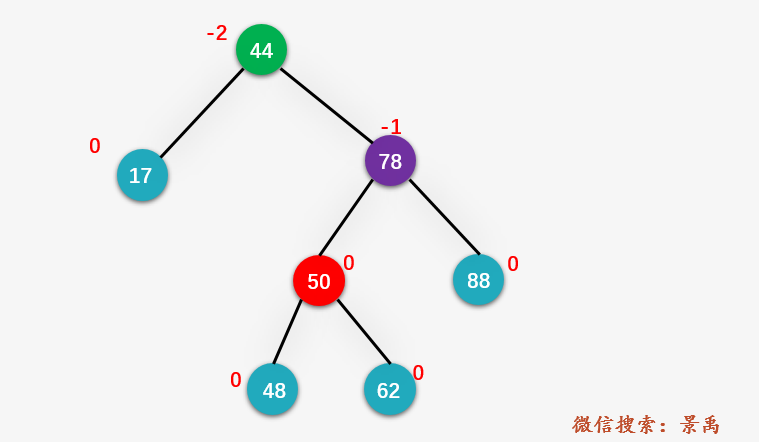
第三步：对结点 78 进行右旋操作

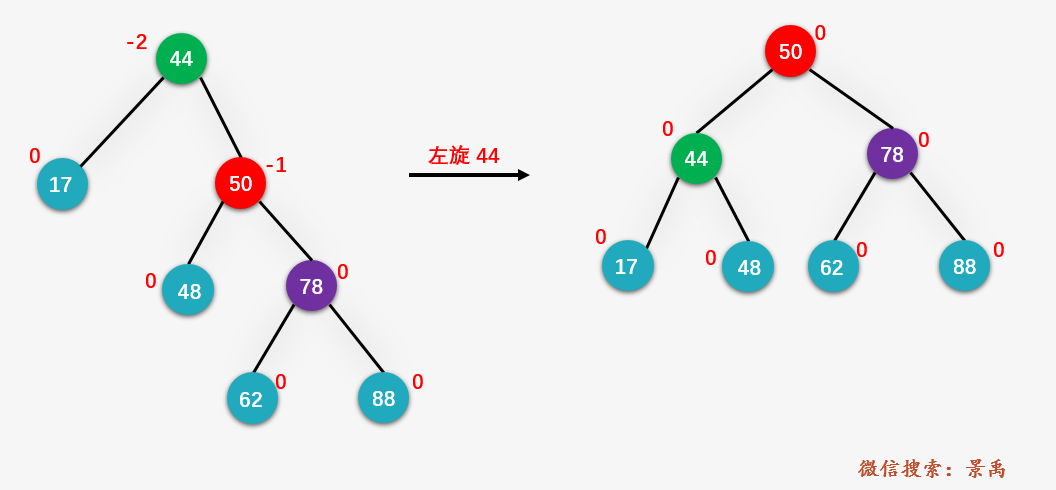
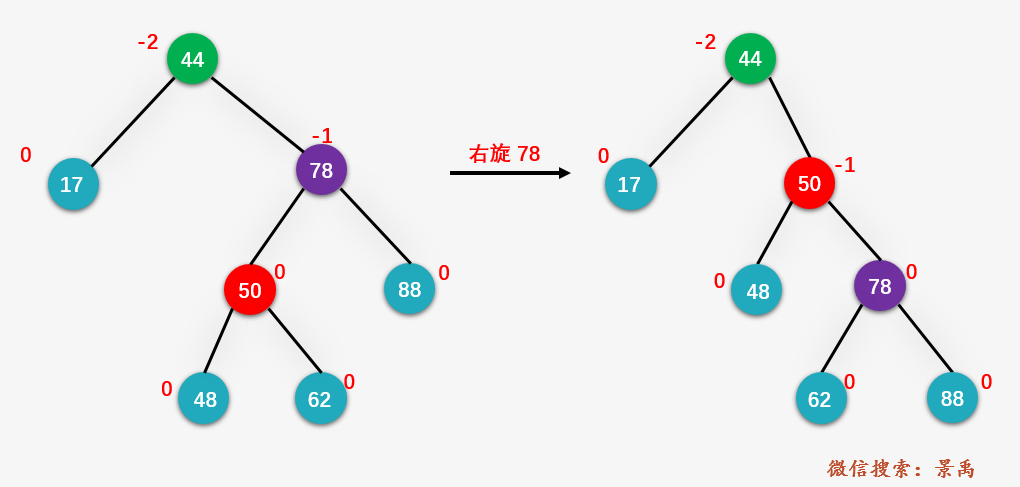第四步：对结点 44 进行左旋操作

示例二

我们以删除下图中的结点 80 为例进行说明。

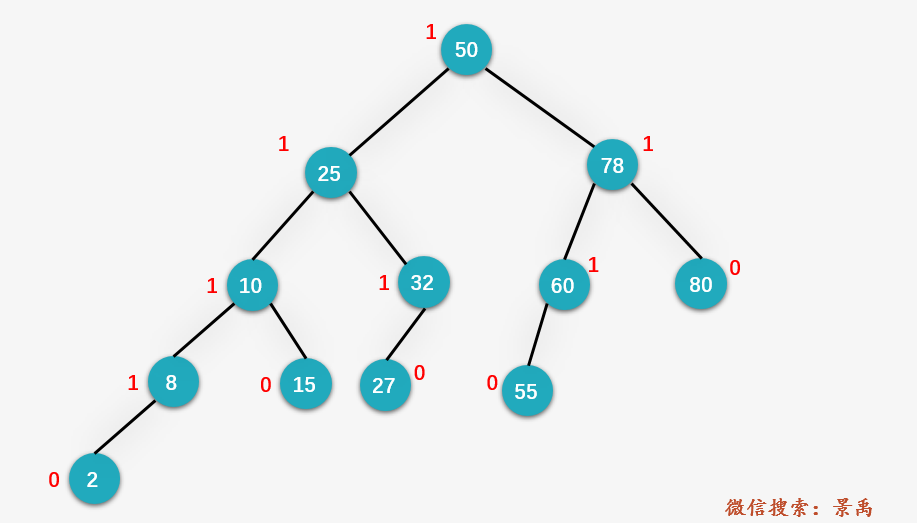
第一步，由于结点 80 为叶子结点，则直接删除，并保存结点 80 的父结点 78 。

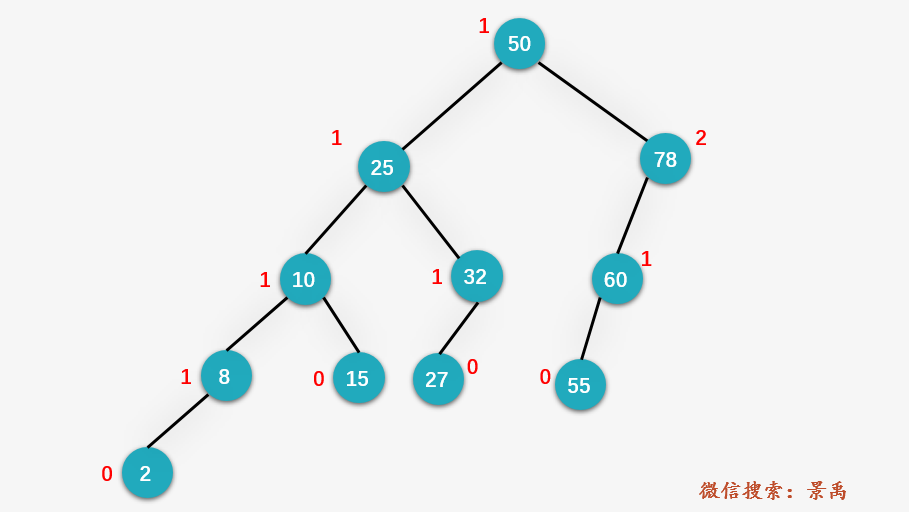
第二步：从结点 78 开始寻找第一个不平衡结点，发现就是结点 78 本身（即结点 z ），找到结点 78 深度最深的叶子结点 60 （即结点 y ），以及结点 y 的深度最深的叶结点 55 （即结点 x ）。即 LL 的情况。

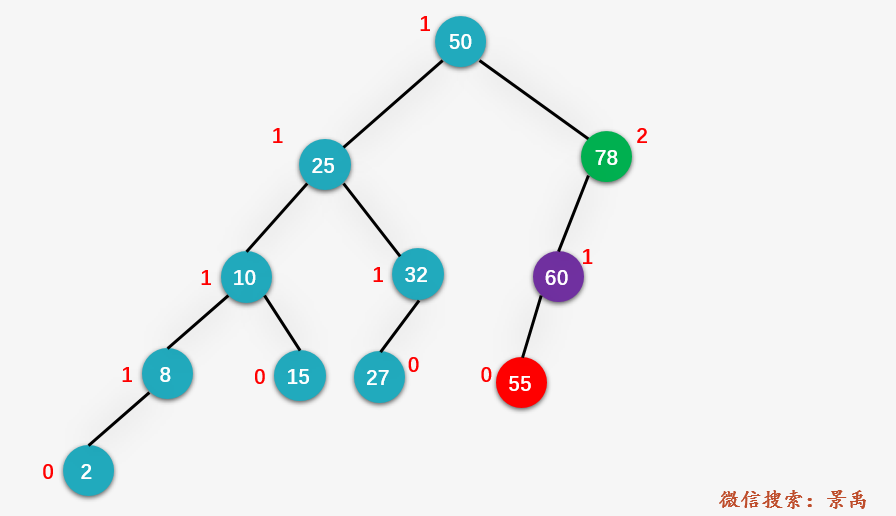
第三步：右旋结点 78

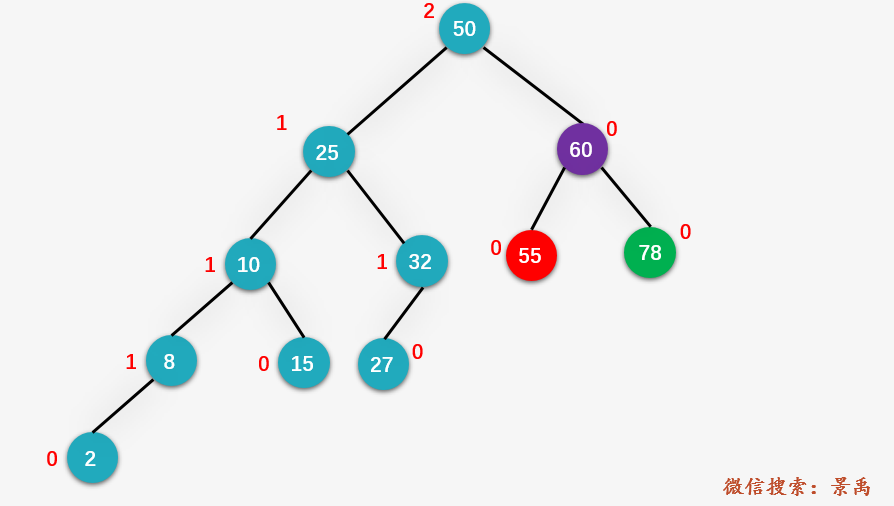
第四步：从旋转后的返回的新的根结点 60 向上回溯（这里就和平衡二叉树的插入操作有别了奥，平衡二叉树的插入操作仅对第一个不平衡结点的子树进行平衡操作，而AVL的删除需要不断地回溯，直到根结点平衡为止 ），判断是否还有不平衡结点，发现整棵树的根结点 50 为第一个不平衡结点，找到对应的 y 结点 25 和 x 结点 10 。同样是 LL 的情况。

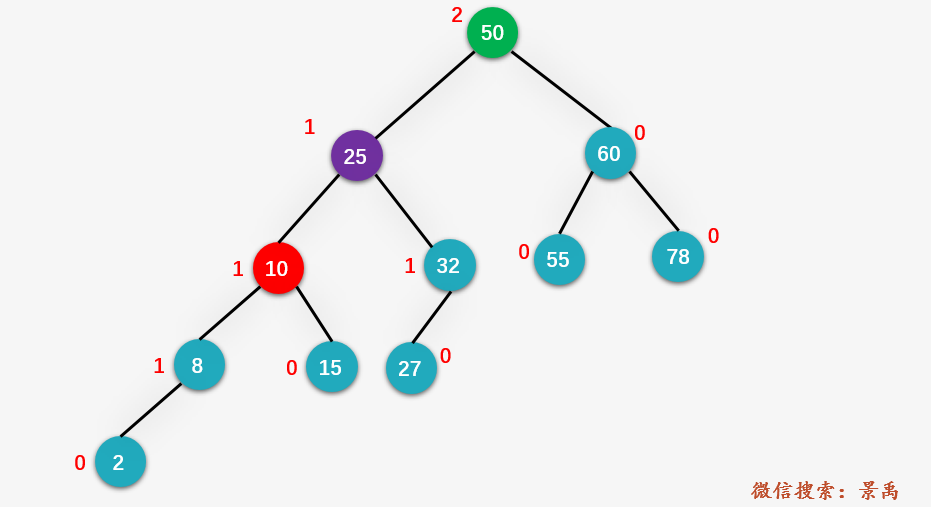
第五步：对 z 结点 50 进行右旋操作。

平衡二叉树的优缺点分析

优点

平衡二叉树的优点不言而喻，相对于二叉排序树（BST）而言，平衡二叉树避免了二叉排序树可能出现的最极端情况（斜树）问题，其平均查找的时间复杂度为 .

缺点

很遗憾，平衡二叉树为了保持平衡，动态进行插入和删除操作的代价也会增加。因此出现了后来的红黑树，过两天景禹自会抽时间讲解。

时间复杂度分析

左旋和右旋操作仅需要改变几个指针，时间复杂度为 ，更新结点的深度以及获得平衡因子仅需要常数时间，所以平衡二叉树AVL的删除操作的时间复杂度与二叉排序树BST的删除操作一样，均为 ，其中 h 为树的高度。由于AVL 树是平衡的，所以高度 ，因此，AVL 删除操作的时间复杂度为 .

平衡二叉树的删除操作实现

关于左旋与右旋操作，以及平衡因子的计算与之前讲的文章 图解：什么是AVL树？ 中的实现是一致的，我们直接看AVL删除操作的实现代码：

//返回删除指定结点后的平衡二叉树的根结点
struct Node* deleteNode(struct Node* root, int key) 
{ 
 // 步骤一: 标准的BST删除操作

 if (root == NULL) 
  return root; 

 //如果要删除的结点的key小于root->key
 //则表示该结点位于左子树当中，递归遍历左子树
 if ( key < root->key ) 
  root->left = deleteNode(root->left, key); 

 //如果要删除的结点的key大于root->key
 //则表示该结点位于右子树当中，递归遍历右子树
 else if( key > root->key ) 
  root->right = deleteNode(root->right, key); 

 //找到删除结点，进行删除操作
 else
 { 
  // 被删除结点只有一个孩子或者没有孩子，
  if( (root->left == NULL) || (root->right == NULL) ) 
  { 
   struct Node *temp = root->left ? root->left : 
           root->right; 

   // temp为空，左右孩子均为空
   if (temp == NULL) 
   { 
    temp = root; 
    root = NULL; 
   } 
   else // 仅有一个孩子
    *root = *temp; //拷贝非空孩子

   free(temp); 
  } 
  else
  { 
   // 被删除结点左右孩子都存在: 获取该结点的直接后继结点
   // 该结点右子树中最小的结点
   struct Node* temp = minValueNode(root->right); 

   // 将直接后继结点的值拷贝给删除结点
   root->key = temp->key; 

   // 删除其直接后继结点
   root->right = deleteNode(root->right, temp->key); 
  } 
 } 

 // 如果树中仅包含一个结点直接返回
 if (root == NULL) 
  return root; 

 //第二步: 更新当前结点的深度
 root->height = 1 + max(height(root->left), 
      height(root->right)); 

 // 第三步: 获取删除结点的平衡因子
 // 判断该结点是否平衡
 int balance = getBalance(root); 

 // 如果结点为不平衡结点，分以下四种情况处理

 // LL情况
 if (balance > 1 && getBalance(root->left) >= 0) 
  return rightRotate(root); 

 // LR情况
 if (balance > 1 && getBalance(root->left) < 0) 
 { 
  root->left = leftRotate(root->left); 
  return rightRotate(root); 
 } 

 // RR情况 
 if (balance < -1 && getBalance(root->right) <= 0) 
  return leftRotate(root); 

 // RL情况
 if (balance < -1 && getBalance(root->right) > 0) 
 { 
  root->right = rightRotate(root->right); 
  return leftRotate(root); 
 } 

 return root; 
} 

实战应用

题目描述

给定一个值 x ，返回一颗平衡二叉树中比 x 大的结点个数

输入输出示例

输入一个值 x  = 10 和下面的一颗平衡二叉树：

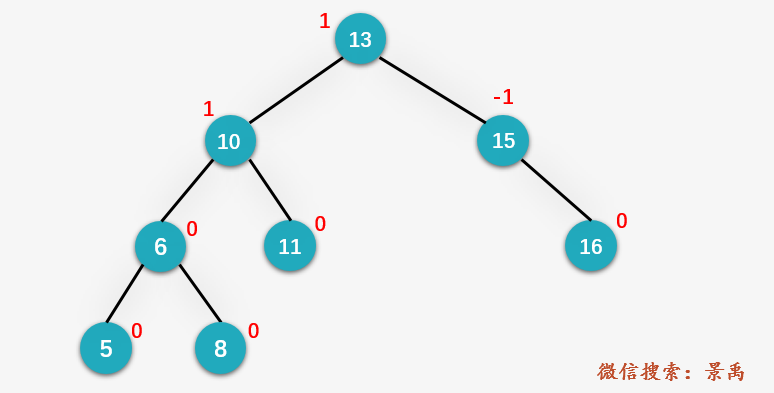
输出：4

解释：平衡二叉树中比结点10大有 11，13，14，16 ，共4个结点。

题目解析

1. 对于平衡二叉树中的每一个结点维护一个 desc 字段，用于保存每一个结点所包含的子孙结点的个数。比如示例中结点 10 的 desc 的值就等于 4，结点 10 的子孙结点包含 6、11、5、8 四个结点。
2. 计算大于给定结点的节点数目就可以通过遍历平衡二叉树获得了，具体包含以下三种情况：
• x 比当前遍历的结点的值大，我们则遍历当前结点的右孩子。
• x 比当前遍历的结点的值小，则大于指定结点的数目加上当前结点右孩子的 desc 加上 2 （加 2 是因为当前结点以及当前结点的右孩子都比指定的值 x 要大，当然是当前结点的右孩子存在的情况下）。具体操作是，判断当前结点的右孩子是否存在，如果存在则给大于 x 的结点数目加上当前结点的右孩子的 desc 并加2，否则 给大于 x 的结点数目加 1 ；然后将当前结点更新为其左孩子。
• 当 x 等于当前结点的值，判断 x 的右孩子是否存在，如果存在则将大于 x 的结点数目加上 x 的右孩子 desc ,然后再加上右孩子本身（即 1）；否则，右孩子不存在，则直接返回大于 x 的结点数目。

结点的定义中增加 desc 域：

struct Node { 
    int key; 
    struct Node* left, *right; 
    int height; 
    int desc; 
}; 

我们以查找示例网络中比结点 6 的结点数目为例讲解，比结点 6 的结点数目用 count 表示且初始化为 0；

第一步：访问根结点 13 ，发现结点 6 的值比 13 小，则 count 的值加上 13 的右孩子 15 的 desc=1 ，再加上结点 13 和 15 本身， count = desc + 2 = 3 .

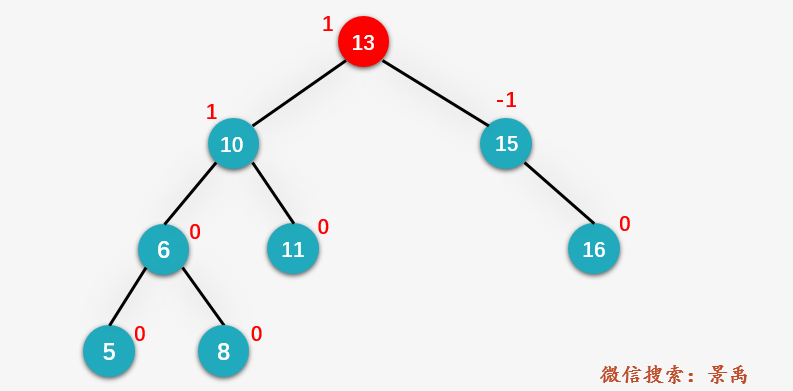
第二步：访问结点 13 的左孩子 10 ，6 < 10 ，则 count 的值应加上 10 的右孩子 11 的 desc 的值，再加 2，其中结点 11 的 desc 的值为0，故 count = 3 + 2 = 5 .

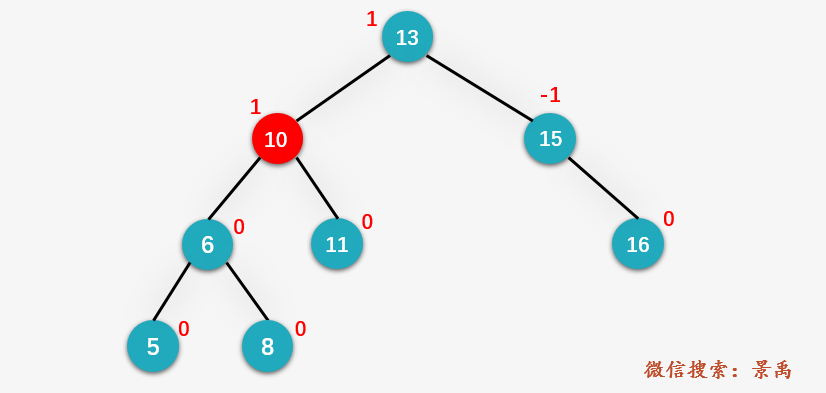
第三步：访问结点 10 的左孩子 6 ，发现与给定值相等，且结点 6 的右孩子存在，则 count 应加上结点 6 的右孩子 8 的 desc 以及结点 8 本身，即 count = 5 + 1 = 6 .

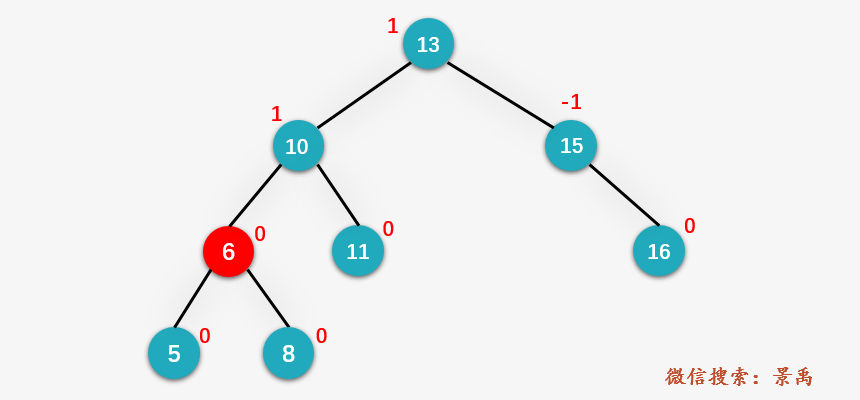
其实归结到最本质，整个过程就是利用了二叉排序树中，结点的右子树的值大于结点，左子树的值小于结点这样的特性。

那么该如何计算每一个结点的 desc 域呢？

1. 插入：每当插入一个新的结点，则给新插入结点的所有父结点的 desc 加 1 。当然相应的旋转操作也需要进行处理，稍后用图进行说明。
2. 删除操作：当删除一个结点，则将删除结点的所有祖先结点的 desc 减 1 。同样不论左旋还是右旋都需要进行处理。

还是以之前的左旋和右旋图说明 desc 值的相应变化：

左旋的情况下：

int val = (T2 != NULL) ? T2->desc : -1; 
x->desc = x->desc - (y->desc + 1) + (val + 1); 
y->desc = y->desc - (val + 1) + (x->desc + 1); 

当 不为空时，用一个临时变量 val 保存 的 desc 的值，否则将 val 赋值为 -1 。左旋操作后， x 的 desc 的值将等于其原来的值减去其原来的右孩子结点 y 的 desc ，再加上左旋之后其右孩子 的 desc + 1 ，即 val + 1 。

右旋的情况下：

int val = (T2 != NULL) ? T2->desc : -1; 
y->desc = y->desc - (x->desc + 1) + (val + 1); 
x->desc = x->desc - (val + 1) + (y->desc + 1); 

与左旋类似，当 不为空时，用一个临时变量 val 保存  的 desc 的值，否则将 val 赋值为 -1 。右旋操作之后，y 的值变为其之前的 desc j减去 x 的 desc+1 ，再加上 的 desc + 1 ，即 val+1 。而 x 的 desc 则变为其原来的 desc 的值减去 val+1 ，然后再加上旋转后的 y->desc + 1 。

有了上面的基础，我们可以一起先来看一下这道题目的左旋和右旋操作。

左右旋操作代码： 本质上与之前讲过的平衡二叉树插入和删除操作涉及的左旋与右旋一样，只是增加了上面的 desc 域的处理操作 （需要复习的就再看一遍代码，不需要的直接跳过）。

struct Node* rightRotate(struct Node* y) 
{ 
 struct Node* x = y->left; 
 struct Node* T2 = x->right; 

 //旋转操作，对着图看
 x->right = y; 
 y->left = T2; 

 // 高度更新
 y->height = max(height(y->left), height(y->right)) + 1; 
 x->height = max(height(x->left), height(x->right)) + 1; 

 // 更新desc 
 int val = (T2 != NULL) ? T2->desc : -1; 
 y->desc = y->desc - (x->desc + 1) + (val + 1); 
 x->desc = x->desc - (val + 1) + (y->desc + 1); 

 return x; 
} 


struct Node* leftRotate(struct Node* x) 
{ 
 struct Node* y = x->right; 
 struct Node* T2 = y->left; 

 //左旋 
 y->left = x; 
 x->right = T2; 

 //更新高度
 x->height = max(height(x->left), height(x->right)) + 1; 
 y->height = max(height(y->left), height(y->right)) + 1; 

 //更新 desc 
 int val = (T2 != NULL) ? T2->desc : -1; 
 x->desc = x->desc - (y->desc + 1) + (val + 1); 
 y->desc = y->desc - (val + 1) + (x->desc + 1); 

 return y; 
} 

获取结点 N 的平衡因子(复习）：

int getBalance(struct Node* N) 
{ 
 if (N == NULL) 
  return 0; 
 return height(N->left) - height(N->right); 
} 

平衡二叉树结点的插入操作（增加了对desc的处理，其他和之前讲的插入操作的实现一致）：

struct Node* insert(struct Node* node, int key) 
{ 
 /* 标准的BST的插入操作 */
 if (node == NULL) 
  return (newNode(key)); 

 if (key < node->key) { 
  node->left = insert(node->left, key); 
  node->desc++; //插入结点的左右祖先结点的desc++
 } 

 else if (key > node->key) { 
  node->right = insert(node->right, key); 
  node->desc++; 
 } 

 else // 二叉排序树中不允许插入相同的值
  return node; 

 /* 2. 更新祖先结点的高度 */
 node->height = 1 + max(height(node->left), 
      height(node->right)); 

 /* 3. 获取祖先结点的平衡因子，判断是否平衡*/
 int balance = getBalance(node); 

 // 结点不平衡，分一下四种情况处理

 // LL
 if (balance > 1 && key < node->left->key) 
  return rightRotate(node); 

 // RR 
 if (balance < -1 && key > node->right->key) 
  return leftRotate(node); 

 // LR
 if (balance > 1 && key > node->left->key) { 
  node->left = leftRotate(node->left); 
  return rightRotate(node); 
 } 

 // RL
 if (balance < -1 && key < node->right->key) { 
  node->right = rightRotate(node->right); 
  return leftRotate(node); 
 } 

 /*返回插入结点之后，树的根结点*/
 return node; 
} 

至于删除操作的修改代码，我就不在这里放了，需要的可以对上面的平衡二叉树删除操作的代码修改一下即可。我们主要看一下统计大于给定值 x 的结点个数的代码。

统计大于结点 x 的结点数目

int CountGreater(struct Node* root, int x) 
{ 
 int res = 0; 

 // 查找结点 x， 同时更新 res的值
 while (root != NULL) { 

  //保存当前结点的右孩子的desc
  //不为空则保存root->right-desc
  //否则保存 -1
  int desc = (root->right != NULL) ? 
    root->right->desc : -1; 

  //如果root的值大于x,则说明 x 位于左子树当中
  //res = res + 当且结点右孩子的desc + 2
  if (root->key > x) { 
   res = res + desc + 1 + 1; 
   root = root->left; 
  } //当root的值小于 x，则说明 x 位于右子树当中，继续查找
  else if (root->key < x) {
   root = root->right; 
  }
  else { //当相等时，res = res + x的右孩子的desc + 1.
   res = res + desc + 1; 
   break; 
  } 
 } 
 return res; 
}